多义图像合成算法研究

刘文兆 ， 湛永松， 石民勇

（1. 天津师范大学新闻传播学院，天津 300387；2. 中国传媒大学数字技术与艺术研发中心，北京 100024；3. 桂林电子科技大学计算机与控制学院，广西 桂林 541004）

近年来，合成具有多重含义的图像在计算机图像研究领域越来越受到关注[1-5]。多义图像是指以具有不同含义的两幅图像为目标，对其采取频域变换处理后融合成一幅图像，其在不同视角下可呈现出对应于目标图像的两种不同含义。产生不同的认知含义是基于人眼在固定视角下对不同频率具有不同敏感度的视觉特性[6]。通过改变图像不同频率下的内容，能使同一幅图像在不同视角下呈现不同视觉形象[2-4]。目前，多义图像在各种视觉广告、媒体、艺术、医疗、信息技术等领域具有广阔的应用前景。

Majaj[3]发现人眼对各类文字识别时在多个频率通道信息的选择上具有单一性，并由此将多个简单字母合成具有多重字母含义的图像，但其合成结果中多个字母干扰比较明显。Setlur[4]提出了合成不同频率下相互冲突的情感状态的面部图像算法，方法是先隔离不同面部表情的两幅图像中粗糙的低频成分和精细的高频成分，然后根据边缘检测进行图像分割和变形图像，合成具有多义情感的图像。虽然该方法可以保留较多的面部细节，但是由于对不同表情人脸进行区域分割后使用了变形算法，会产生介于不同表情之间的不自然的面部形态，导致其多义性不够明确和强烈。Schyns[2]使用混合图像的方法构造多义图像，Oliva[5]发展了该算法并取得了比较好的效果。其方法是将两幅图像分别进行高斯低、高通滤波，然后将两个滤波结果加权求和获得混合图像，其中的滤波操作在 Fourier变换下进行。该方法取得了视觉上较以往更好的多义效果，但由于在Fourier变换下无法确定相位信息，不能在合成过程中对结果图像进行局部调整。为获得理想的混合效果，需加大高通和低通截止频率之间的距离，使得合成图像丢失频带信息过多，导致结果图像变得模糊且色饱和度下降。

本文提出了一种基于小波变换的多义图像合成算法。小波变换具有精确表征图像的局部特征能力，通过对图像高频和低频成分分别制定融合规则以保留高、低频目标图像的特定信息，可实现局部特殊融合处理以及图像局部调整。用本文算法合成的图像能保留完整的频带信息，从而具有很高的色饱和度和清晰度，其视觉效果上的多义性也更为明确清晰。由于合成过程中不需变形处理，有效减少了人机交互操作，因此算法具有较高的合成效率。

1 小波变换

1.1 二维小波变换

小波变换具有多尺度多分辨率特点，能够在时域、频域同时表征信号特征。因此，二维小波变换已在目前成为图像处理的重要手段[7-9]。

1.2 Mallat快速算法[10]

STEPHANE G. MALLAT提出了二维信号多分辨率分解的小波快速算法，方法是：

若设H（低通）和G（高通）为2 个一维镜像滤波算子，其下标r和c分别对应于图像的行和列，则在尺度 j-1上有如下的Mallat分解公式

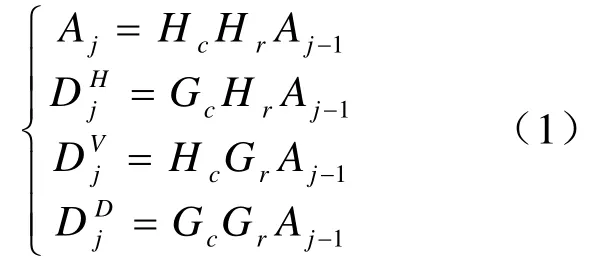
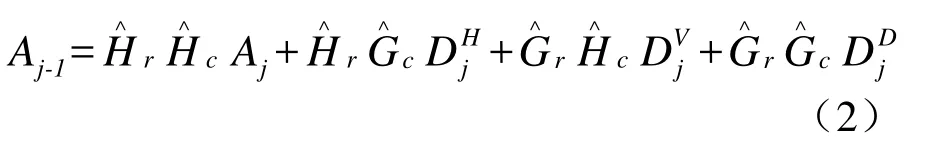
若对二维图像进行M级的小波分解，最终将有(3M＋1)个不同频带，其中有3M个高频带（细节成分）和一个低频带（近似图像）。

2 小波合成算法

2.1 算法概述

本文所提出的小波合成算法流程如图1所示。算法主要包括5个过程：小波分解、系数调整、高低频融合、图像重构、均值降噪。其中，高低频融合原则可采取预先提供的默认规则，此时可在人机交互的过程中加入局部滤波函数，从而对图像高低频系数进行局部调整之后融合。

融合前需要对两幅图像A、B进行预处理。根据素材具体条件及合成目的，将图像A、B的低频轮廓调整为一致（如图4，构造两幅低频主要轮廓接近的待合成图像）、冲突（如图8，构造强烈干扰高频的低频内容）或搭配（如图5、图7使低频与高频局部搭配一致，以加强高频效果）。对图像进行N阶M级的小波分解，分解深度M由图像尺寸和所需的多义观看视角决定，根据合成目的要求，制定融合规则。将图像A、B的小波低频分量融合为新的低频分量，此分量决定合成图像小视角观看时得到的形象；将A、B的高频系数融合为新高频系数，此分量决定合成图像大视角观看时得到的形象；之后用新系数重构图像。由于分解重构存在量化误差，可改变阶数N重复合成过程，对结果进行k次优选后均值降噪，得到最终的多义图像。

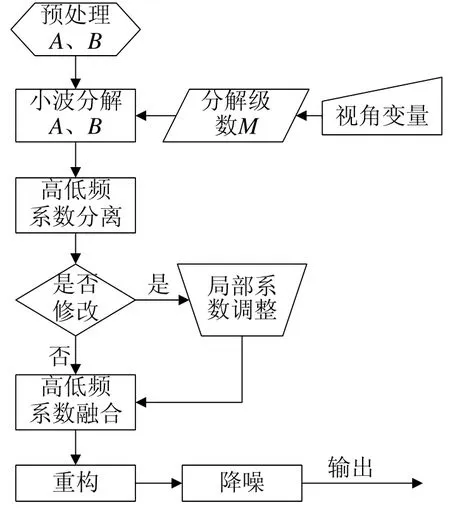
图1 多义图像合成算法流程图

2.2 融合方法

合成的目的是使结果图像在α视角（对应近距离观看或以大尺度显示）呈现图像A，β视角（对应远距离观看或以小尺度显示）呈现图像B，其中2＞α＞β＞0（单位：弧度）。首先根据用户给定的两个视距L1、L2（L2>L1）或视角α、β由式(3)计算合适的分解级数M，函数Ceil定义为取大于等于变量的最小整数

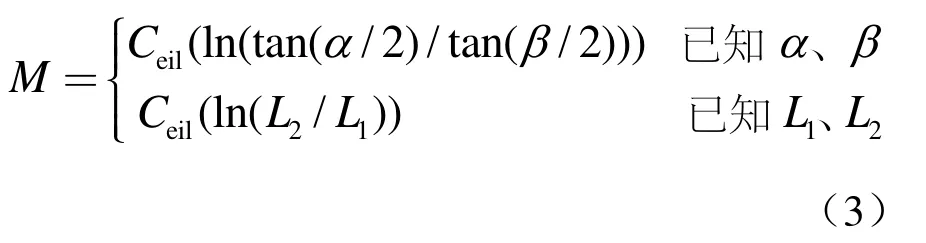
对图像A、B分别进行M级小波分解，并对第M级的低频和高频分别选定融合规则F，此时可在不同分解级上对低频和高频分量进行局部调整，融合后各分量如下

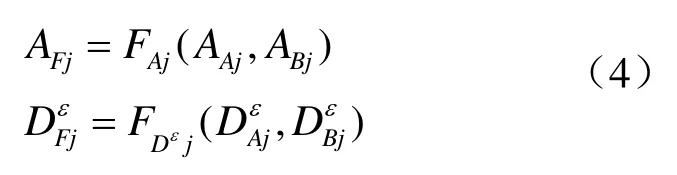
需要根据特定的素材图像及效果要求制定不同的融合规则，因此融合规则是合成的关键。为强化图像A或B的效果，给出可选的通用融合规则如下

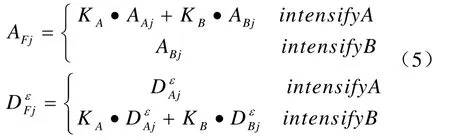
如需强调图像A的高频效果，FAj选择为两低频分量加权求和，KA、KB为用户输入的权值，FDj选择为取DAj；值得注意的是图像A的低频AAj权值越大，结果将越趋于重构图像A。若要强调图像B的低频，FAj选为取ABj，FDj选为两高频分量加权求和，通过改变B的高频权重，控制是否在重构过程中保留更多图像B的细节。

利用融合后的系数重构图象并保存结果。若需要对合成图像做局部调整，则在融合前对各分解系数进行局部滤波，然后重新融合重构。

2.3 误差处理

通过变换小波阶数 N自动重复 k次合成过程，对k个结果图象均值降噪后输出并保存。若不进行降噪，结果图像将看到轻微的噪波。噪波是由于DWT统一量化误差在对图像进行分解和重构的积分运算中被逐级放大造成的[9-10,14]，量化误差随小波阶数N增大而减小，噪波亦随之减小。若输入较大N值可一次就合成噪波较小的结果。图2(a)是合成图3(c)时，N=4的重构图像与均值图像3(c)的差值图像，由噪波的幅度可知降噪的必要性。图2(b)是做对齐预处理后与图4(e)的差值图像，其噪波幅度较图2(a)明显减小，图2(c)是经预处理后N=30时的差值图像，此时噪波已降到很小。

图2 不同N值的差值图像

3 实验及效果分析

下面分别通过合成多义人脸图像、猫脸纹理图像、冲突表情图像来比较不同算法的合成效果。为了客观比较本文算法与以往算法的效能，使用与文献[4-5]相同的素材进行合成比较。合成实验4给出了本文算法的其它2个效果。

3.1 人脸合成实验

人脸图例素材源于文献[5]。最终合成图像效果为大视角观看为端庄的女人（高频部分），小视角观看是愤怒的男人（低频部分）。

如图3(c)为A=I2和B=I1小波合成算法的结果。此处的融合原则取式(5)的强化B（权值KA=KB=0.5，M=4）。图4(e)为经过轮廓调整预处理后(A=I4，B=I3)在相同融合原则下得到的结果，算法以Daubechies小波变换进行M=4级分解，N选取4-30进行(k=27)均值降噪。图4的预处理只是为了比较处理效果，并非从艺术的角度对图像进行调整。图4(d)是在相同预处理下，融合原则选强化A（权值KA=0.3，KB=0.7）得到的结果。可以看出由于低频混合了I3、I4，使最终重构图像颜色发生变化，图4(d)的颜色介于I4和图4(e)之间。通过控制I4低频的权值可决定最终合成的颜色，但若融合I4的低频成分过高，将趋于完全重构I4。所以理想的方法是参照文献[11-13]在预处理阶段或合成之后重新映射图像的颜色以保证合成出希望的色彩。图4(f)是对融合系数进行局部调整后合成的结果，融合原则同图4(e)，目的是加强形象B的效果并消除B眉毛区域的低频对A形象的干扰（权值KA=0.3，KB=0.7）。

图3 I1、I2是目标图像，(a)、(b)文献[5]算法的结果，(c)小波合成算法的结果

图4 低频轮廓调整后的目标及合成图像

传统的客观评价融合图像方法多是对随机误差进行统计平均，虽计算简单易实现，但没有考虑人的视觉心里因素[6,15-16]，许多情况下并未反映人眼的视觉特性，不能和主观评价相一致。人对形象的认知经常建立在抽象的概念之上，很难用数学统计量标定。多义图像就是基于人眼的视觉特性对同一图像产生不同认知，因此主观评价比较直观和准确，容易操作。例如，通过视觉上比较图3(c)、图3(b)，可知图3(c)在两个视觉尺度上都更加清晰，色彩也更鲜明。视觉上比较图5(a)和图5(b)也可得到相同的结论。

文献[5]的算法给出的结果图3(a)低频图像突出，但是干扰高频，大视角时成为明显噪声。结果图3(b)效果稍好，它是加大滤波器高低频截止频率的差距后得到的，结果低频不够突出，小视角观看过于模糊。图3(a)和(b)的高频都不够突出，清晰度较差，对比度降低，合成图像损失原有高频图像的大量细节，图像看起来整体模糊，色彩饱和度低。

图4(e)利用本文算法很好的还原了图像的色彩饱和度和对比度，无论大视角还是小视角观看都很清晰，变换视角能够准确的识别出不同的人脸图像，多义特性非常突出和鲜明。图4(f)是素材经过轮廓对齐预处理并进行眼部调整得到的结果。由于素材A、B低频轮廓（对应低频近似图像中的高频）一致，即使低频进行了融合或替换，高频细节经小波重构仍可恢复，可看到十分清晰的面部细节，基本还原了素材图像的对比度。比较图4(e)和图3(c)可知：两个原始图像混合处理之前进行区域配准的预处理能有效解决低频干扰高频细节的问题。

3.2 纹理合成实验

图5(a)利用本文算法合成大视角观看具有猫脸纹理的女人像，观看时随视角变小，猫脸效果逐渐消失。由图5(a) 和图5(c)对比图5(b)和图5(d)可以明显看出，本文算法对比文献[5]合成的图像具有更高的色彩饱和度和对比度，无论大视角还是小视角观看都较文献[5]的结果清晰明亮，变换猫脸纹理的多义特性非常突出和鲜明。这里合成的目标图像A用遮蔽猫脸的女人像，B选原始女人像。参数为 Daubechies小波，权值KA=KB=0.5，M=3，N=4-30，K=27。

图5 猫脸纹理效果比较

3.3 表情合成实验

表情图例素材源于文献[4]。合成图像目的为大视角近看是愤怒的表情（高频部分），远看是高兴的表情（低频部分）。文献[4]的算法给出的结果如图6(c)，图像低频高兴的表情过于突出，干扰高频愤怒的表情成分难以识别，变形运算使结果图像更趋近于动作幅度大的高兴表情，面部动作幅度较小的愤怒表情因变形几乎完全破坏。图6(b)显示了本文算法突出愤怒表情的合成结果，如在大视角下观看愤怒表情的效果将更好。小视角下图6(a)和图6(b)高兴的表情都很清晰。参数为Daubechies小波，权值KA=0.25，KB=0.75，M=2，N=4-30，K=27。

3.4 效果实验

图7(a)给出一个高清晰的篮球纹理图片(1600×1200)，这里是缩小后的效果，以小尺度显示图7(b)可看到两个橘子。无论大小尺度都保持很高的色饱和度。融合规则选强化橘子，参数为Daubechies小波，权值KA=0.6，KB=0.4，M=6，N=4-30，K=27。

图8借助人类视觉思维一旦对容易组织起来的视觉内容形成概念，就很难打破再识别其它信息的特点[1]，当在低频部分构造容易识别的文字形象与高频冲突时，小视角低频内容诱导识别为其他文字，可以更好的屏蔽其它文字信息，实现信息遮蔽和隐藏。“不需要…信息”在大小视角都很清晰，“…隐私…”只有在大视角才可辨认。小视角只能识别“低频…内容”。参数为Daubechies小波，权值KA=0.7，KB=0.3，M=3。

图6 愤怒表情效果比较

图7 篮球与小尺度显示的橘子

图8 低频屏蔽高频文字内容

4 结 论

本文提出了一种基于小波变换的多义图像合成算法。与以往算法相比，该算法能够生成在色饱和度、对比度、低频清晰度、高频细节等多方面更理想的结果。合成可以对局部细节进行调整，主观视觉效果十分明显直观，适用于影视特效、视觉艺术、广告等商业领域。在未来的工作中，需要对提高算法效率进行研究。建立科学的多义图像合成效果的客观评定标准，对不同效果需求分类并给出相应高低频融合原则。此外，可将本文研究成果应用于连续的多义视频融合，并对更多层多义图像融合算法进行研究。

[1]OLIVA A, SCHYNS P. Coarse blobs or fine edges?evidence that information diagnosticity changes the perception of complex visual stimuli [J]. Cognitive Psychology, 1997, 34(1): 72-107.

[2]SCHYNS P, OLIVA A. Dr. Angry and Mr. Smile: when categorization flexibly modifies the perception of faces in rapid visual presentations [J]. Cognition, 1999,69: 243-265.

[3]MAJAJ N, PELLI D, KURSHAN P, et al. The role of spatial frequency channels in letter identification [J].Vision Research, 2002, 42: 1165-1184.

[4]SETLUR V, GOOCH B. Is that a smile?: gaze dependent facial expressions. In NPAR ’04:Proceedings of the 3rd International Symposium on Non-Photorealistic Animation and Rendering, ACM Press, New York, NY, USA, 2004: 79-151.

[5]OLIVA A, TOORALBA A, SCHYNS P G. Hybrid images ACM Transaction on graphics [J]. ACM Siggraph, 2006, 25(3): 527-530.

[6]BLAKEMORE C., CAMPBELL F W. On the existence of neurons in the human visual system selectively sensitive to the orientation and size of retinal images [J].Journal of Physiology (London), 1969, 203: 237-260.

[7]MALLAT S G. Multifrequency channel decompositions of images and wavelet models [J]. IEEE Trans.Acoust., Speech, Signal Processing, 1989, 37:2091-2110.

[8]Li H, MANJUNATH B S, MITRA S. Multisensor image fusion using the wavelet transform [J].Graphical Models and Image Processing, 1995, 57(5):235-245.

[9]DAVID A Y. Image merging and data fusion by means of the discrete two dimensional wavelet transform [J].J. Opt. Soc. A, 1995, 12(9): 1834-1841.

[10]MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11 (7): 674-693.

[11]REINHARD E, ASHIKHMIN M, GOOCH B, et al.Color transfer between images [J]. IEEE Computer Graphics and Applications, 2001, 21(5): 34-41.

[12]YU-WING TAI, JIAYA JIA, CHI-KEUNG TANG.Local color transfer via irobabilistic segmentation by expectation maximization [C]. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005: 747-754.

[13]NEUMANN L, NEUMANN A. Color style transfer techniques using hue, lightness and saturation histogram matching [C]. Computational Aestheticsin Graphics, Visualization and Imaging, 2005: 111-122.

[14]WATSON A B, YANGG Y, SOLOMON J A, et al.Visibility of wavelet quantization noise [J]. IEEE Trans.on Image Processing, 1997, 6: 1164-1175.

[15]HUGHES H C, NOZAWA G, KITTERLE F. Global precedence, spatial frequency channels, and the statistics of natural images [J]. Journal of Cognitive Neuroscience, 1996, 8(3): 197-230.

[16]CAMPBELL F W. The human eye as an optical filter [J].Proceedings of the IEEE, 1968, 56(6): 1009-1015.