基于模糊推理PID参数自整定在鼓风曝气控制中的应用
牛秦洲,张宗喜
(桂林理工大学 机械与控制工程学院,桂林 541004)
0 引言
目前污水处理方法中, 活性污泥法是应用最为广泛的处理方法之一,该工艺以生化反应池为核心处理单元。其中,生化反应池中溶解氧浓度的稳定控制是提高城市污水处理厂生化单元运行效率、保持污水处理厂出水水质达标、降低曝气系统能耗的必要条件。
目前国内污水处理厂对生化反应池鼓风曝气多采用人工控制、时间控制或者进水量比例控制,这些方法不仅消耗大量的人力、物力,而且造成电能的严重浪费。由于污水处理厂的进水水质和水量是变化的、随机的,常规PID控制方法,对系统模型精确性依赖强,其参数往往整定不良,性能欠佳,但是借助PID参数的在线模糊自整定,实时修改PID参数,就可确保系统在运行过程中始终处于优化状态。鼓风曝气过程采用基于模糊推理PID参数自整定技术,是污水处理设备智能化的核心单元技术,也是提高污水处理质量和降低能耗的关键技术。从污水处理设备的技术发展进程看,自动化、智能化是污水处理设备发展的必然趋势。
1 PID参数
1.1 PID参数对系统的影响
要改进PID控制的动态特性,必须研究PID调节参数Kp、Ki和Kd对系统动、静态性能的影响。
1)比例环节的作用是减少偏差,比例系数Kp增大可以加快响应速度,减小系统稳态误差,提高控制精度。过大会产生较大超调,导致系统不稳定;过小可减少系统的超调量,也会降低系统的调节精度,使系统的过渡过程时间延长。
2)积分环节用于消除系统静差,提高系统无差度,但会使系统响应速度变慢,使超调量变大,导致产生振荡。加大积分系数Ki有利于减小系统静差,但会加剧超调量,甚至引起振荡;减小积分系数有利于系统的稳定,减少系统超调量,但对消除静差是不利的。
3)微分环节能反映系统偏差的变化趋势,在偏差信号变大之前,引入一个早期修正信号,减小超调,克服振荡,使系统快速趋于稳定,提高响应速度。增大微分系数Kd有利于加快系统响应,但抑制干扰能力减弱;反之,若Kd分配小,系统调节过程的减速就会滞后,超调量增加,降低系统稳定性。可知,对于不同的被控对象只有适当整定PID的三个参数,才能获得满意的控制效果。
1.2 基于模糊推理PID参数自整定原则
根据污水处理鼓风曝气控制过程的特点,结合PID的三个系数Kp、Ki和Kd对控制系统的影响,基于模糊推理PID参数整定原则有如下三条:
1)E很大:说明实际值与参考值误差很大,为了加快系统的响应速度,应取较大的Kp,同时取较小的Kd以避免出现过饱和,Ki取0以避免出现较大的超调。
2)若E ·EC>0:说明实际值与参考值的差距在变大。此时,当误差绝对值较大时,应取较大Kp以改变误差的变化趋势,迅速减小误差绝对值,同时可取较小的Ki和中等的Kd,以提高动态性能和稳态性能;当误差绝对值较小时,可取中等的Kp,同时取较大的Ki和较小的Kd,以提高系统的稳态性能,避免产生振荡。
3)若E ·EC<0:说明实际值与参考值的差距在变小。当误差绝对值较大时取中等的减小误差绝对值,同时取较小的Ki和中等的Kd,以提高动态性能和稳态性能;当误差绝对值较小时,误差变化率绝对值也较小时,可取较小的Kp,同时取较大的和较小的Kd,以提高系统的稳态性能,避免产生振荡。同时,因为系统存在较大的滞后,当误差绝对值较小,误差变化率绝对值较大时,可以认为系统实际值与参考值的差距在变大,此时应迅速降低误差变化率的绝对值,可取中等的Kp,同时可取较小的Ki和较大的Kd,以提高动态性能和稳态性能。
2 基于模糊推理PID参数自整定控制设计
2.1 基于模糊推理PID参数自整定控制构成
基于模糊逻辑PID参数自整定控制包括模糊参数整定部分和PID控制部分,其中模糊参数整定部分按照一定原则对PID参数进行自动校正,PID控制部分实现对系统的控制,首先根据工程师的实际调整经验和技术知识总结成为IF(条件)THEN(结果)形式的模糊规则,并把这些模糊规则及初始的PID参数存入计算机中。根据系统的响应情况,计算出采样时刻的偏差E及偏差的变化率EC,输入控制器,运用模糊推理和模糊规则进行模糊运算,根据不同的误差和误差变化率实时在线整定PID控制器的3个修正参数ΔKp、ΔKi和ΔKd,得到该时刻的Kp、Ki和Kd,实现对PID参数的最佳调整。模糊PID参数自整定控制框图如图1所示。
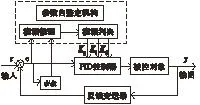
图1 模糊PID参数自整定控制示意图
2.2 模糊自整定PID参数控制实现
利用模糊控制原理确定PID控制器参数的过程主要由模糊化、模糊推理和去模糊化三部分组成。模糊控制系统的设计还要结合工程设计人员的技术知识和实际操作经验,根据系统实际要求,设定各输入输出变量的模糊子集的隶属函数、模糊变量的量化论域和模糊控制规则,建立针对Kp、Ki和Kd三个参数分别调整的模糊规则表。
2.2.1 模糊化及模糊规则库建立
确定模糊变量的量化论域和输入输出变量的模糊子集的隶属函数,将系统误差E和误差变化率EC变化量化论域分为7个模糊子集:
E, EC ={NB, NM, NS, ZO, PS, PM, PB},子集中的元素分别代表负大、负中、负小、零、正小、正中、正大。其论域为E, EC, Kp, Ki, Kd={-3, -2,-1, 0, 1, 2, 3},同时可知各模糊子集的隶属度函数为对称三角形函数,如图2所示。
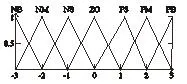
图2 模糊子集隶属度函数
因此可得到各模糊子集的隶属度,根据各模糊子集的隶属度赋值表和各参数模糊控制模型,应用模糊合成推理设计PID参数的调整量ΔKp模糊控制规则如表1所示; 相似可推理出ΔKi和ΔKd。
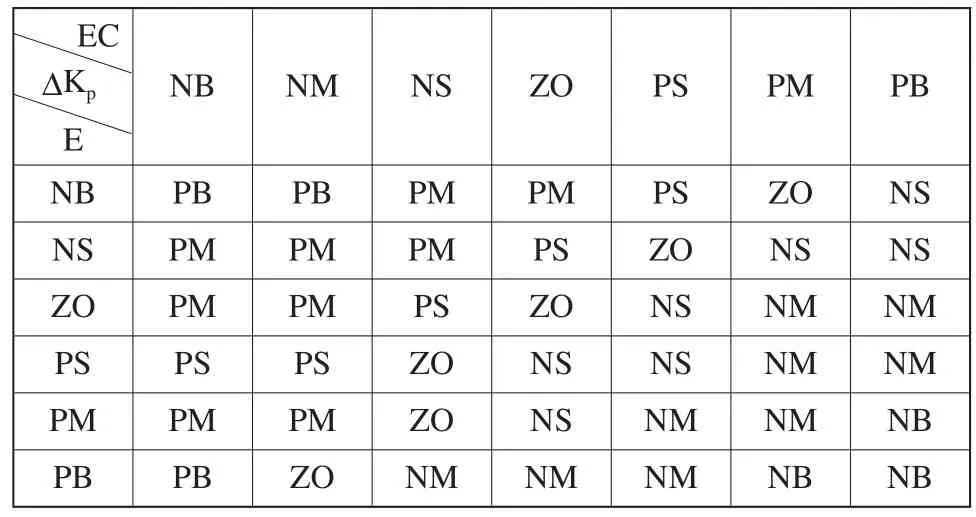
表1 ΔKp调整规则表
模糊规则库中的规则总数为7×7=49条。虽然模糊规则比较多,但因为选用的隶属度函数为对称三角形函数,在一般情况下,偏差e和偏差变化率ec可分别属于两个相邻的可信度不为零的模糊子集中。因此,对于规则if e is E and ec is EC then U,可得模糊规则库中49条规则:
1) if (e is NB) and (ec is NB) then (Kpis NB) (Kiis PS) (Kdis PS)
2) if (e is NB) and (ec is NM) then (Kpis PB) (Kiis NB) (Kdis NS)
3) if (e is NB) and (ec is NS) then (Kpis PM) (Kiis NB) (Kdis NB)
……
48) if (e is PB) and (ec is PM) then (Kpis NB) (Kiis PS) (Kdis PS)
49) if (e is PB) and (ec is PB) then (Kpis NB) (Kiis PB) (Kdis PB)
2.2.2 模糊推理
模糊推理选用Mamdani直接推理法,推理法则为
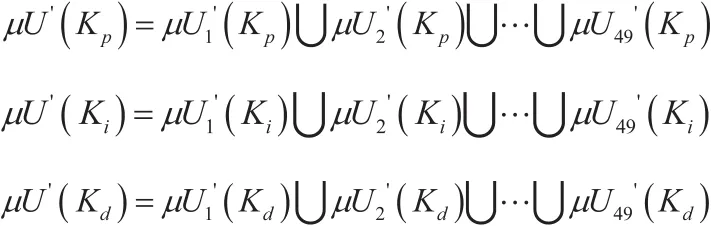
∪表示取大,在一次模糊推理中,隶属度0的规则将不加入到模糊推理中。
2.2.3 去模糊化
这是模糊化的反过程,它把模糊量转变为数值量,也称为模糊判决。去模糊化的方法很多,本文仿真采用加权平均法,其数学表达式为:

上式中:Kpj、Kij、Kdj是各元素在集合中的加权系数,µj(e, ec)是ej×ecj的隶属度,通过上式可计算出ΔKp、ΔKi和ΔKd的数值。实时模糊PID控制参数的调整表达式如下:

式中Kp0、Ki0和Kd0为控制器参数的初始值,可通过分析系统要求得到。
3 鼓风曝气控制设计
3.1 鼓风曝气过程模型建立
由于污水生化处理过程属于复杂的动态工程系统,无法用精确的数学模型来描述,所以在建立鼓风曝气过程动态仿真模型时,忽略生化反应速率变化与微生物代谢作用,假设曝气过程在时间上呈理想的推流变化,反应池中原水溶解氧浓度变化可忽略不计。根据物料平衡算式:质量净变化率=质量输入率-质量输出率-反应消耗速率
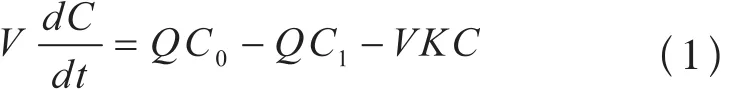
其中:V为反应池容积,C0为鼓入空气的溶解氧浓度,C1为尾气中溶解氧浓度,Q为空气流量,K为反应速率常数,C为反应器中溶解氧浓度,是一个变化量。对式(1)做拉普拉斯变换得:
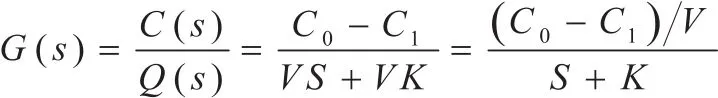
令(C0-C1)/V=R,则有:G(s)=R/(s+k)。这是一个惯性环节,由于DO的检测是非线性,具有滞后特性,将检测滞后用纯滞后τ来表示,得出式G(s)=R/(s+k)e-τs。这是曝气过程的近似模型。
3.2 鼓风曝气控制PID参数自整定
在线运行过程中,首先把溶解氧质量浓度的设定值与测试值相比较,比较结果送入基于模糊推理PID控制器,然后通过控制器和变频器控制鼓风机的转速,从而控制曝气量和曝气池中的溶解氧质量浓度,整个系统是一个闭环反馈控制系统。溶解氧作为模糊控制参数,当DO偏差为正大而偏差变化为正小时,就是曝气池内的DO质量浓度偏大,而且有进一步增大的趋势,应加以调整以节省运行费用。为尽快降低DO质量浓度,必须减小曝气量。由于曝气量随着鼓风机转速的减小而减小,而鼓风机转速与变频器的输出频率有关,所以要尽快地降低频率,控制系统通过对模糊逻辑规则结果的处理、查表和运算,完成对PID参数自整定,通过调节鼓风机的转速,可以改变鼓风机送入池中的风量,从而控制调整曝气池的进气量。控制系统的流程如图3所示。
图3 曝气控制流程图
4 系统仿真
为了观察基于模糊推理PID参数自整定对DO(溶解氧)的控制效果,采用常见的一阶惯性加纯滞后环节传递函数为例,仿真模型为:
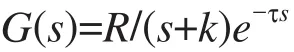
其中:R=2, τ=3s, K=5,在 MATLAB 的命令窗口,输入fuzzy指令,并按上文设计步骤建立一个二输入、三输出的Fuzzy Logic controller,然后用readfis指令将MyFuzzy.fis加载到matlab的工作空间,返回到SIMULINK中,并在Model中双击Fuzzy Logic controller 模块,在Parameters中输入上面所建立的文件Myfuzzy的文件名,将其与PID控制器连在一起,便构成了复合控制器,鼓风曝气的基于模糊推理PID参数自整定控制仿真系统如图4所示,在仿真中加入阶跃信号作为系统的外部扰动,仿真结果对比如图5所示。
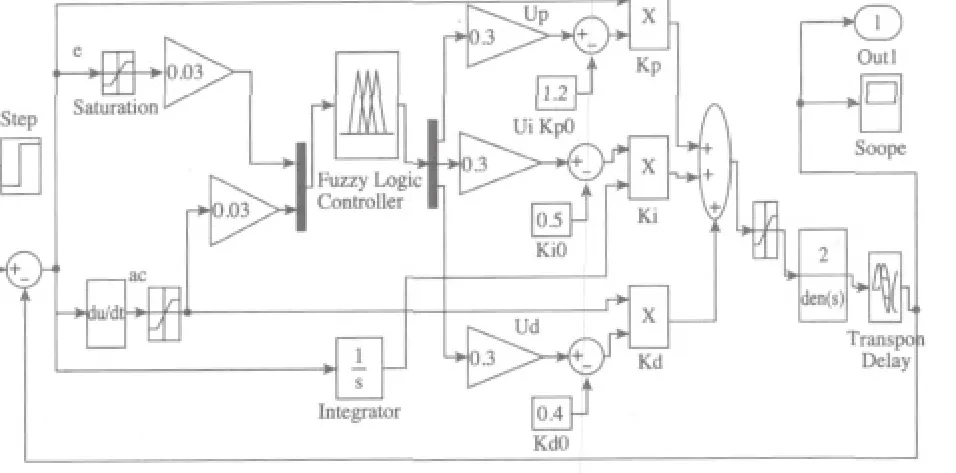
图4 系统仿真框图
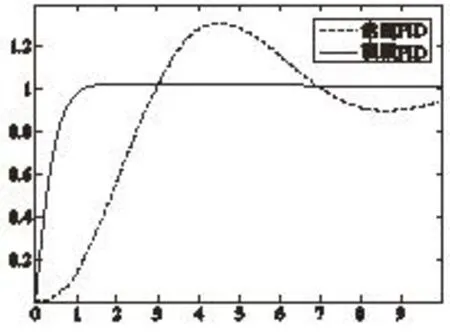
图5 系统阶跃响应曲线
5 结论
通过系统仿真实验可得,基于模糊推理 PID参数自整定控制是在常规 PID算法的基础上, 通过计算当前系统误差 e 和误差变化率 ec, 利用模糊推理,查询模糊矩阵规则库进行参数自调整, 系统的响应速度变快、调节精度提高、稳态性能更好, 而且没有超调和振荡, 具有较强的鲁棒性。这是常规PID控制难以实现的, 基于模糊推理PID参数自整定控制的高精度、快速性、稳定性等显著特点在实际鼓风曝气控制系统中的应用将有重大的意义。
[1] B. M. Mohan Arpita Sinha The simplest fuzzy PID controllers mathematical models and stability analysis [J]Springer-Verlag 2005(10): 961-975.
[2] J. H. Kim S. J. Oh A fuzzy PID controller for nonlinear and uncertain systems [J] Soft Computing 2000(2): 123-129.
[3] 任德齐, 郭兵. 模糊PID参数自整定在炉温控制系统中的应用电气应用[J]. 2008(19): 77-80.
[4] 刘曙关, 魏俊民, 竺志超. 模糊控制技术[M]. 北京: 中国纺织出版社, 2001.
[5] Li Taifu Xiong Jundi Zhang Rui Hardware Implementation of Fuzzy PID Controllers Fuzzy Optimization and Decision Making [J] 2006(2): 113-122.
[6] 杨志, 梅小艳. 污水处理中基于仿人智能的DO参数控制系统[J]. 智能控制技术, 2006(2): 100-104.
[7] 乔志杰; 王维庆. 模糊自适应控制器的设计及其仿真[J]自动化与仪表 2008(01): 26-29.
[8] 徐湘元. 自适应控制理论与应用[M]. 北京: 电子工业出版社, 2007.

