一种高效智能的参数化设计方法
曾文忠
(重庆三峡职业学院, 重庆 404115)
0 引言
随着CAD/CAE/CAM/PDM一体化的设计分析软件不断涌现,比如,UG NX、SolidWorks、Pro/E等。三维模型的设计技术水平不断提高,三维设计软件的功能也不断增强,比如,实体造型、参数化造型、曲面造型等,并且能够进行二次开发,从而能够满足用户在进行模型设计、分析、制造以及数据管理等工作上的要求。
高效智能的参数化设计是进行产品设计的发展趋势,在进行参数化设计的同时,还应该以优化设计为目标,从而能够提高产品的质量。因此,在参数化设计过程中,还应该进行大量的数值计算,从而保证参数的优化设计。MATHCAD是美国PTC公司研发的一款工程计算软件,具有独特的可视化界面,可以在工作表中汇集文本、数学符号和图形,可以和Pro/E之间形成无缝连接,进而有较强的扩展功能。
笔者利用Pro/E三维设计软件的特征建模功能以及MathCAD工程计算软件的编程、计算和显示的优化功能,实现了三维设计软件Pro/E和工程计算软件MathCAD之间的无缝连接,在两个软件之间传输模型参数优化设计的相关数据,完成了蜗轮蜗杆的参数优化设计,并且设计了高效智能的参数优化设计的流程。
1 齿轮参数化建模
1.1 建模思路
蜗轮蜗杆传动具有平稳、振动和噪音小以及结构紧凑等优点,已经成功地应用于化工、冶金、船舶等领域的传动系统中,蜗轮可以传递交错轴的动力和运动。由于其结构复杂,因此建模困难。
蜗轮蜗杆的基本尺寸参数有:压力角α,模数m,蜗杆头数z1,蜗轮头数z2,蜗杆直径系数q,导程角γ,齿顶高系数ha*以及顶隙系数c*。
1.1.1 蜗杆的建模原理
蜗杆的螺旋面和螺纹的形成规律类似,可以通过一个等腰梯形沿呵基米德螺旋线进行旋转切除而得到。
根据蜗杆模型的结构特点,利用Pro/E软件建立蜗杆模型的具体步骤如下:
1)以齿顶圆为轮廓进行拉伸操作获得蜗杆基体。
2)绘制阿基米德螺旋线。
3)建立蜗杆的切除齿廓;
4)以阿基米德线为引导线,以切除齿廓为轮廓,进行扫描切除,从而获得蜗杆的三维模型。蜗杆的实体模型如图1所示。
1.1.2 蜗轮的建模原理
蜗杆和蜗轮在中平面上相当于直齿条和渐开线齿轮啮合。蜗轮齿廓是建模的第一步。利用Pro/E绘制渐开线上的若干点,绘制出样条曲线作为渐开线。

图1 蜗杆的实体模型
利用Pro/E建立蜗轮的三维模型的步骤如下:
1)通过拉伸操作获得蜗轮基体;
2)绘制渐开线、喉圆和齿根圆形成齿廓;
3)以齿廓为轮廓,以阿基米德线为引导线,进行扫描切除,获得单个齿槽;
4)将“扫描-特征”进行阵列,可以获得蜗轮造型;
5)进行细节操作,比如,倒角、圆角等,获得蜗轮模型。蜗轮的实体模型如图2所示。

图2 蜗轮的实体模型
1.2 参数优化设计思路
蜗轮蜗杆设计需要较高的精确度,并且具有较好的接触性能、润滑性能以及抗磨损能力和抗胶合能力。但是在啮合精度、蜗轮蜗杆强度和转速上都具有较高的要求。
笔者在考虑蜗轮蜗杆性能特点和工作环境的前提下,确定蜗轮与蜗杆中心距以及蜗杆的直径为最小作为优化设计的目标函数,利用MathCAD中Minimize函数可以获得满足优化目标函数的蜗轮蜗杆结构尺寸参数,从而能够获得性能最佳的蜗轮蜗杆结构。
2 蜗轮蜗杆参数优化的数学模型
2.1 目标函数
蜗轮蜗杆所构成减速器的重量主要由蜗轮蜗杆的结构和尺寸来决定,蜗轮蜗杆的中心距A和蜗杆的直径d是决定减速器体积的关键尺寸,当减少蜗轮蜗杆的直径和中心距时,可以使减速器的重量得到减少,因此蜗轮蜗杆参数优化设计的目标函数可以表示为如下的式子:
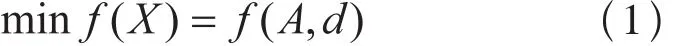
2.2 蜗轮蜗杆参数优化设计的设计变量
为了能够提高蜗轮蜗杆的工作效率,提高其工艺性,可以利用健联结和轴孔之间形成过盈配合来实现传动,同时将蜗杆和轴制成一个蜗杆轴。因此,可以选择以下参数优化设计的设计变量:压力角α,模数m,蜗杆头数z1,蜗轮头数z2,蜗杆直径系数q,导程角γ,齿顶高系数ha*以及顶隙系数c*,设计变量如下所示:

2.3 蜗轮蜗杆参数优化设计的约束
2.3.1 蜗轮蜗杆传动比的约束条件
蜗轮蜗杆的传动比应该是整数,可以有一定的误差,相应的约束条件可以表示如下的形式:

2.3.2 蜗轮蜗杆的齿数的约束条件
为了确保在加工蜗轮和蜗杆的过程中不产生根切,蜗轮蜗杆的齿数应该满足如下的条件:

2.3.3 蜗轮蜗杆的模数约束条件
为了能够提高蜗轮蜗杆加工工艺性,保证加工质量,可以根据实际经验建立蜗轮蜗杆的模型数条件:

式中,m1和m2是设计者给出的模数范围。
2.3.4 蜗杆直径系数的约束条件
当模数不变时,蜗杆直径系数越大,蜗杆直径就越大,反之,蜗杆直径则减少,进而改变蜗杆的刚度和强度。根据设计经验,蜗杆直径系数的约束条件可以表示为如下的形式:

式中,q1和q2是设计者给出的模数范围。
2.3.5 蜗轮的接触强度约束条件
蜗轮蜗杆传动过程中,蜗轮与蜗杆之间的接触疲劳强度约束条件可以表示为如下的形式:

式中,zE表示材料的弹性系数;KA表示工作状态系数;KV表示动载系数,主要由蜗轮旋转的圆周速度来决定;Kβ为齿间载荷分布系数,主要通过载荷的使用情况来决定;[σH]表示蜗轮制造材料的许用接触应力;T2表示蜗轮在扭转时所承受的扭矩。
2.3.6 蜗轮齿根弯曲疲劳强度约束条件
蜗轮齿根弯曲疲劳强度的约束条件可以表示为如下的形式:
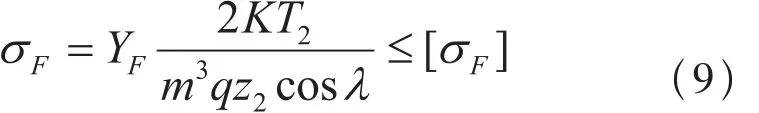
式中,YF表示蜗轮的齿形系数,该系数可以依据蜗轮的齿数来选取; σF表示蜗轮蜗杆齿根许用弯曲应力;λ表示蜗轮的导程角,λ和蜗杆的直径系数以及蜗杆的齿数相关,它们之间的关系表达式如下所示:

2.4 蜗轮蜗杆参数优化设计流程
蜗轮蜗杆的参数优化设计主要包括两个重要组成部分,一个是参数优化计算模块,可以利用MathCAD工程计算软件来完成;另外一个是参数化绘图模块,可以利用三维设计软件Pro/E来实现,MathCAD软件具有蜗轮蜗杆尺寸参数数据的显示和查询功能,利用MathCAD软件进行对蜗轮蜗杆尺寸参数进行优化设计,最终将优化结果输出,并且利用Pro/E软件绘制三维模型。蜗轮蜗杆参数优化设计的流程图如图3所示。

图3 蜗轮蜗杆参数优化设计流程图
3 蜗轮蜗杆的参数优化分析
在蜗轮蜗杆的参数优化设计过程中综合了MathCAD软件强大的计算功能以及Pro/E软件强大的三维绘图功能,可以实现对蜗轮蜗杆智能化的参数优化设计。Pro/E和MathCAD联合工作流程如图4所示。
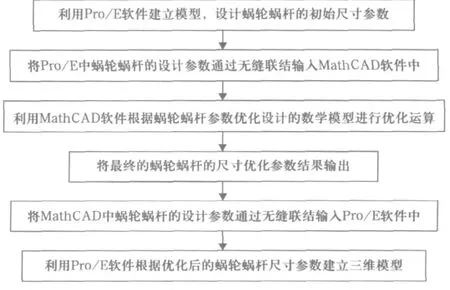
图4 Pro/E和MathCAD联合工作流程图
以一个传动比为i=20的蜗轮蜗杆减速器为例,对其进行参数优化设计,主要设计参数如下所示:蜗杆轴的输入功率为8kW,蜗杆轴转速为1980r/min,该减速器每年工作350天,每天的工作时间为7个小时。
根据设计经验m1=2和m2=12,q1=6和q2=20,1≤z1≤4,26≤z2≤75,蜗轮和蜗杆制造材料为ZCuSn10Pb1和45号钢,许用接触应力为σH=163MPa,蜗轮蜗杆齿根许用弯曲应力σF=32.9MPa。
将初始参数输入MathCAD进行优化设计,利用Minimize函数进行运算,具体操作步骤如下:
单击主菜单上“分析”菜单→“外部分析”菜单→“MathCAD分析”菜单。将弹出一个对话框,在对话框中选择“新文件”按钮单击,可以将MathCAD软件打开,选择MathCAD软件菜单项上“文件”菜单→“新建”,一个新的MathCAD文档将被打开,在文档中建立上述蜗轮蜗杆的参数优化设计数学模型,利用复合形法进行优化计算,最终可以求解出蜗轮蜗杆的尺寸参数的最优值。
为了能够使在MathCAD软件和Pro/E软件之间传输的数据传输的过程中更加清晰,为设计变量分别定义一个标签,具体的操作方法如下:
选中某个设计变量的定义式,点右键,选择“属性”选项,会弹出“显示”选项卡,在其中选择“标签”并输入“proe2mc”或“mc2proe”,设计变量α, m, z1, z2, q, γ, ha*, c需要添加标签:ma,mm, mz1, mz2, mq, mγ, mha, mc。完成操作后,将文件保存为“wear. xmcd”。
接着,点击“加载文件”选项,选择刚刚生成的“wear.xmcd”文件。点击“添加参数”,会弹出一个对话框,在对话框中“参数选取”选项中Pro/E的设定参数,点击“确定”,然后在“输入选取”对话框中选取MathCAD中设定参数。
然后,将MathCAD中的变量输入至Pro/E软件。点击“输出”,在弹出的“输出选取”对话框中选则需要输出到的Pro/E中得参数,压力角α,模数m,蜗杆头数z1,蜗轮头数z2,蜗杆直径系数q,导程角γ,齿顶高系数ha*以及顶隙系数c*。在对话框中点击“计算”→“添加特征”,将分析命名,最后,点击“关闭”按钮,完成了分析特征的创建。
接下来,把MathCAD软件中获得的蜗轮蜗杆优化参数输入Pro/E软件中,从而使蜗轮蜗杆的三维模型得到更新,需要在Pro/E中添加相应的关系式,比如:
A:2=MC_MA:FID_ANALYSIS1
M:2=MC_MM:FID_ANALYSIS1
Z:2=MC_MZ1:FID_ANALYSIS1
Z:4=MC_MZ2:FID_ANALYSIS1
Q:4=MC_MQ:FID_ANALYSIS1

图5 优化后的蜗轮蜗杆三维图
Y:6=MC_MY:FID_ANALYSIS1
H:6=MC_MHA:FID_ANALYSIS1
C:6=MC_MC:FID_ANALYSIS1
最后,将Pro/E中蜗轮蜗杆尺寸参数进行修改,重新生成蜗轮蜗杆的三维模型。MathCAD软件和PRO/E软件之间能够进行无缝的数据联结,并且实现蜗轮蜗杆三维模型的同步更新。参数优化设计后的蜗轮蜗杆如图5所示。
4 结束语
利用Pro/E软件和MathCAD软件对蜗轮蜗杆进行参数优化设计,不仅能够提高三维建模的效率,同时也能够对蜗轮蜗杆的结构尺寸进行优化设计,从而能够提高蜗轮蜗杆传动的性能,提高以蜗轮蜗杆传动为传动系统的机械设备的整机性能,同时也可以提高设计效率,节约设计成本,从而为机械设备的参数优化设计提供一种高效智能的优化设计方法。
[1] 阮锦, 刘强, 阮锋. 蜗轮蜗杆的三维参数化设计及运动仿真分析[J]. 机械设计与制造, 2006, 27(7): 74-77.
[2] 郭帅, 师帅兵, 韩雪. 基于SolidWorks 的蜗轮蜗杆参数化设计[J]. 农机化研究, 2011, (3): 66-70.
[3] 李立新, 江玉刚, 曹谊勃. 基于精确齿面建模的ZA 蜗杆蜗轮有限元接触分析[J]. 工程设计学报, 2011, 18(1): 38-44.
[4] 李立新, 曹谊勃. 基于双三次B样条曲面的ZA蜗轮实体建模方法[J]. 工程设计学报. 2009, 16(4): 286-291.

