薄片类零件平面磨削区表面温度场的计算研究
朱传敏 ,宋崇金 ,郭知令,于 立,冯 凯
(同济大学 机械工程学院,上海 201804)
0 引言
磨削加工是现代机械制造业中进行精密加工和超精密加工的重要工艺技术。在磨削加工中,所消耗的能量大部分转化为热能传入被磨工件,传入工件的热量主要集中在很薄的表面层里,形成局部高温,这种现象对工件表面质量和工件的使用性能影响很大。国内外大量专家学者对磨削加工中的热效应问题进行了研究。1942年,J. C.Jaeger[1]首先提出了移动热源理论,Outwater和Shaw[2]基于剪切面移动热源理论建立了热量传递给工件的热源模型, 1996年Rowe[3]在前人研究的基础上综合考虑了工件的热特性、砂轮的锋利程度、砂轮和工件的速度、切深以及接触长度对温度场的影响。我国学者贝季瑶教授[4]早在上世纪60年代就提出了热源强度在沿接触弧长上为三角形分布的假设,高航教授[5]在研究断续磨削时分别建立了卧轴周边断续磨削和立轴端面断续磨削的热源模型。磨削过程的热效应一直是国内外学者研究的热点。
随着航天和汽车技术的发展,出现了越来越多的薄片类零件,如航天仓中的各种密封圈和垫片。这类零件的磨削质量要求很高,磨削过程中的热效应容易使零件变形和烧伤,影响了磨削质量和使用性能。精密磨削过程中的热效应问题,已逐渐成为制约薄片类零件磨削加工工艺发展的瓶颈,因此对薄片类零件平面磨削过程中的热效应问题进行研究具有理论意义和实际应用价值。
1 薄片零件平面磨削表面温度场的计算理论研究
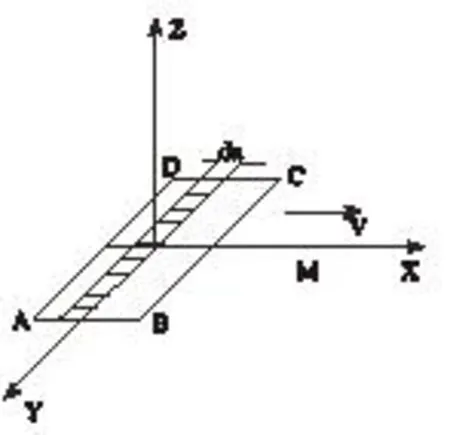
图1 薄片零件运动面热源温度场坐标
如图1所示面热源ABCD沿X方向以速度V在无限大的薄片零件内运动。
按照两维传热模型计算,则薄片平面内X轴上任意一点的温升为[6]

根据式(1)可以计算薄片零件表面内沿X轴方向上任意点的温度。
按照一维传热模型计算,将面热源看成只沿Z方向传入零件内。则当面热源运动到M点后,在面热源区域下Z方向上任意点的温升为[6]。
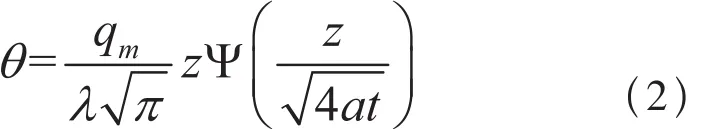
薄片零件磨削区表面的温升为

由于移动面热源在任一瞬间同时存在两维传热和一维传热,如图2所示。设有εqm的热量按一维传热,忽略其他热量损失,根据能量守恒则有(1-ε) qm的热量按照两维传热。
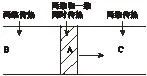
图2 薄片零件平面磨削热传导类型分布
则薄片零件表面磨削区任一点的温升可表示为:

令ε=f (v),且0<ε<1,当工件移动速度v→∞时,ε→0;公式(4)等效于公式(1)二维传热,当工件移动速度v→0时,ε→1公式(4)等效于公式(2)按一维传热。对于磨削区中确定一点,在其他磨削参数不变的情况下,某一确定时刻
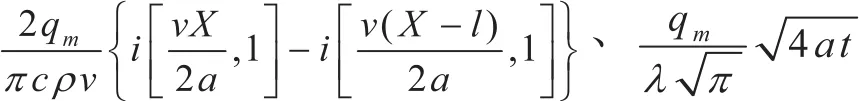
均为定值,可以设为K1、K2,则式(4)可以化为:
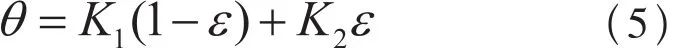
2 平面磨削区表面温度场计算与仿真
2.1 平面磨削区表面温度场的理论计算
取磨削总发热功率qm=782.125cal/cm2s(假设热量全部传入工件),密度ρ=4.43g/cm3,热扩散率 a= 0.05079cm2,比热容 c= 0.12cal/g ·℃,热源移动速度v=23.33cm/s,工件导热率λ=0.027cal·s·℃,磨削区接触长度取 0.156cm。
对于磨削区温度场的计算既可采用二维传热模型计算也可以按一维传热模型计算[6]。
按照二维传热模型计算公式(1)
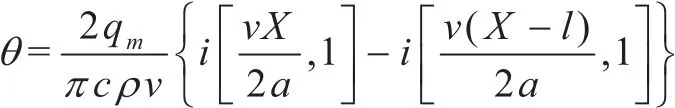
查表[6]可以计算出磨削表面最高温度为在X=0处θmax1=568.8℃
按照一维传热模型计算公式(3)

按照二维和一维同时传热模型计算公式(4)
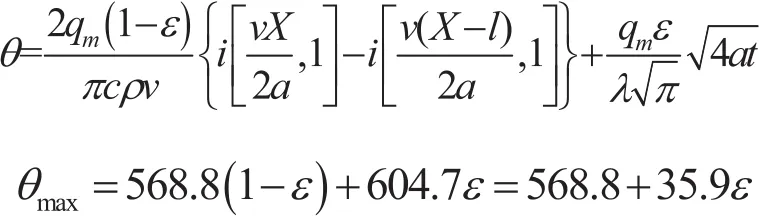
其中0<ε<1。
显然: θmax1<θmax<θmax2。
2.2 有限元仿真分析
有限元仿真一般分三大步骤:1)建立有限元模型;2)加载和求解;3)后处理和结果查看。如图3所示。
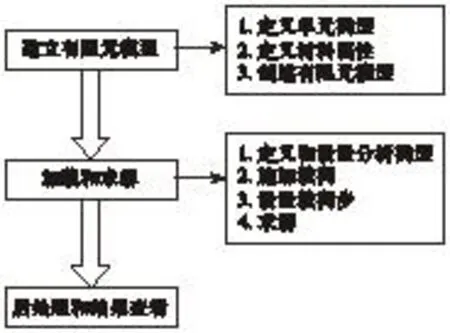
图3 有限元仿真分析流程图
定义有限元模型为长、宽、高分别是120mm、30mm、1mm的薄片零件,定义材料属性,密度ρ=4.43g/cm3,热扩散率a=0.05079cm2,比热容 c = 0.12cal/g ·℃。
在有限元分析中,附加合适的边界条件和初始条件关系着有限元仿真结果的好坏,在磨削过程中由于空气导热系数很小,因此可以不考虑空气的对流传热,将其视为绝热,初始条件设为室温20℃。
对于网格划分如果单元过大计算结果会产生很大的误差,如果网格划分过小,会影响计算机处理时间,这里采用高级建模技术对网格细化[7],这样计算结果就较为准确,网格划分结果如图4所示。

图4 有限元网格划分结果
由于有限元本身不能加载移动热源,通常解决此类问题的方法是将过程离散化,在极短时间内在某一磨削区加载一个固定热流,在下一极短的时间内再将热源加载到另一位置,并将上一次所得结果作为初始条件。经过多次迭代和加载就能得到磨削区温度分布。如图5所示。
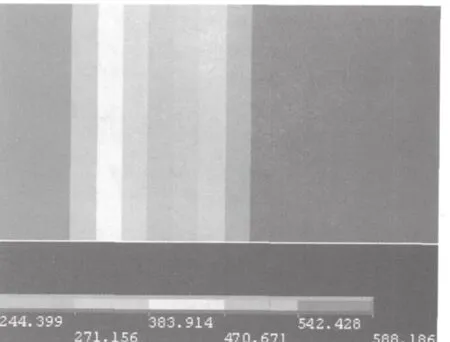
图5 v=23.33cm/s时薄片零件表面某时刻的温度场
从有限元仿真结果可以发现在某时刻磨削区的温度最高可达588℃,令θmax=588即:θmax=568.8+35.9ε=588,可以解得:ε≈0.557,再将ε≈0.557代入公式(5)即可得到薄片零件平面磨削区表面温度场在v=23.33cm/s 条件下的计算公式:
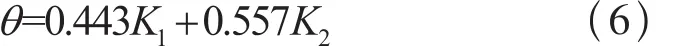
其中:
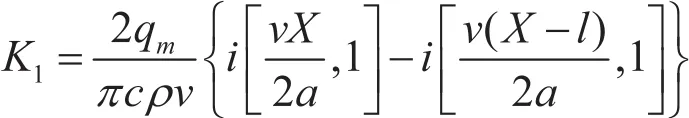
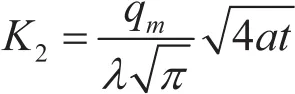
查表[7]分别计算磨削区下列各组点的温度如图6所示。
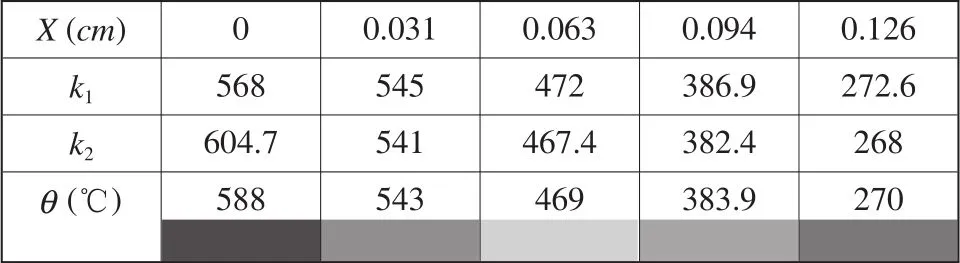
图6 磨削区部分点的温度值
其中k1是按二维传热模型计算的温度,k2是按一维传热模型计算的温度。
3 结论
本文通过对薄片零件平面磨削区表面温度场的两种传热模型(二维传热和一维传热)进行分析,提出了一种二维和一维同时传热模型。通过理论计算和有限元仿真对比分析。验证了这种二维和一维同时传热模型计算结果比一维或二维传热模型更加接近仿真结果。
通过实验测量薄片零件磨削区表面的最高温度,计算出ε,在其它磨削参数不变的情况下,找出ε和工件移动速度v之间的函数关系,便可根据工件移动速度v估算出磨削零件表面的最高温度。为平面磨削加工选择合适的工件移动速度v提供了依据,具有理论和现实意义。
[1] J. C. Jeager, Moving Source of Heat and the Temperature at Sliding Contacts, Proc. Roy. Soc of New South Wales,1942, 76: 203-224.
[2] J. 0. Outwater and M. C. Shaw etc, Surface Temperatures in Grinding Transaction of the ASME, 1952, l: 213-221.
[3] Rowe, W. B. , Morgan, M. N. , Black, S. C. E. , Mils, B. , A simplified approach to thermal damage in grinding. Annals of the CIRP, 1996, 45/1: 299-302.
[4] 贝季瑶. 磨削温度的分析与研究[J]. 上海交通大学学报,1964, 9(3).
[5] 高航. 高效立轴平面强力磨削技术与机理的研究[D]. 沈阳: 东北大学, 1992.
[6] 任敬心, 华定安. 磨削原理[M]. 电子工业出版社.
[7] 邓凡平. ANSYS 10.0有限元分析自学手册[M]. 人民邮电出版社.

