新型变螺旋角正弦斜齿轮的啮合特性分析
黄道业,孟凡净
(安徽国防科技职业学院 机械工程系,六安 237000)
0 引言
正弦变螺旋角斜齿轮传动,是一种两轴三自由度的应用正弦函数曲线构造齿轮基本齿廓的直、斜齿之间的共轭传动,该齿轮传动型式比较新颖,一方面该齿轮传动探索性的应用了一种新型的齿廓型式-正弦函数曲线,另一方面它打破了常规的齿轮传动规律的传动方式,相共轭的一对齿轮的螺旋角不等,其主动齿轮为直齿抡,从动轮为变螺旋角斜齿轮(即螺旋角大小和方向均按一定的规律发生周期性的变化)。直、斜传动技术是国外抛光磨头的关键技术,并且该技术长期以来受到国外封锁和保密。我国现阶段对于该技术完全处于测绘和仿制阶段,产品质量不高、抛光效果较差。因此对于正弦直、斜齿传动啮合原理进行研究,通过该研究总结出设计和制造经验就显得尤为重要。本文正是基于以上原因对该新型的齿轮传动的齿面方程和实体模型做了以下研究[1~3]。
1 坐标系的建立[4]
根据齿轮的坐标建立方法,正弦齿廓直齿轮和斜齿轮啮合过程中采用如下四个坐标系(如图1所示),初始位置的两个固定坐标系:SZOOZOxZOyZOzZO和SXO-OXOxXOyXOzXO;与正弦齿廓直齿轮和斜齿轮固连的两个动坐标系SZ-OZxZyZzZ和SX-OXxXyXzX。初始时,zZO轴与zXO平行,yZO轴与yXO平行,xZO与xXO轴重合,OZOOXO=a;坐标系SZ-OZxZyZzZ与SX-OXxXyXzX分别与坐标系SZO-OZOxZOyZOzZO与SXO-OXOxXOyXOzXO重合。啮合时,正弦直齿轮仅仅以角速度1绕zZO轴转动,OZOOZ=0;正弦斜齿轮一方面绕zZ轴以角速度X转动,同时以角速度XO绕xXO轴转动,OXOOX=0。
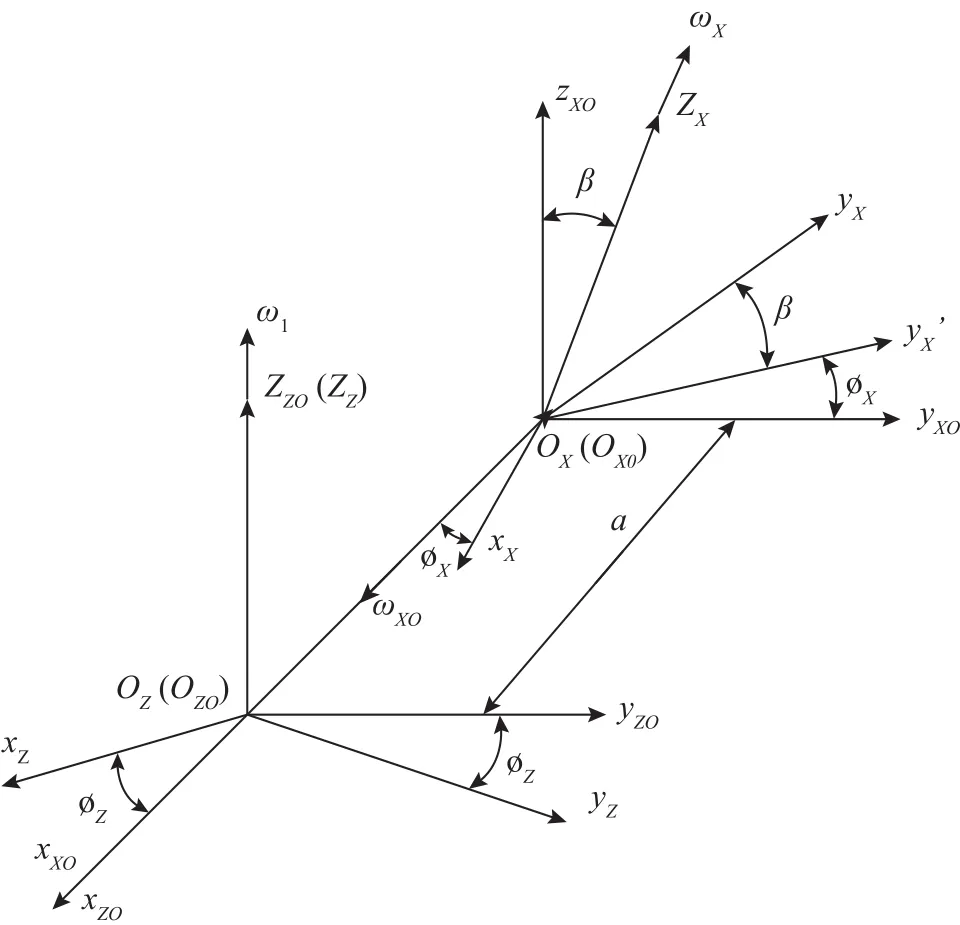
图1 坐标变换关系
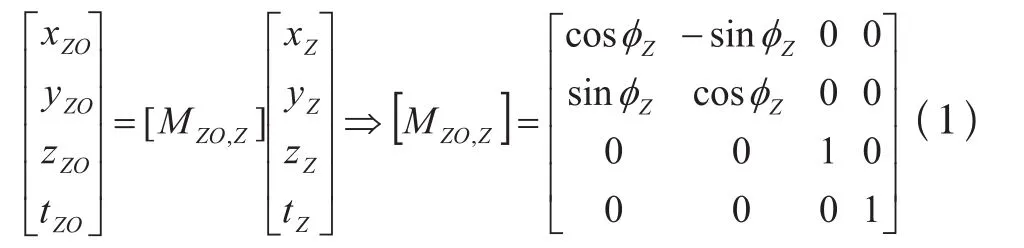

由(1)、(3)、(4)式可以得到由坐标系SZ0-OZ0xZ0yZ0zZ0到SX-OXxXyXzX的变换矩阵为[MZO,X]为:

2 基本正弦齿廓的建立
如图3所示,以正弦函数曲线的坐标系零点作为该齿轮的分度圆;以正弦函数曲线的幅值H作为该齿轮的齿顶高和齿根高;以正弦函数曲线的一个周期作为该齿轮的齿距来构造该新型的齿轮齿廓方程。为了能够建立好该齿轮的齿廓方程,特建立了图2所示的旋转坐标系S-OXY和图3所示的直线坐标系S1-O1X1Y1,齿廓构造函数为Y1=Hsin (BX1),其中B 为正弦函数的周期系数。
则正弦齿轮的基本齿廓方程用极坐标可表示为:
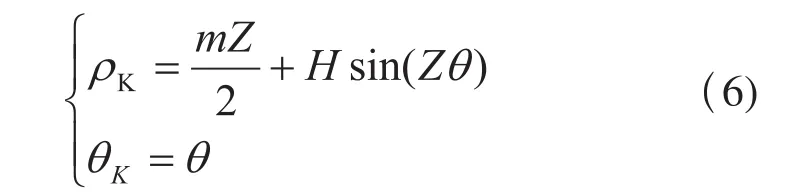
极坐标方程转化为直角坐标方程为:
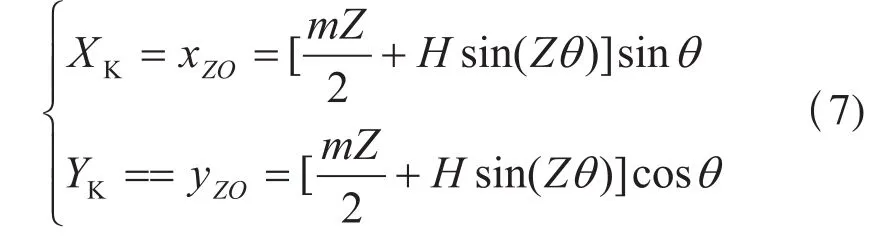
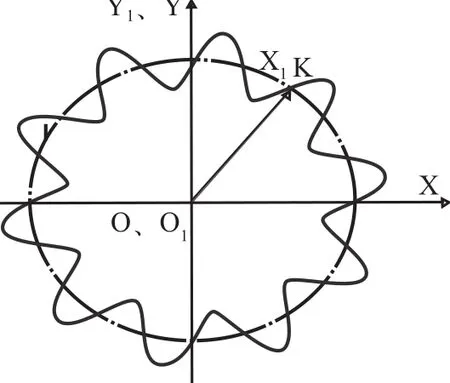
图2 旋转坐标系S-OXY

图3 直线坐标系S1-O1X1Y1
3 变螺旋角正弦斜齿轮的齿面方程[5]
3.1 法线矢量
正弦直齿的基本齿面由坐标系SZO-OZOxZOyZOzZO变换到坐标系SZ-OZxZyZzZ后的齿面方程为:
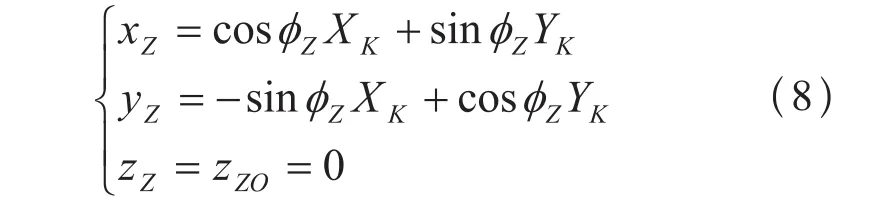
对于正弦直齿齿面上的任意点P (xZ, yZ, zZ),设其在动坐标系SZ-OZxZyZzZ中的矢径rZ为:
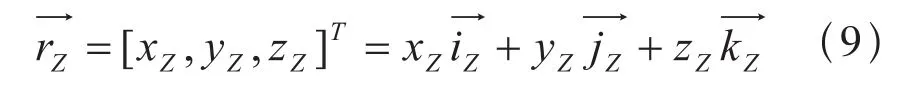
根据(9)式分别对 和H求导,化简得法向量为:

3.2 接触处的相对速度
如图4所示,设空间有一点M在坐标系SZO-OZOxZOyZOzZO中 的 坐 标 为(xZO, yZO, zZO),令OXOOZO=aiZO,则:

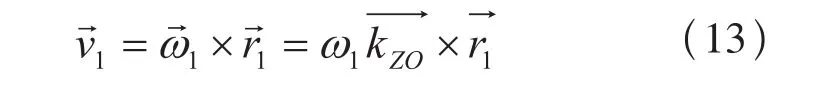
其中,1为直齿轮绕zZO旋转的角速度模量。
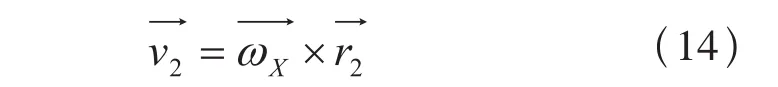
因为斜齿轮绕zX轴转动的角速度:且绕xXO转动的角速度:由(4)可得斜齿轮在坐标系SZO-OZOxZOyZOzZO中的角速度为:

图4 相对速度坐标图


式中:
2——斜齿轮绕zX轴旋转的角速度模量;XO——斜齿轮绕xXO旋转的角速度模量。两齿轮在接触处的相对速度为:

其中, 为大小和方向均按一定的规律发生周期性的变化的螺旋角的函数:
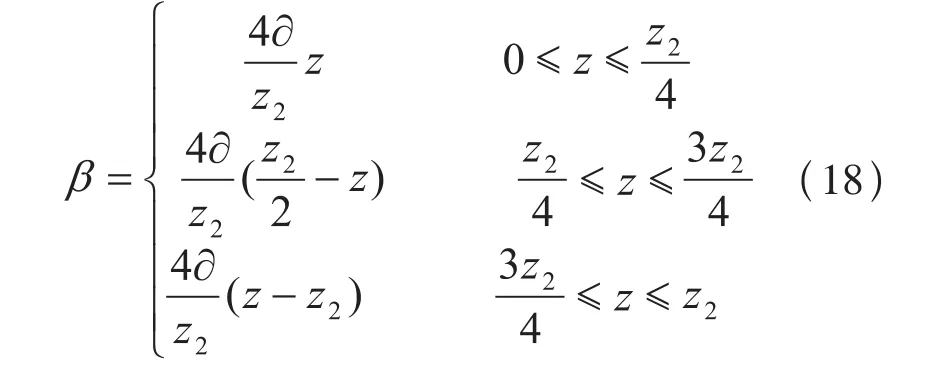
式中:
z2——变螺旋角正弦斜齿轮的齿数;
——变螺旋角正弦斜齿轮螺旋角的变化幅度,如图5所示。
3.3 变螺旋角正弦斜齿轮传动的齿面方程
由齿轮啮合原理可知,两齿轮齿面的啮合条件是:


图5 螺旋角周期性变化图
把(13)和(17)式代入后得到两齿轮啮合的啮合方程为:
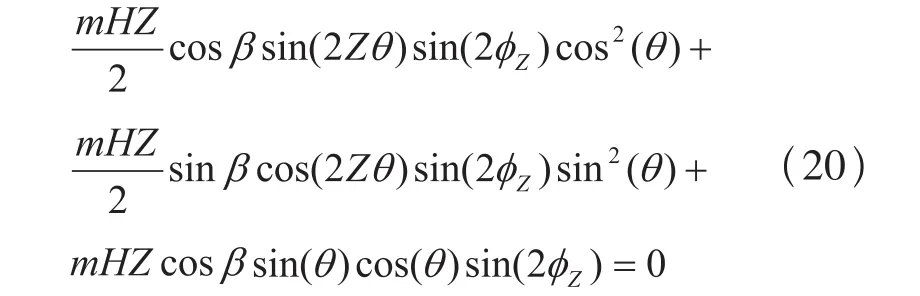
联立(8)和(20)可以得到弧齿直齿轮和变螺旋角斜齿轮传动在SZ-OZxZyZzZ中的齿面方程为:

由(3)、(4)式可以得到弧齿直齿轮和变螺旋角斜齿轮传动在SX-OXxXyXzX中的齿面方程为:
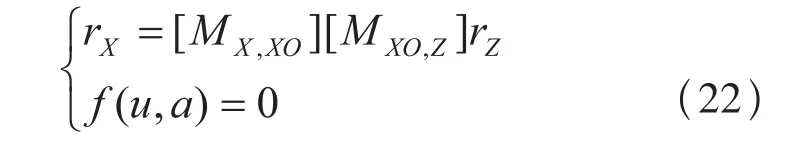
4 啮合轨迹的计算机仿真[6~8]
4.1 参数选择和计算
根据新型正弦齿轮的参数特点对一对相啮合的正弦直齿轮和变螺旋角的主要啮合参数做了如下的选择和计算。
基本参数:直齿轮的齿数Z1=20,模数m=5,变螺旋角斜齿数Z2=60,=5° 15°。
4.2 仿真分析
由于正弦直斜齿传动的瞬时接触线只是一种理想的情况,而在实际过程中为点接触,对理想情况分析没有实际意义,因此本文在分析过程中只对点接触的情况进行分析。在仿真过程中,为了使仿真的结果易于分析和处理,特对仿真的步骤做了如下的规定:
1)固定 =15°,取H分别等于5mm和10mm时的仿真结果,如图(6)所示。
2)固定H=10mm,取 分别等于5°和10°时的仿真结果,如图7所示。

图6 仿真图H

图7 仿真图
从图6可以看出,接触轨迹随着H值的增大移向齿高的正向,齿宽的正向。从图7可以看出,接触轨迹随着 角度的增大将移向齿高的负向,齿宽的负向。
5 结论
1)基于《齿轮啮合原理》和《微分几何》的知识推导了变螺旋角正弦斜齿轮的齿面方程。
2)应用仿真软件MATLAB6.0对变螺旋角正弦直斜齿传动的啮合轨迹仿真分析。分析结果表明:接触轨迹随着H值的增大移向齿高的正向,齿宽的正向。接触轨迹随着 角度的增大将移向齿高的负向,齿宽的负向。
[1] N.E.Anderson. Design of Spur Gears For Improved Efficiency[S]. ASME Mech, 1984, 104.
[2] D.N.Timmerman. How To Select Process Equipment Gear Drives[S]. E/MJ-June, 1971, 7.
[3] Chotaro. Naruse etc. Influence of Tooth Profiles Upon Limiting Load For Scoring And Frictional Loss of Spur Gear[S]. 1984, 27(25).
[4] 吴序堂. 齿轮啮合原理[M]. 机械工业出版社, 1982 .
[5] 唐余勇. 微分几何讲义[M]. 高等教育出版社, 1985.
[6] 王三民. 航空发动机主传动弧齿锥齿轮的接触特性研究[J]. 航空动力学报, 1994(1).
[7] 刘志峰, 杨文通, 王国权, 等. 摆线锥齿轮边缘接触分析与仿真研究[J]. 机床与液压, 2004(12).
[8] 李丽, 王振. MATLAB工程计算及应用[M]. 人民邮电出版社, 2001.

