基于子结构技术的金属软管静力学性能分析

韩淑洁

（青岛远洋船员职业学院，青岛 266071）

0 引言

金属软管在工作中不仅能吸收由压力、轴向力、横向力、弯曲以及温差等原因所引起的位移，而且可以吸收管路系统的振动，起到减振和降噪的作用，在管路设备和压力容器中得到广泛的应用。船舶柴油机的排气管，发动机的废气回路管、机油回路管、排气歧管补偿器以及燃油冷却器中广泛应用金属软管。研究金属软管的静力学问题，即金属软管在轴向拉伸、轴向压缩、横向错动、弯曲和多载荷联合工况下的静力学特性，对金属软管的推广使用和标准化有着重要意义。

金属软管主要由波纹管、网套和接头三大部分构成[1]，如图1所示。波纹管是具有横向波纹的圆柱形薄壁壳体，是金属软管的主体，用来吸收由于热胀冷缩等原因引起的管道和（或）设备尺寸变化[2]，为了保护波纹管免受机械损伤，在实际应用中一般都在波纹管外层铠装金属丝网套，并用接头连接。

图1 金属软管模型图

由于金属软管结构复杂，对其进行传统的理论计算存在相当大的困难，目前，国内外对金属软管的研究主要采用有限元法，且主要集中在其主体波纹管部分，对于金属软管的研究则很少。由于钢丝网套在波纹管上的覆盖率较大，锭数较多，每锭钢丝的根数也较多，采用有限元法计算时，节点数目较多，对计算机设备资源要求很高，计算时间非常长，目前的研究大都采用简化方法，用一根钢丝代替一锭钢丝来实现对金属软管性能的分析。

子结构技术有降阶凝聚、分阶段求解的特点，非常适合对大型复杂结构进行有限元分析，而金属软管的网套属于非线性问题，带有大量的重复结构，而且工作过程中还存在大转动，所以如果将网套中的一根钢丝运用子结构技术凝聚成一个超单元，采用子结构法建立金属软管的有限元模型，这样可以大大减少运算过程中的节点数量，节省计算机资源，减少运算时间。本文采用子结构技术建立了有限元模型，对金属软管在轴向拉伸、轴向压缩、横向错动、弯曲和多种载荷工况下的静力学特性进行了分析。将分析结果与试验进行了对比，证明了子结构技术建立的金属软管模型的可靠性。

1 子结构技术的理论分析[3]

子结构的刚度阵及载荷矢量的生成方法与常规有限元分析是不同的，考虑到子结构的有限元模型的平衡方程为：

子结构的求解过程包括将上述等式分解，获得局部求解，然后局部求解又组集到整个求解中去，子结构的结点位移可分成两组，第一组是同其他子结构或单元共用，有位移协调关系，属于边界结点位移，用下标B表示。第二组是与其他子结构或单元没有位移陇调关系，用下标I表示，因此式（1）可分解为

将上式展开可得：

求出内部结点位移为：

上述等式右边第一项一种内部结点的局部求解，在内部结点上的其余求解是由于运动边界结点生成的局部求解，为等式右边的第一项，展开后为：

即

上述等式反复赋给不同的子结构，整个系统的刚度矩阵为：

式中nel为主结构的单元数量；nsel为联接主结构的子结构的数量。

由此可知，一旦计算出边界结点或子结构结点位移，则所有子结构的位移和应力都可以由式（1）解出。由于边界刚度矩阵[KBB]*的阶数远小于子结构刚度矩阵的阶数，使得最后组集各个子结构所得到的结构刚度矩阵的阶数大大降低，故应用子结构法可以利用有限的计算机资源解算大型结构问题。

2 利用子结构建立金属软管的有限元模型

在ANSYS中利用子结构建立有限元模型分为三个部分：生成部分、使用部分和扩展部分[4]。

2.1 生成部分

生成部分是将一系列普通的有限元单元凝聚为一个超单元。凝聚是通过定义一组主自由度来实现的，主自由度用于定义超单元与模型中其它单元之间的边界，提取模型的动力学特性。采用beam189单元描述钢丝，对其单元实参、材料特性进行定义，施加边界条件，生成超单元矩阵，按照其螺旋线方程，取与波纹管波峰接触处的各点为主自由度，如图2所示，将一根钢丝凝聚成一个超单元。图2中的各点即为主自由度，为了便于观察，图中仅显示了节点和节点编号。

图2 子结构上的主自由度节点

2.2 使用部分

使用部分是将生成部分的超单元与模型整体相连进行分析，将波纹管作为非超单元部分。建立非超单元模型，如图3所示。

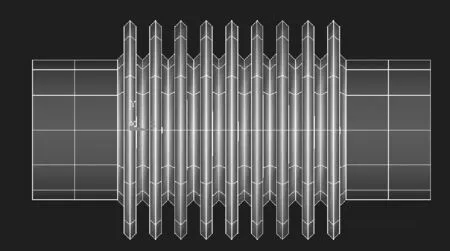
图3 波纹管的有限元模型

利用约束方程建立超单元与非超单元之间的连接。当网套钢丝上的主自由度节点恰好经过波纹管波峰上的节点时，按照约束方程（11）建立钢丝节点和波纹管波峰节点之间的连接，从而保证变形后波纹管波峰与网套之间的接触关系

式中UX1为波纹管上节点的径向变形，UX2为网套钢丝上节点的径向变形。

由于计算量的限制波纹管波峰上的节点在保证计算精度的情况下通常不需要太多，而通过波纹管波峰的网套钢丝的根数通常较多，所以波纹管波峰上的节点不可能与网套钢丝上经过波纹管波峰的节点一一对应。当网套的节点处于波纹管波峰上两相邻节点之间时，波纹管波峰上没有节点与之对应，这时，根据直线拟合理论（如图4所示）推导出约束方程（12），按照约束方程（12）建立波纹管波峰节点与网套节点之间的关系。

图4 波纹管与网套之间的拟合原理图

如图4所示，N1、N2为波纹管波峰上相邻的两节点，N为网套上任一节点，N1′、N2′和N′分别为N1、N2、N变形后的点，UX1、UX2、UX分别为点N1、N2和N的径向变形，则节点N的径向位移UX可由节点N1、N2的径向变形UX1，UX2来表示，由平面几何的基本知识得到其表达式为：

其中D1表示N与N1之间的距离；D2表示N与N2之间的距离。

2.3 扩展部分

扩展部分从凝聚解结果开始，计算超单元中所有自由度。读入生成部分的数据库，进入求解器，激活扩展选项，选择要扩展的超单元名，利用使用部分生成的凝聚解，开始求解，就得到超单元完整解。用子结构技术建立的金属软管的有限元模型如图5所示。

3 算例分析

下面以一个QPB-S50×190型双层金属软管为例，利用已建立的参数化有限元模型对其静力学性能进行仿真分析。该金属软管的材料为1Cr8Ni9Ti，弹性模量E＝196MPa，塑性模量Ep＝257MPa，屈服强度s＝257MPa，密度 ＝7.8×103kg/m3，泊松比 ＝0.3，金属软管的几何尺寸如表1所示。

图5 金属软管的有限元模型

表1 金属软管的几何尺寸

3.1 轴向刚度

载荷施加方式采用一端固定，另一端施加位移的方式，测得支反力-位移之间的关系曲线，即为金属软管的轴向刚度曲线。拉伸和压缩状态下金属软管的轴向刚度曲线分别如图6和图7所示。表2给出了试验值、利用普通有限元模型计算的支反力，以及利用子结构技术建立的有限元模型计算的支反力的比较。从表2可以看出，利用子结构技术建立的有限元模型比普通模型计算的值与试验值更加接近，验证了模型的可靠性，同时计算时间大大减少了，对计算机的设备要求也降低了。

表2 金属软管的几何尺寸

图6 金属软管拉伸时的轴向刚度曲线

图7 金属软管压缩时的轴向刚度曲线

从图6和图7可以看出：金属软管在承受轴向压缩时，其轴向刚度基本呈现线性规律，且在与拉伸产生相同的变形时压缩力要少得多，说明了金属软管轴向压缩性能好于轴向拉伸性能。

3.2 横向错动

此时的边界条件和受力情况为：金属软管左端所有节点自由度完全固定，右端径向自由度UX放开，施加横向力UX=7mm，其余自由度固定。经有限元分析程序计算后，得到横向力-位移曲线如图8所示。

图8 金属软管横向错动的力-位移曲线

图8表明：金属软管在横向错动曲时，其相应刚度大体上呈现线性规律。经有限元分析计算证明，沿各个方向的错动其刚度大致是相同的，但实际上由于制造工艺的影响，各个方向的错动刚度实验值有所差异，但均呈现线性规律。

3.3 自由弯曲

此时的边界条件和受力情况为：一端固定，另一端施加自由弯曲角度5°。得到力-弯曲角度之间的关系曲线如图9所示。

图9 金属软管自由弯曲的力-角度曲线

图9表明：金属软管在自由弯曲时，其轴向刚度（FZ曲线）和径向刚度（FX曲线）大致呈现线性规律。

3.4 多载荷工况

在实际工作中的金属软管往往不仅仅受某个载荷单一作用，而是在各种载荷联合作用下工作，下面研究金属软管在承受内压、轴向拉伸和横向错动载荷综合作用下的静力学特性。此时约束情况为：左端所有节点自由度完全固定，右端施加轴向位移DZ=7.2mm，横行位移DX=7mm，内压1Mpa，经有限元分析程序计算后，得到其Von Mises等效应力分布云图如图10所示。

图10表明金属软管在承受内压、轴向力和横向力的综合作用下，最大应力发生在波纹管的波谷处，这一结论与实际情况比较吻合，进一步证明了利用子结构技术建立的有限元模型的可靠性。

4 结论

利用子结构技术，在ANSYS中建立了金属软管的有限元模型，通过对金属软管在轴线拉伸、轴向压缩、横向错动、弯曲和多种载荷联合工况下的静力学性能进行了有限元法分析，并将分析结果与试验值进行了对比，证明了有限元建模的准确性。利用子结构建立的有限元模型大大缩短了计算时间，降低了对计算机设备和内存的需要。本文的研究成果对准确把握金属软管的静力学性能有重要的实用价值，为金属软管的动态特性分析提供了可靠的有限元模型，为金属软管的使用和设计提供了有价值的参考。

图10 多载荷工况下金属软管的Von Mises应力云图

[1] 葛子余. 金属软管[M]. 宇航出版社, 1985: 1-48.

[2] GB/T 12777-2008, 金属波纹管膨胀节通用技术条件[S],2008.

[3] 马少坤, 于淼, 崔皓东. 子结构分析的基本原理和ANSYS软件的子结构分析法[J]. 广西大学学报(自然科学版),2004(6): 150-153.

[4] 田涌涛, 李从心. 基于子结构技术的复杂齿轮系统有限元三维接触分析[J], 机械工程学报, 2002(5): 133-137.

[5] 荀兵. 子结构法在有限元线性静力分析中的应用[J], 矿山机械, 2003(2): 47-49.