复连通二维Stokes问题的Galerkin边界元解法

王小军，刘晓宇，杜亚楠

(重庆大学数学与统计学院，重庆 400030)

边界元方法是求解不可压缩粘性流体Stokes流动问题数值解的理想方法。对于二维问题，在区域的边界是封闭曲线的情况下，如无界流体的绕流问题或有界固壁容器中流体的流动问题等Stokes问题，用边界元方法求解已有丰富的研究成果，然而多侧重于理论分析。本文拟对复连通二维Stokes问题的Galerkin边界元解法中的程序设计等技术性问题进行探讨。

根据Green公式和Stokes算子的基本解可以推导出对应于复连通闭曲线Stokes问题的边界积分方程，得出基于单层位势的间接边界积分方程，这是一个第1类的Fredholm向量积分方程。对与之等价的边界变分方程采用Galerkin边界元求解，得出单层位势的向量密度，进而得出流场中任意点的流速值。本文主要讨论其中用利用Fortran计算所求点的流速与用Matlab画出相应的流线图的主要过程。

1 复连通区域Stokes问题的边界积分方程

设Γ1是R2中有限区域Ω的封闭曲线，Γ2是Γ1形成的封闭区域中的一条封闭曲线，Γ2形成的区域为 Ω0+，Ω0－=Ω －Ω0+。设 Γ=Γ1+Γ2，考虑如下的问题:

其中:u=( u1，u2)是流速;p是压强;u0是闭曲线边界Γ1以及内部闭曲线边界Γ2上的已知函数。

图1 研究区域

设想包含在Ω内的不可压缩粘性流体整体嵌入在平面无限域上的不可压缩粘性流体之中。本文只计算有界域上的流动，故假定在无穷远处流速为零。由参考文献［5］，经计算可得到基于单层位势的边界积分方程:

其中 t= ( t1，t2)是待定的密度函数，其分量ti是穿越Γ时的跃变。类似地可推出流体压力场的积分表达式，但本文约去压力场的计算。

2 变分方程的形成及处理

2.1 形成变分方程

由单层位势出发来研究边界量u0和边界量t的关系，由于u在穿越边界时的连续性，从式(2)得到联系已知函数 u0和中间变量 t的积分方程组:

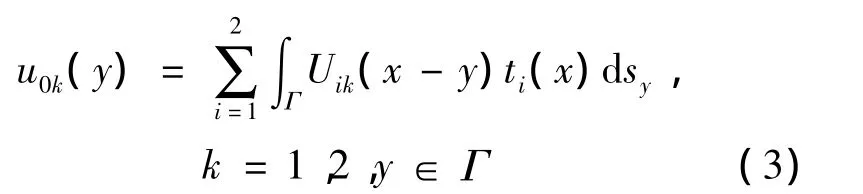
对于方程(3)，方程两边同乘以 t '(y)，然后在Γ上积分，便得到变分方程组:

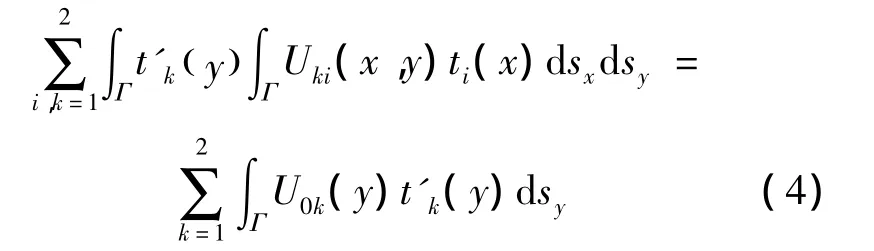
2.2 离散变分方程

为了数值求解变分方程(4)，边界Γ必须离散为一系列单元，从而把边界积分方程转化为线性代数方程组进行求解。设把边界Γ1离散为n1个单元，有单元端点n1个;把边界Γ2离散为n2个单元，有单元端点 n2个，则边界 Γ共划分为 n( n =n1+n2)个单元，共有n个单元端点。在实践中，边界单元一般被离散为常单元、线性单元或者高次单元，也有采用样条插值方式的边界单元。在本文中，采用线性单元就二维问题进行计算。基函数选取如下:

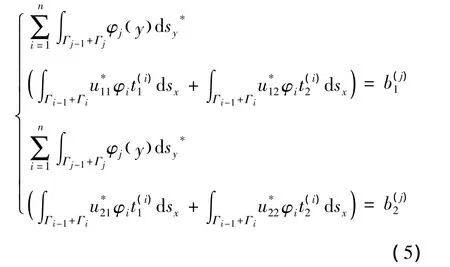
其中:

把上述线性方程组写成简洁形式:AU=B，其中:

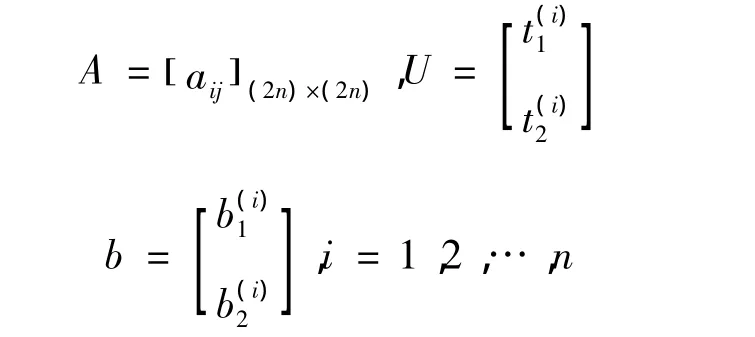
2.3 变分方程中重积分的处理

要求解上述线性方程组(5)，最主要的问题是求解系数矩阵。然而由于积分存在奇异性，若采用数值积分，必然产生较大的误差。为了避免出现这样的问题，在求二重积分时，第1重积分存在奇异性时采用精确解析积分，不存在奇异性时以及第2重积分采用Gauss数值积分。在利用Gauss数值积分计算第2重积分时，对于以闭曲线为边界的区域问题而言，基函数无奇异性，可以方便的使用通常的Gauss数值积分公式。解析公式的推导方法与具体公式见参考文献［2］。利用边界积分方程得到密度函数后，将其数值带入解的表达式即得流速。

3 程序设计

鉴于不同程序设计语言的优势，程序采用两种语言，首先用Fortran计算出所求点的流速，保存结果在文本文件中，然后用Matlab读取画出流线图。

Fortran程序采用模块化设计，包括主程序MIAN以及8个子程序，其中主程序控制程序的执行顺序，采用多个输入输出文本文件读取写入以便于与Matlab结合。在主程序中设置全局变量，包括了边界点，边界点对应的流速，边界单元长度，稀疏矩阵，右端项，单层位势的向量密度，所求点的坐标以及所求解。

在输入功能子程序INPUT中要实现的功能是输入边界节点坐标、已知边界条件和所需计算的内点坐标。

在形成系数矩阵的子程序FMAT中，首先通过两层循环采用4点Gauss数值积分公式形成右端项，然后通过3层循环调用解析积分公式和4点Gauss数值积分公式形成系数矩阵，其中在第1层积分中，存在奇异性时调用解析积分公式，不存在奇异性时调用4点Gauss数值积分公式。

计算解析积分公式的子程序FUN中，通过判断语句根据积分源点到有向线段的距离是否为零分情况计算系数矩阵对应元素的数值。

计算4点Gauss数值积分公式的子程序，调用为Gauss数值积分作准备的子程序，将坐标转变为无因次积分点坐标，实现非奇异情况下的数值积分。

计算线性代数方程组的源程序，采用列主元消去法求解边界积分方程组。

计算流速的子程序中采用2层循环，将求得的密度数值带入解的表达式求得未知点的流速及其方向。

输出结果的子程序将计算出的结果写入文本文件，以便对比和画流线图。

Matlab程序中首先对区域进行剖分，得到所求点坐标，将坐标输出到文本文件，由Fortran程序计算出流速后，加载并读取保存结果的文本文件，然后调用已知函数画出流线图，最后画出边界并确定坐标名称。

4 数值算例

算例1 单位圆流速为(0，0)，矩形区域［－5，5，－10，10］边界上的速度为(1，0)，计算矩形内单位圆以外的点的流速并画出流线图。

在此算例中，内部圆边界划分为16个单元，外部闭曲线划分为60个单元，边界总剖分为76单元，由Matlab剖分在矩形区域内确定 1 521个点，除去圆内部余1 492个有效点，由Fortran程序计算出流速后输出到文本文件，耗费时间以秒为单位，再由Matlab程序读取画出流线图，耗费时间也是以秒为单位，与其他方法计算结果相对比精度较高，画出的流线图与实际情况符合很好(图2)。

图2 算例1流线图

算例2 单位圆流速为(0，0)，矩形区域［－5，5，－10，10］边界上的速度为

计算矩形内单位圆以外的点的流速并画出流线图。

在此算例中，边界剖分与计算流程与算例1完全一致，计算、画图耗用时间以及结果精确度也完全一致(图3)。

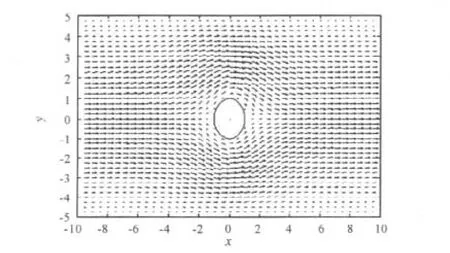
图3 算例2流线图

算例3 单位圆流速为(0，0)，矩形区域［－5，5，－10，10］边界上的速度为计算矩形内单位圆以外的点的流速并画出流线图。

在此算例中，边界剖分与计算流程与上述两例完全一致，计算、画图耗用时间以及结果精确度也完全一致。不同点在于，Matlab画图中放大后将清晰的出现2个小的漩涡。漩涡如图4所示。

图4 算例3的漩涡图

通过以上数值算例可以看出，该种方法精度较高，计算结果符合客观事实。

［1］Hsiao G C.A modified Galerkin scheme for equations with natural boundary conditions［C］//Vichnevetsky R，Vigness J.Numerical Mathematics and Applications.B.V:Elsevier Science Publishers，1986:193 －197.

［2］向瑞银.平面定常Stokes方程的Galerkin边界元解法［J］.重庆大学学报，2006(2):29－30.

［3］张耀明，温卫东.平面定常Stokes问题的无奇异第一类边界积分方程［J］.计算数学，2005，2(1):1－10.

［4］祝家麟.椭圆边值问题的边界元分析［M］.北京:科学出版社，1991.

［5］祝家麟.定常Stokes问题的边界积分方程法［J］.计算数学，1986(8):281－289.

［6］Zhu Jialin.The boundary integral equation method for solving stationary Stokes problems［C］//Feng Kang.Proc.of the 1984 Beijing Symp.On Diff.Geometry and Diff.Equations.Beijing:Science Press，1985.