对称12弹性振子的二维非线性振动

包兴明，张 豪

(1.四川理工学院理学院，自贡 643000;2.电子科技大学数学科学学院，成都 611731)

现实中考虑各种因素后，物体所做的各种振动几乎都是非线性振动。非线性问题是当前物理研究中的热门问题，但其求解具有极大难度，除了少部分特殊情况可以用解析法解决以外，大部分问题要依靠数值方法，利用计算机才能得出其结果。文献［1］分析了几种常见的线性弹簧组合，对作非线性振动弹簧振子进行了数值求解，并与通过计算得出解析解进行了对比，解析解与数值解是一致的。但目前对实际生活和生产中常见的二维非线性振动少有所研究［2］。本文应用拉格朗日方程方法并用数值计算研究弹簧系统中对称12弹性振子的二维非线性振动，给出其非线性振动方程并给出振动曲线。

1 对称12弹性振子的运动方程

对称12弹性振子的物理模型可以用一个在光滑水平面上运动的质量为m的质点来描述，它与12个弹性系数均为k、原长均为a的弹簧相连。在平衡时这12个弹簧互成30°。这12个弹簧两两对称，此时弹簧为原长，质点在xy平面内(水平面)作微小振动。以质点的平衡位置为原点o，建立坐标系oxy，如图1所示。

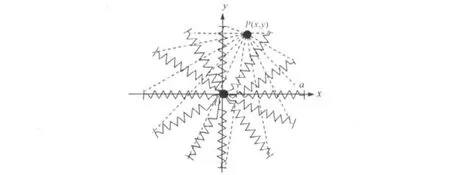
图1 对称12弹性振子

系统的动能和势能分别为

系统的拉格朗日函数为

根据保守力系统的拉格朗日方程

得到系统的运动微分方程为

方程(5)与方程(6)是一非线性耦合方程组［3］，这表明弹簧振子的运动是非线性振动。线性弹簧在此种组合下，由于其势能函数V(x，y)不再是二次函数，必然产生非线性振动。其振动形式的解析解很难直接得到，本文采用数值方法对其进行研究。

若振子作微小振动，则方程(5)可化为

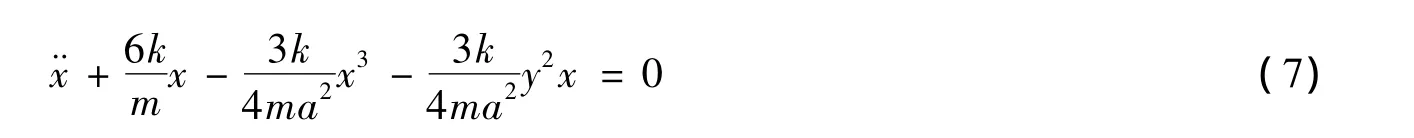
这是一个软非线性的微分方程［4］，它给出了一个恢复力为x3的非简谐振动的物理力学模型。若振子作微小振动，则方程(6)可化为

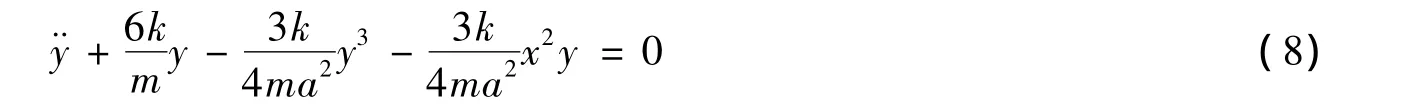
这是一个软非线性的微分方程［4］，它给出了一个恢复力为y3的非简谐振动的物理力学模型。

2 振动的数值求解和振动曲线模拟

为简单起见，假定该弹性振子质量m=1 kg，弹簧原长为a=1.0 m，弹性系数k=0.1 N/m。现在，用数值方法研究系统在给定初始条件下的响应。

1)初始条件为x0=y0=0.05 m==0.0 m/s。利用maple语言的超强数值计算功能［5］，在如上的条件下，求解方程(5)和(6)，得到x，y方向的振动曲线(图2)，x方向振动和y方向振动的振幅均为 0.049 989 560 776 723 951 4 m。

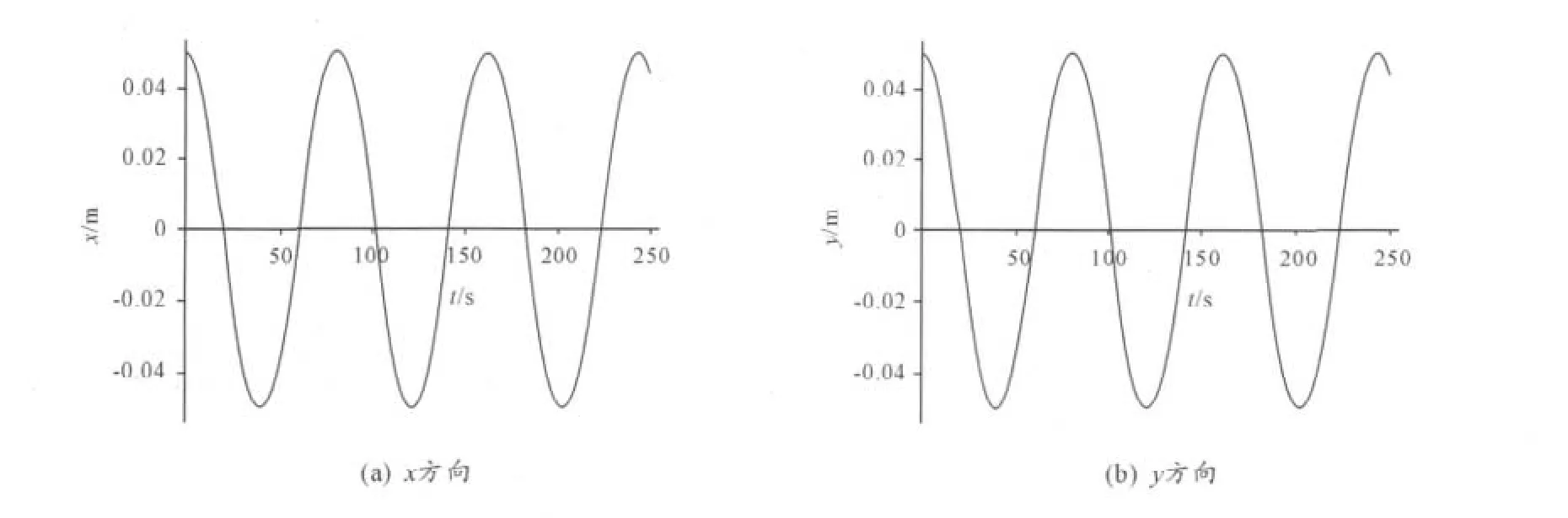
图2 x0=y0=0.05 m=0.0 m/s时的振动曲线

2)在x0=y0=0.05 m=0.03 m/s=－0.03 m/s的初始条件，求解出方程(5)和(6)，得到x，y方向的振动曲线(图3)，x方向振动的振幅为0.063 241 716 209 257 073 4 m、周期为81 s，而y方向振动的振幅为0.063 227 956 503 896 926 0 m。

图3 x0=y0=0.05 m=0.03 m/s=－0.03 m/s时的振动曲线

3)在x0=y0=0.1 m的初始条件，求解出方程(5)和(6)，得到x，y方向的振动曲线(图4)，x方向振动和y方向振动的振幅均为0.099 956 279 830 978 711 6 m。

图4 x0=y0=0.1 m0.0 m/s时的振动曲线

4)在x0=y0=0.1m=0.03 m/s=－0.03 m/s的初始条件，求解出方程(5)和(6)，得到x，y方向的振动曲线(图5)，x方向振动的振幅为0.107 377 121 537 032 590 m、周期为81 s，而y方向振动的振幅为 0.107 072 704 126 938 560 m。

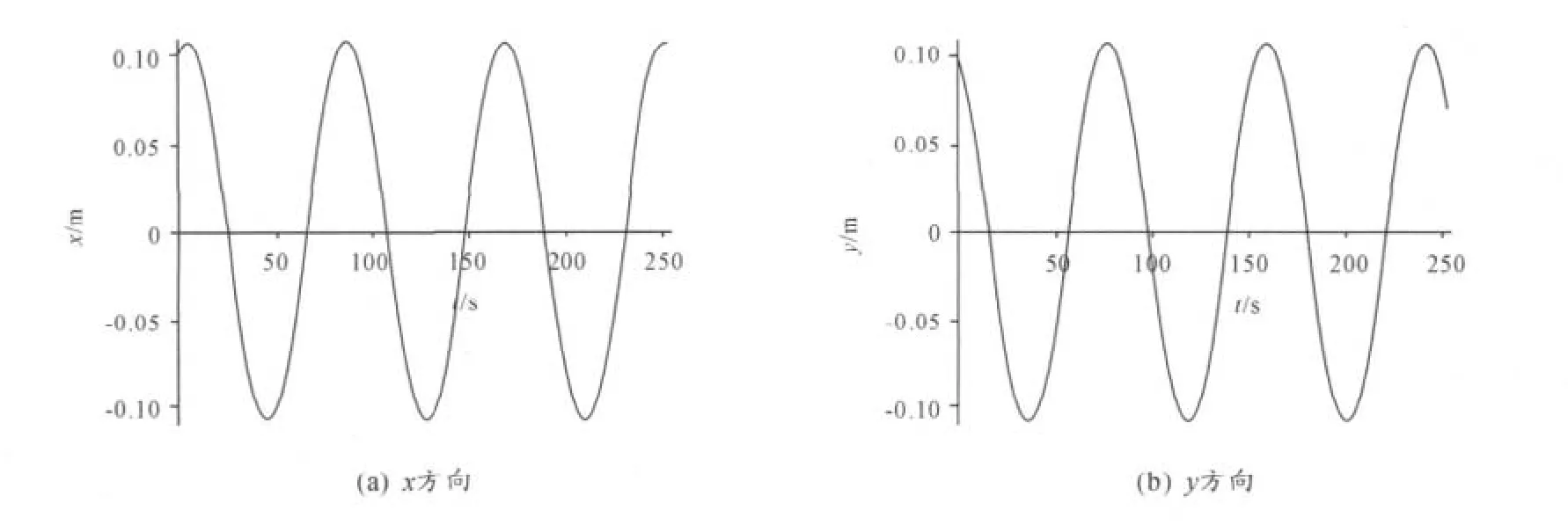
图5 x0=y0=0.1 m=0.03 m/s=－0.03 m/s时的振动曲线

由图2～5可以看出:

1)在微小振动的条件下，对称12弹性振子的振动是非简谐的周期性振动;在保守力系统中，非线性振动系统的振幅与初始位置和初始速度有关系。初始位置增大，振幅增大;初始位置不变，若初始速度增大，则振幅也增大。

2)在其x方向和在y方向的振动曲线都可以看成是一个形变了的余弦曲线，其上附加有依赖于振幅的高频颤动。

3 结束语

对弹簧系统中常见的二维非线性振动问题，可利用拉格朗日方法得到其振动控制微分方程，借助于计算机和maple语言在计算方面的超强功能，成功解决了该类非线性振动问题。这种方法有效简便，这就为非线性问题探索出了一种极好的求解途径。

振动曲线彼此相似，其波形与振幅无关，具体形状介于余弦波和三角波之间，可以看成是一个变形了的余弦波，其上附加有依赖于振幅的高频颤动。

［1］廖旭，任学藻.组合线性弹簧振子中的非线性振动［J］.大学物理，2008，27(2):25－28.

［2］包兴明，周志坚，袁玉全.弹簧系统一种常见的二维非线性振动［J］.西南师范大学学报，2008，33(4):28－31.

［3］卓崇培.非线性物理学［M］.天津:天津科学技术出版社，1996:26－61.

［4］刘式适，刘式达.物理学中的非线性方程［M］.北京:北京大学出版社，2000:6，66.

［5］黎捷.MAPLE 9.0符号处理及应用［M］.北京:科学出版社，2004.