基于Boosting的网络异常流量检测算法研究

于振洋

(淮阴工学院计算机工程学院，江苏 淮安 223003)

0 引言

随着互联网技术的发展，计算机网络业务也呈现出多元化的趋势。在网络规模不断扩大的同时，出现了数据流量过大导致网络拥塞、恶意攻击等网络崩溃现象，因此，网络流量预测在现代网络中具有重要作用。进行流量预测能够使人们实时监控网络流量，在网络性能出现恶化之前采取相关遏制措施。

网络流量预测一直是研究的重点问题，目前已提出许多预测模型和算法。这些预测模型和算法主要分为:基于自回归或自回归滑动平均的预测模型、基于自回归综合滑动平均的预测模型、基于分形自回归综合滑动平均的预测模型、基于神经网络的预测模型、结合小波变换和小波分析的预测模型及综合小波与神经网络的预测模型。当人获得指导信息时，如何利用这种信息，来进一步提高算法的性能是一个值得研究的课题。流量分析的基础是对流量的测量，如何利用分析所得结果，反过来指导主动式测量的进行，也是非常有意义的课题。

1 基于Boosting的学习算法

Boosting是一类使得弱学习算法的性能得以提高的学习策略。基于Boosting的学习算法的思路如下:如果要想找到许多条简单粗略的判断准则要比找到一条非常精确的准则容易得多，在Boosting算法中，通过不断调用这种“弱的”或“基本的”学习算法，每次用训练样本的不同子集对它进行训练(更确切地说，是训练样本的不同分布或权重)，每次被调用时，基本的学习算法将产生一条新的弱的判断准则，循环多次后，Boosting算法必须把这些弱的准则结合成一条准则，该准则很可能比弱准则中任何一条都要精确得多。

以处理二分类问题的ADA－Boost为例，得到基于Boosting的学习算法流程如下:

ADA－Boost算法流程:

(1) 给定训练集(x1，y1)，…，(xm，ym)，其中，xt∈ X={－1，+1}，yt∈{－1，+1}。

(2)初始化样本权重分布D1(t)=1/N(t=1，…，N)。

(3)迭代过程在每一轮迭代中t(t=1，2，…，T):

(a)利用分布Dt训练一个弱分类器;

(b)得到弱分类器ht:X→R;

(c)计算弱分类器的训练误差st=Prt－Dt［ht(xt) ≠ yt］;

(d)计算弱分类器重要性αt∈R;

(e)更新样本权重分布。

在理论上，ADA－Boost算法的训练误差的界由下式给出:

其中，f(x)=∑αtht(x)。从上式可知，只要保证在每一轮迭代中，弱分类器的效果比随机猜测要好一点，Boosting算法的训练误差就会随着迭代步数的增加呈指数下降趋势。从这个角度看，Boosting算法有效地将一个弱学习算法转化成一个强学习算法(给定足够多的数据，能产生一个错误率任意的分类器)。

关于ADA－Boost的推广误差，文献［7］已经分别给出了几种不同形式的上界，从而在理论上给出了ADA－Boost有效性的一些解释。

目前，基于Boosting的算法主要应用在监督问题(大多数情况下是二分类问题)和异常网络流量监测中，本文将主要研究其在非监督情况下的应用。

2 基于Boosting的异常流量检测算法

本节研究基于Boosting的异常流量检测算法，首先给出基于ADA－Boost的算法流程，然后讨论算法的各个实现细节。本文提出两种不同形式的弱学习算法设计方式以及相应的误差评价分析:估计多变量高斯分布以及估计超球体区域，在前一种策略中，假定正常流量的分布是一种多变量的单高斯分布;在Boosting算法的每一轮迭代中，估计多变量高斯分布根据样本的当前权重分布，估计高斯分布的均值向量和协方差矩阵，这种方法属于基于概率密度估计的方法。在后一种策略中假定正常流量聚集在一个超球体内部;在Boosting算法的每一轮迭代中，估计超球体区域根据样本的当前权重分布，估计超球体的球心和半径，这种方法属于基于置信区域估计的方法。

2.1 算法流程

根据ADA－Boost算法的一般流程，很容易得到基于Boosting的异常网络流量检测算法流程:

(1)从网络流量历史数据中，建立训练集D={Xt，t=1，…，N} ∈Rm，N为原始训练集D中所有样本的总数。

(2)初始化训练集样本的权重:D1(t)=1/N。

(3)重复如下迭代过程，直到终止准则满足，在每一轮迭代中 t(t=1，2，…，T):

(a)根据样本的当前权重分布Dt，在训练集D上训练一个弱学习算法;

(b)得到一个弱学习算法:Rp→R;

(c)利用所得到的弱学习算法:评估训练集D中每一个样本t的误差信息lt(t);

(d)计算弱学习算法的训练误差st;

(e)选择系数αt∈R，以衡量弱回归算子的重要性;

(f)更新训练集D中样本的权重分布:Di→Di+1;

(g)判断终止准则是否满足。

(4)组合上述过程中得到的弱学习算法的输出:{{ht，t=1，2，…，T} → H}。

(5)对于测试数据xtest∈Rm，根据第(4)步的输出结果，判定其是否为异常情况。

2.2 设计弱学习算法

在本文中设计了两种形式的弱学习算法:

(1)估计多变量高斯分布

这种情况下假定正常流量的分布是一个多变量的单高斯分布N(μ，∑)，在第t轮的迭代中，参数μ和∑分布通过公式(1)和公式(2)确定:

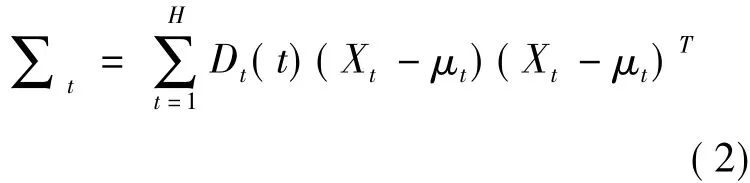
对于任一样本，其在估计多变量高斯分布(MGE)条件下的输出可通过样本的概率密度表示:

(2)估计超球体区域

假定正常流量聚集在一个超球体内部，假设估计超球体区域的球心为μ，采用马氏距离来衡量任意一个点X到球心的距离:

在第t轮的迭代中，参数μt和∑t同样通过公式(1)和公式(2)确定。为了确定超球体的半径r，在指定虚警率的情况下，通过假设—校验的方法来确定，或者简单地将其设置为一个常数。对于任何一个样本，其在估计超球体区域的输出表示为:

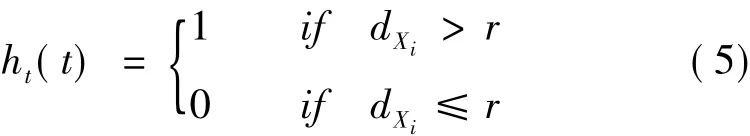
2.3 评价样本的误差信息

在得到一种弱学习算法以后，需要评价训练集中的每一个样本的误差信息。无论采用哪一种弱学习算法(估计多变量高斯分布或估计超球体区域)，误差信息用下式来评价:Lt(t)=1－ht(t)，如果Lt(t)表示在第t轮迭代中第t个样本的误差信息，得到各个样本的误差信息以后，弱学习算法的误差由下式计算得到:

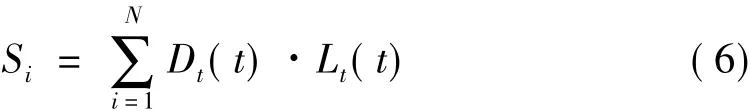
为了权衡弱学习算法的重要性，采用和ADA－Boost一样的策略为

2.4 算法设计

(1)更新权重分布

采用和ADA－Boost算法相同的样本的权重分布更新策略:

其中，Zt是以规整化的系数，以保证Dt+1(t)是一种数据的分布形式。

(2)算法终止准则

在理论上，ADA－Boost算法在εt≥0.5时终止，为了避免εt长期停留在0.5附近，在本文中设置一个最大迭代步数Tmax。这样，算法的终止准则可由公式(8)给出:

(3)组合弱回归算子输出

为了得到算法最终的输出，设定采用中值方式组合弱学习方法的输出:

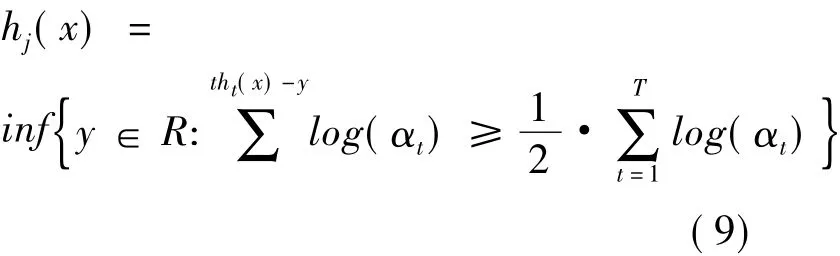
(4)判定流量正常与否

对于某一个测试数据Xtext∈Rm，用公式(8)得到输出值hj·(Xtext)，如果hj·(Xtext) ≥c，判断样本正常，否则判断样本异常，参数c通过预设的虚警率确定:

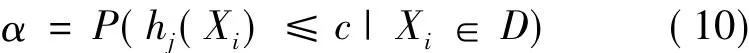
3 实验结果及分析

3.1 实验过程

实验环境为Matlab 2009b，在实验中我们采用经典的DARPA 1999 Data Set，该数据集持续时间为7个星期，数据大小为10G，包括54种攻击，该数据集提供的文档说明每一起攻击事件的类型、发生和结束时间以及包含的主机，每一种攻击还有一个类标志，DARPA入侵检测数据库一共有四个类型:R2L(Remote To Local)、U2R(User To Root)、DOS(Denial Of Service)、PROBE，R2L 是远程用户获得本地用户权限攻击，U2R为本地普通用户获得超级用户权限攻击，R2L、U2L的攻击可能会破坏网络和系统的保密性、完整性和认证，DOS为拒绝服务攻击，破坏系统的可用性，PROBE为试探攻击，破坏系统的机密性，并给其它攻击类型提供信息。

通过实验，获取整个数据集中的第一周数据:Tue和 Wed数据不含任何形式的攻击(Attack Free)，用来构成训练数据集D;Thu和Fri数据含有若干形式的攻击(如表1)，用来构成测试数据集，文献［8］提出的一类SVM方法，被用来与本文算法作比较。

表1 DARPA 1999 Data Set第一周的攻击类型信息

图1 基于Boosting的算法和OCSVM ROC结果比较

基于Boosting的算法中，相关参数和操作设置如下:

(1)每个样本的持续时间(Duration)分别设为60s、120s、180s、300s;

(2)将应用估计超球体区域当作弱学习算子时，超球的半径确定的方法为:每次迭代，使得球内的样本数目占训练集样本总数的95%;

(3)最大迭代步数Tmax设为30。

3.2 基于Boosting的实验结果和分析

在测试集上的ROC(Receiver Operating Characteristic)结果如图1所示。

ROC曲线是查准率随虚警率(False Alarm Rate)变化的曲线，其中，圆圈表示使用Boosting(弱学习算法为估计多变量高斯分布)的检测结果(MGE)，正方形表示使用Boosting(弱学习算法为估计超球体区域)的检测结果(HBE)，三角形表示使用一类支持向量机(OCSVM)的结果。从图1中可知，基于Boosting的检测算法总要优于OCSVM。

通过比较两种不同的弱学习算法可知，如果样本的持续时间(Duration)较短(60s、120s)，那么虚警率较低(＜10%)时，估计超球体区域的性能要优于估计多变量高斯分布;当虚警率较高(＞10%)时，估计多变量高斯分布的性能要略优于估计超球体区域。另一方面，如果样本的持续时间(Duration)较长(180s、300s)，那么两种机制的性能基本相当。

4 结论

本文将Boosting算法引入到异常网络流量的检测当中，设计了两种不同的弱学习方法:估计多变量高斯分布和估计超球体区域。实验结果表明，基于Boosting的检测算法性能要优于OCSVM。这表明Boosting作为一种提升弱学习算法性能的一般性策略，在非监督情况下是十分有效的。

［1］Mohammad Assaad，Romuald Boné.A new boosting algorithm for improved time－series forecasting with recurrent neural networks［J］.Information Fusion，2008，9(1):41－55.

［2］Michael Kearns，Leslie G.Valiant.Cryptographic limitations on learning Boolean formulae and finite automata［J］.Journal of the Association for Computing Machinery，1994，41(1):67－95.

［3］［7］Michael C.Mozer，RichardWolniewicz，David B.Grimes，et al.Predicting subscriber dissatisfaction and improving retention in the wireless telecommunications industry［J］.IEEE Transactions on Neural Networks，2000(11):690－696.

［4］［8］Keerthi S S，Lin C J.Asymptotic behaviors of support vector machines with Gaussian kernel［J］.Neural Computation，2003，15(7):1667－1689.

［5］赵秀丽，赵俊龙.基于局部相关性的L2Boosting算法［J］.计算机工程，2010，36(8):1－3.

［6］钟向阳，凌捷.基于多阈值Boosting方法的人脸检测［J］.计算机工程，2009，35(11):172－174.