基于改进型DDS的函数发生器设计

倪桑晨

(东南大学信息科学与工程学院，南京 211189)

0 引言

频率合成技术分为直接数字频率合成技术(Direct Digital Synthesizer，DDS)、间接频率合成技术、直接模拟频率合成技术。其中，直接数字频率合成技术是一种新的频率合成技术，它具有频率分辨率高、频率切换速度快、相位切换连续、可输出任意波形信号、输出信号相位噪声低、易于集成、体积小、重量轻等优点。因此，本文基于微处理器及改进型DDS提出了函数发生器的设计方案，它与由模拟振荡器和锁相环(PLL)组成的系统相比，硬件要求低、控制灵活、快速性好且频率分辨率高，能实现输出波形频率、幅值的步进可调，所阐述的合成波形波表生成算法方便地实现了各种复杂波形的调频、调幅和调相功能。

1 系统总体设计

基于微处理器与DDS的函数发生器由STC12C5A16S2微处理器、DDS模块、双端口数据存储模块、D/A转换模块、波形频率/相位/幅值控制模块、键盘扫描模块、LCD液晶显示模块、电源监控与复位电路、滤波及稳幅模块等组成。改进型DDS架构负责将双端口数据存储器中的波形数据按相应频率间隔周期性地送到D/A转换器的输入端，从而在D/A转换电路的输出端得到相应的电压波形，而微处理器STC12C5A16S2采用增强型8051内核，速度是普通8051的8～12倍，且内置16Kflash、1280片内SRAM，主要负责输出波形的量化数据、幅值和频率控制字的计算，并负责波表的生成、移植以及实施相应地控制。其总体设计框图如图1所示。

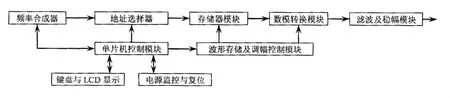
图1 总体设计框图

2 系统硬件设计

2.1 DDS 技术实现

传统的DDS主要由标准参考频率源、相位累加器、波形存储器、数模转换器、低通平滑滤波器组成，在时钟脉冲的控制下，频率控制字由累加器获得相应的相码，相码在寻址波形存储器中进行相码—幅码变换，输出不同的幅值编码，经数模变换输出相应的阶梯波，然后经低通滤波器对阶梯波进行平滑处理，即得到由频率控制字决定的连续输出的波形。考虑到系统输出波形频带范围为0.01Hz～1KHz，频率分辨率为 0.01Hz，且为了确保输出波形质量并满足相位的调整要求，每周波由1024个分布均匀的波形量化数据组成。因此系统选用频率分辨率较高的数字式频率合成器AD9850作为参考时钟源，同时采用计数器寻址结构取代传统DDS中的累加式寻址结构，在没有微处理器干预的情况下实现波表数据的自动输出，即每隔一个参考时钟脉冲，地址计数器自动加1，此计数器产生的计数值直接作为波形数据表RAM的寻址地址。

AD9850芯片输出频率fout由公式(1)决定。

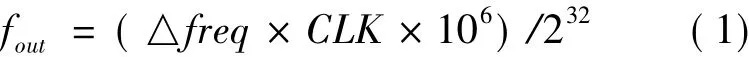
其中，fout的单位为Hz;CLK为DDS芯片工作频率，系统选用16.384MHz，△freq为32位频率控制字。若输出波形基频为f，则地址计数器计数频率应为波形频率f的1024倍，则由公式(1)可推导出AD9850相应的频率控制字为:

图2 DDS与波形存储器电路

具体电路原理如图2所示。其中，AD9850每隔1024*f产生一个脉冲信号，此信号经QN输入级联计数器4024，此计数器产生的计数值直接寻址双端口RAMIDT7132，用于获取当前相位所对应的波形采样点的幅值量化数据，并实现D/A转换，经低通滤波及驱动放大电路获取所需波形。当地址计数器累计满1024次时，AC有效，级联计数器自动复位，计数器开始新的周期计数，同时在模拟量输出端口将形成完整的1024个波形量化数据，其波形频率则为f。

2.2 波形存储器控制

为了确保输出波形质量，提高波形输出速度，有效解决波形输出时因CPU资源被占用而无法及时处理突发事件的问题，本设计采用双端口RAM与计数器相结合的方式实现波形的连续输出。系统选用存储容量为2K的IDT7132双端口RAM作为波形数据存储器，左端口与微处理器相连，右端口A0R～A9R地址总线直接与级联地址计数器U4、U5的输出端Q1～Q7、Q1～Q3相连，I/O0R～I/O7R经锁存器输出至DA转换电路中的U16数据端DI0～DI7。为了防止微处理器与地址计数器同时寻址双端口RAM，系统通过P1.3以及双端口RAM的片选信号设置了双端口RAM访问仲裁控制逻辑，如图2所示。当P1.3为高电平且RAM片选信号有效时，RAM左端口有效，允许微处理器执行写操作，将生成的1024点波形量化数据写入RAM;当P1.3为低电平且RAM片选信号无效时，RAM右端口有效，将自动读出指定地址的波形数据供DA模块实现波形转换。

2.3 数模转换及幅度控制

在设计函数信号发生器时，输出信号的幅值分辨率是需要考虑的重要因素之一。本次设计中，模拟信号输出电压范围为－10～10V，幅值分辨率为0.01V，且转换速率要求不高，当参考电压VREF确定后，按输出信号幅值分辨率公式(3)即可计算出DAC字长W，选择DAC0832芯片用于数模转换能完全满足系统要求。

图3 幅度可调D/A转换电路

为了解决输出信号幅值较小时幅值分辨率低的问题，确保系统全量程范围内输出电压分辨率均为2－W(信号电压最大幅值为VREF)，本系统采用两片DAC0832级联来实现幅值的控制，其中一片DAC受级联地址计数器U4、U5控制，周期性地对双端口存储器RAM中存储的波形量化值进行数模转换，而另一片DAC则由微处理器直接控制，输出与设定电压值相对应的幅值数据，并进行数模转换，转换结果作为第一片DAC的基准电压，即VREF，从而在VAOUT、VBOUT输出端得到相应频率、幅值和相位的波形，具体电路如图3所示。

3 系统软件设计

3.1 软件流程图

软件系统包括初始化、DDS模块参数设置、中断处理、D/A转换、幅值 /频率/相位控制字计算、LCD显示、键盘扫描等模块。限于篇幅，本文仅给出系统主程序流程图，如图4所示。

图4 主程序流程图

3.2 波表生成算法

3.2.1 标准波形表

系统可产生正弦波、方波、三角波、锯齿波等标准波形，本文以函数f(t)=Amsinωt为例阐述波形数据表的生成方法，首先确定每周波的采样点数N(N=360/相位分辨率)，并以N对函数进行离散化处理，考虑到正弦波为双极性函数，因此将幅值零点基准平移至DAC模块字长的2W－1处即可得等价式(4)，在此基础上分别计算各采样点量化值并进行归整。其他波形依照同样原理生成。

其中，Am为信号幅值，k=0，1，…，N－ 1，W 为DAC模块的字长。

为了减少微处理器的计算时间，提高运行速度，上述标准波形的波形表已固化于微处理器Flash中，对于初始相位为零的输出，运行时只需将其直接从微处理器中移植到双端口RAM中，而对于初始相位为φ的输出，可依据公式(5)计算偏移量m。

按m规整后的取值点位置将其从微处理器中移植到双端口RAM即可。

3.2.2 合成波形表

合成波形数据是由标准波形按照一定的幅值比例及频率、相位关系进行数字合成得到的，波形表的生成原理和标准波形表的生成原理基本一致，但两者也存在区别，仅以初始相位均为零的基频叠加n倍频正弦波为例(初始相位非零参照标准波形表)，离散化并作平移处理后得等价式(6)、(7)和(8)。

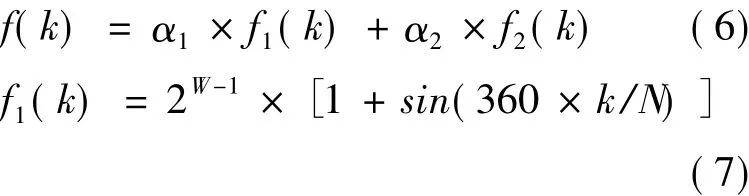
其中，α1、α2为幅值比例系数，α1+ α2≤1，k=0，1，…，N－ 1，n 为倍频数。

当k取1时，f2(1)的量化值即为标准正弦波形母表中n点的值;当k取2时，f2(2)的量化值即为标准正弦波形母表中2n点的值;以此类推，f2(k)的量化值表可由标准正弦波形母表按间隔n－1抽取相应的点值而形成。如果间隔取值采样点数超过了N，则将其与N求余，以余数对应的采样点从母表中取值。在此基础上，将其值乘以系数α2，再与基波f1的离散点值乘以系数α1后的值进行叠加，归整后即可形成函数f(k)的波形表。对于复杂波形，可通过将周期函数展开成为只含常数项、正弦项、余弦项的傅里叶级数，并参照上述方法进行离散化计算，即可获得相应的波形表。需要注意的是，在抽取谐波波形表的过程中，由于标准波形母表中的数据点数不可能被系统所要求的所有谐波次数整除，因此标准波形母表的点数不宜太少，否则将会造成谐波由于一个周期内的数据点数太少而使波形不平滑。

4 结语

基于STC12C5A16S2单片机和改进型DDS设计的函数信号发生器，实现了输出信号类型的选择、信号频率与幅度的数字步进可调等功能，所提出的波表生成算法，有效地解决了相位调节与任意波形表的生成问题。与仅能输出几种固定波形的传统信号发生器相比，具有信号源分辨率高、波形失真小、输出波形任意化等特点，能较好地满足工业控制、医学、科研、教学等对各种低频信号源的要求。

［1］许慧波，张厥胜.直接数字式频率合成器综述［M］.西安:西安电子科技大学出版社，1989.

［2］杨檍，鲍景富.现代频率合成技术的研究进展［J］.电讯技术，2007，47(2):1－5.

［3］黄立新.基于单片机控制的数字函数信号发生器的设计与实现［J］.科学技术与工程，2009，9(12):3278－3282.

［4］于亚萍，刘源，刘华.基于SOPC的DDS函数发生器的设计［J］.工业控制计算机，2009，22(2):65－66.

［5］宋寅.基于FPGA的DDS波形发生器的设计与实现［J］.合肥学院学报:自然科学版，2007，17(2):63－66.

［6］马丽.DDS芯片AD9852及其应用［J］.国外电子测量技术，2003，22(5):6－8.

［7］殷雷，金海军，李映雪，等.基于DDS的高精度函数信号发生器的研制［J］.现代电子技术，2009(1):68－69.

［8］黄乡生，杨占才，胡世文.基于DDS和FPGA的数字函数信号发生器设计和实现［J］.东华理工大学学报:自然科学版，2009，32(4):390－393.

［9］Integrated Device Technology Inc.HIGH－SPEED 2Kx8 DUAL－ PORT STATIC RAM manual［Z］.Integrated Device Technology Inc，2000.

［10］刘进志，陈涤.基于MPU/PLL和CPLD技术的数字正弦信号发生器的设计与分析［J］.山东大学学报:理学版，2005，40(5):88－92.