离散时间单重休假温储备系统的可靠性分析

姜红燕

(淮阴工学院 数理学院，江苏 淮安 223003)

0 引言

以往的可靠性分析理论都是在时间参数为连续的假设条件下讨论的，处理方法通常是微分方程法和拉普拉斯变换法［1］。在实际工程应用中，人们通常定期检测系统、维修或更换部件，这样一来，系统的运行和维修时间等统计量并非是连续的随机变量，而应看作非负整数值的随机变量序列。薛云［2－3］将原有的连续时间模型中的微分方程代之以离散时间的差分方程，研究了可变环境下的离散时间单部件可修复系统的可用度模型;杨懿等［4］分析了离散时间下的单部件可修复系统的可靠性;王金亭［5］研究了离散时间串联系统的可用度模型;余妙妙等［6］讨论了离散时间单重休假冷储备系统的可靠性;梁小林等［7］讨论了单重休假下“修复非新”的情形。

本文在前人工作的基础上，利用离散向量Markov过程方法［8］，提出了一类适用于描述离散时间单重休假温储备系统的状态转移模型，从而得到了系统可靠度、可用度和首次故障前平均时间等可靠性指标。

1 模型的描述

1.1 模型的假设

系统由两个同型部件和一个修理工组成，部件的工作寿命ξ服从参数为p1的几何分布，即:

储备寿命ζ服从参数为p2的几何分布，即:

工作故障的部件和储备故障的部件有相同的修理时间分布，修理时间η服从一般离散型分布，即:

修理工的休假时间τ服从一般离散型分布，即:

发生在休假期间的故障，需等修理工休假结束以后才能得到修理。休假结束后，一旦有故障，修理工立即投入工作，否则，他就是空闲的。先发生故障的部件先修理，另一个则处于等待状态。

当一个部件发生故障时，温储备的部件立即转换为工作状态。转换是瞬时完成的，转换开关是完全可靠的。

所有的部件都能够修复如新。部件的工作寿命、储备寿命、修理时间和修理工的休假时间相互独立。

初始时刻部件都是新的，修理工开始休假。

1.2 模型的分析

此时系统共有10个不同的状态:

状态0:一个部件工作，另一个部件温储备，修理工休假;

状态1:一个部件工作，另一个部件发生工作故障，修理工休假;

状态2:一个部件工作，另一个部件发生储备故障，修理工休假;

状态3:一个部件发生工作故障，另一个部件发生储备故障，修理工休假;

状态4:两个部件都发生工作故障，修理工休假;

状态0＇:一个部件工作，另一个部件温储备，修理工空闲;

状态1＇:一个部件工作，另一个部件因工作故障在修理;

状态2＇:一个部件工作，另一个部件因储备故障在修理;

状态3＇:一个部件因储备故障在修理，另一个部件因工作故障待修;

状态4＇:一个部件因工作故障在修理，另一个部件因工作故障待修。

令N(k)表示系统在时刻k(k=0，1，2，…)所处的状态，显然N(k)不是Markov过程。引进离散补充变量，当 N(k)=0、1、2、3、4 时，令 Y(k) 表示修理工在时刻 k 已用掉的休假时间;当 N(k)=0＇、1＇、2＇、3＇、4＇时，令X(k)表示时刻k正在修理的部件已经修理的时间，它们的取值均为非负整数。

系统在时刻k的状态概率，定义如下:

时刻k已经处于0状态、m时间的概率P0(k，m)=P{N(k)=0，Y(k)=m}

时刻k已经处于0＇状态的概率P0(k)=P{N(k)=0＇}

时刻 k 已经处于 i状态、m 时间的概率 P1i(k，m)=P{N(k)=i，Y(k)=m}，(i=1，2，3，4)

时刻 k 已经处于 i＇状态、n 时间的概率 P2i(k，n)=P{N(k)=i＇，X(k)=n}，(i=1，2，3，4)

2 模型的建立与求解

用概率分析的方法可以得到如下的状态转移方程:初始时刻部件都是新的，修理工开始休假，初始条件为:

其余均为零。

在现代控制理论研究中，Z变换(母函数)是讨论离散时间系统时的一种常用工具。对上述方程组两端进行Z变换，可得:

3 系统的可靠性

3.1 系统的可用度

系统在时刻k(k=0，1，2…)的可用度为:

两端进行Z变换，并将前面所得的结果代入，得

而系统的稳态可用度

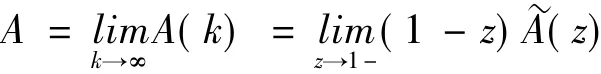
由式(17)以及洛比达法则，可得系统的稳态可用度为:

3.2 系统等待维修的概率

设系统的等待维修概率为P(k)，则:

同理，可得系统平稳状态下等待修理的概率为:

3.3 系统的可靠度

在上述模型中令故障状态 3、4、3＇、4＇为过程的吸收态，令表示系统在时刻 k(k=0，1，2，…) 所处的状态，当N(k)=0、1、2、3、4 时，令Y(k) 表示修理工在时刻 k已用掉的休假时间;当3＇、4＇时，令表示时刻k正在修理的部件已经修理的时间，它们的取值均为非负整数。

系统在时刻k的状态概率定义如下:

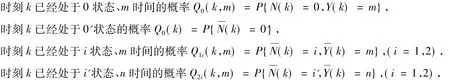
显然，系统的可靠度为:

类似于稳态可用度的求解过程，可得Z变换后的系统可靠度:

4 结束语

本文应用离散向量Markov过程方法，研究了单重休假下的离散时间温储备可修复系统。实际中对很多设备的监控都采用离散参数的分析方法，因而，该研究结果既有重要的理论意义，也有显而易见的现实意义。

［1］曹晋华，程侃.可靠性数学引论［M］.北京:科学出版社，2006.

［2］薛云，曹晋华.可变环境下的离散时间单部件可修系统［J］.系统科学与数学，2006，26(2):178－186.

［3］薛云，曹晋华.可变环境下的离散时间串联可修系统［J］.系统科学与数学，2003，23(2):242－250.

［4］杨懿.离散时间下的单部件可修复系统的可靠性分析［J］.南京理工大学学报:自然科学版，2008，32(4):393－396.

［5］王金亭.离散时间下串联系统的可靠性分析［J］.北方交通大学学报，2001，25(6):81－84.

［6］余妙妙，唐应辉，陈胜兰.离散时间单重休假冷储备系统的可靠性分析［J］.计算机工程与科学，2008，30(10):108－112.

［7］梁小林，莫兰英，唐小伟.具有修理工休假的冷备退化可修系统的研究［J］.系统工程学报，2010，25(3):426－432.

［8］Chaudhry M L，Gupta U.Queue－Length and Waiting Time Distributions of Discrete－Time GIx/Geom/1 Queueing Systems with Early and Late Arrivals［J］.Queuing Systems，1997，25(2):307－334.