直流双转串激永磁电机起动过程分析
杨 洋
(海军驻武汉712所军事代表室,湖北 430064)
1 引言
目前鱼雷推进装置普遍采用直流双转串激永磁直流电机,该特种电机在水下航行器中也被普遍采用[3],研究该型电机的起动过程并计算出准确的起动电流及转速曲线有利于鱼雷电源系统的设计[1],本文对该型电机的起动过程进行了解析计算,并运用仿真工具进行研究。
2 电机起动过渡过程解析计算
该电机的主磁场是由永久磁铁所产生,其磁通 Φ=常数。若忽略电枢反应的影响,等效电路如图1所示[2]。图中La表示电枢绕组的电感与外接电感的总和,称为电枢回路电感;Ra为电枢回路的电阻,Ea为电枢绕组感应电动势;Φs为永久磁铁对外的剩磁磁通。
设电机的静负载转矩为ML,且等于常数。起动前电路处于稳态,即t=0-时,电枢电流Ia(0-)=0。当开关K合闸瞬间,由于电枢回路存在电感La,使得电枢电流 Ia不能跃变。即在t=0+时,Ia(0+)=Ia(0-)=0,所以刚加上电枢电压时,电枢电流为零。当 t≥0时,电枢电流从零开始增大,电磁转矩M(M=CMΦIa)也从零开始增大。当电磁转矩增大到等于静负载转矩(M=ML)时为止,电机一直没有转动。只有当电磁转矩M大于静负载转矩ML时,电机才能加速[5]。因此整个过渡过程分为两个阶段:
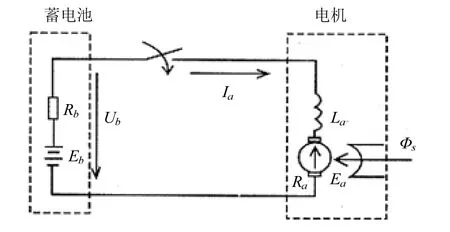
图1 电机等效电路图
1)电动机不转动,电枢电流由零增大IL=MLCMΦ(Φ=ΦN+Φ’), Φ’由 串 励 绕 组 产 生 ,Φ’=KIL这是单纯的电路过渡过程。
2)第二阶段:是运动系统加速和电枢电流变化的过程。因为电动机加速受到机械惯性的阻碍,电枢电流受到电磁惯性的阻碍,所以是机械-电气过渡过程,下面对这两个阶段进行分析。
2.1 单纯的电路过渡过程阶段
图1等效电路中,列出t≥0时的电路的微分方程。
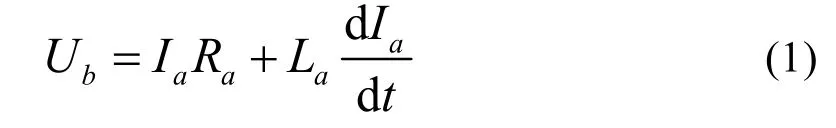
根据换路定则,在t=0+时Ia(0+)=0,则解出电枢电流的过渡过程方程式

式中:Ik=Ub/Ra——短路电流(即制动电流);
τa=La/Ra——电枢电路的时间常数.
式(2)表明:第一阶段中电枢电流按指数规律增长,电枢电流由零增长到IL=ML/CMΦ。所需要的时间可根据式(2)求得如下:

式中:t1——第一阶段的时间;
IL=ML/CMΦ——电磁转矩等于ML时的电枢电流。
第一阶段结束时,电磁转矩已增大到ML,但电路并未达到稳定,电磁转矩还要继续增大,从而使电机开始旋转。因此从电枢通电到电枢开始旋转所需要的时间t1,称为滞后时间。
2.2 机械-电气过渡过程
当过了t1后,电机开始加速,电枢电流变化。因为电动机加速受到机械惯性的阻碍,转速不能跃变;电枢电流受到电磁惯性的阻碍,电枢电流不可能跃变。由于转速变化使电枢电动势Ea=CeΦn随之变化,电枢电动势变化要影响到电枢电流Ia=(Ub-Ea)/Ra的变化;而电枢电流Ia变化使电磁转矩M=CMΦIa随之变化,电磁转矩M变化又影响到转速n的变化。因此机械惯性和电磁惯性的影响是相互联系的。
在第二阶段中,动力学关系由运动方程式决定,即
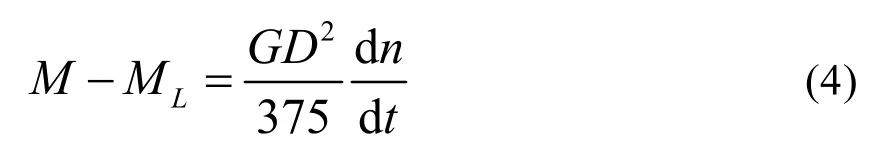
式中:M——电磁转矩;
ML——静负载转矩为常量;
GD2——总飞轮矩为常数。
若忽略由于电枢电流变化引起铁芯中涡流的影响,就可认为电磁转矩是与电枢电流成正比的:

电枢电流决定于动态的电压平衡方程式
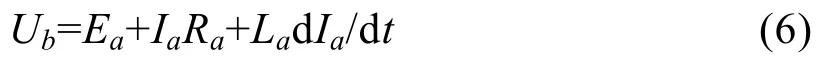
式中Ub、Ra、La都可认为是常量,Ea决定于下式:

根据式(4)、式(6),考虑到上述方程式(5)和式(6)就可得出机械-电气过渡过程的转速方程式和电枢电流方程式。
由式(4),考虑到M=CMΦIa,得
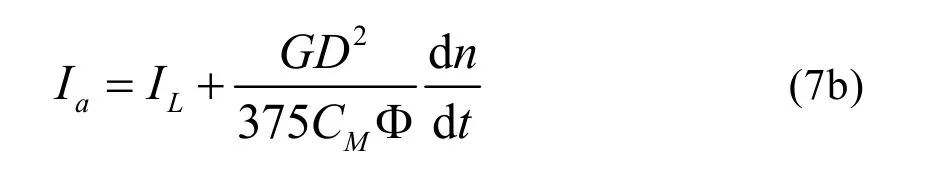
将式(7b)代入式(6)考虑到式(7),经过整理,得转速微分方程式:
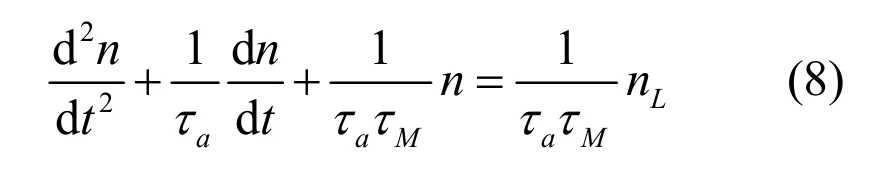
同理得电流微分方程式:
式中:τa=La/Ra——电枢电路的电磁时间常数;

态转速;
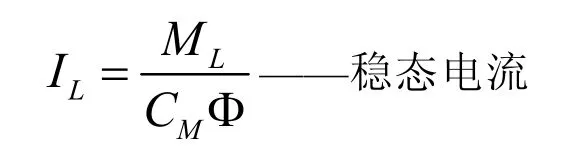
可见式(8)、式(9)都是二阶常系数非齐次线性微分方程式,它们的通解是:
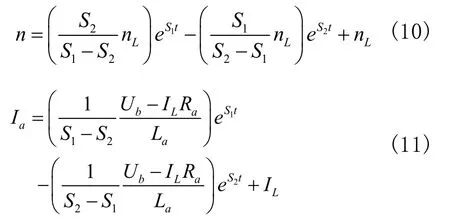
3 电机起动过渡过程仿真
采用matlab软件的Simulink仿真工具对电机起动过程进行仿真【4】,模型如下图2所示。
得到电机起动转速曲线和电枢电流曲线如下 图3、图4所示。
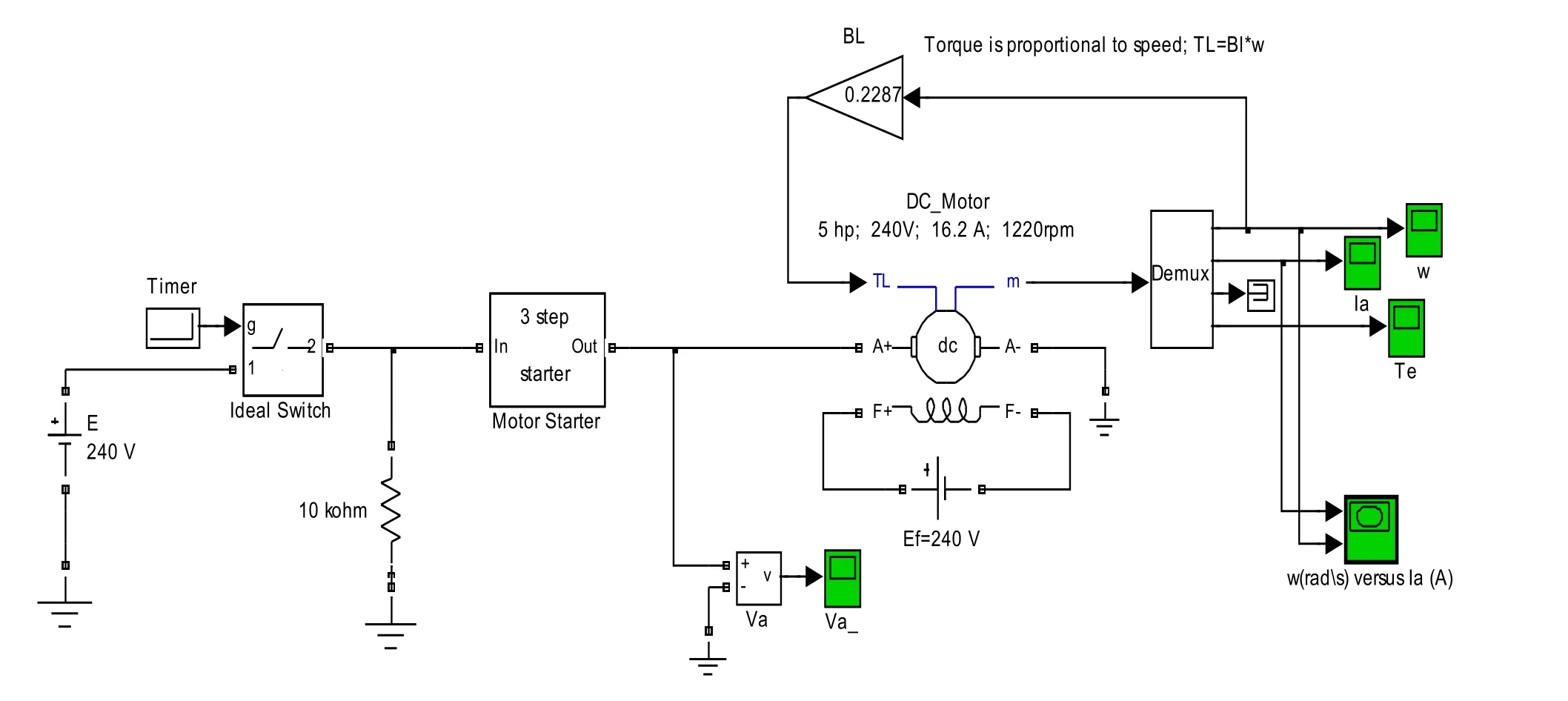
图2 电机起动过程仿真模型
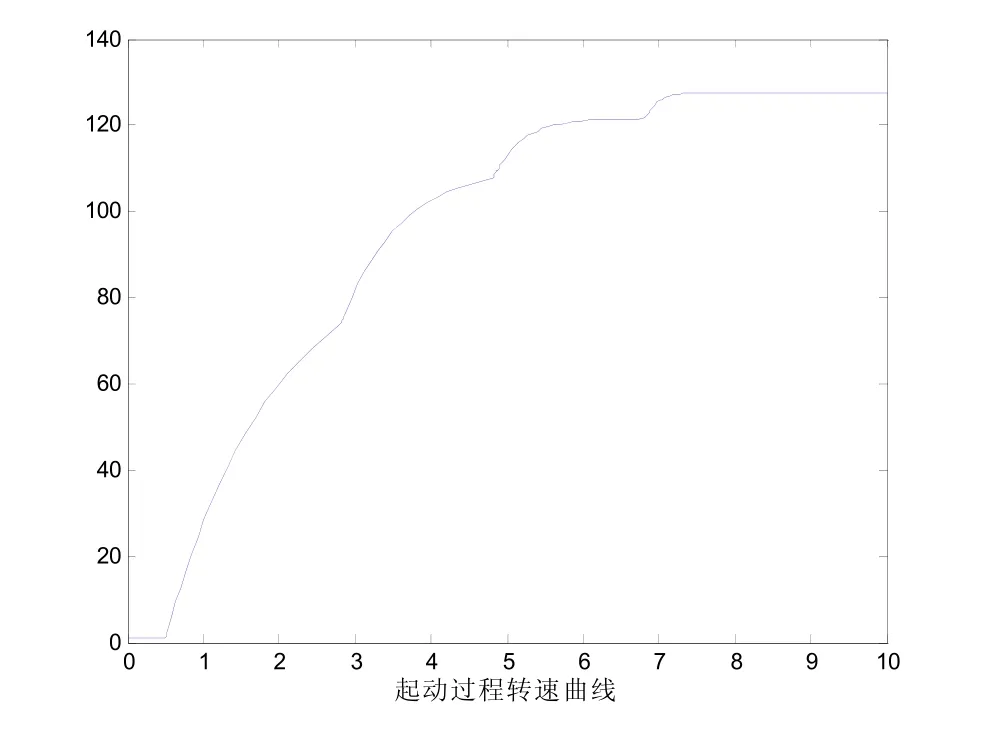
图3 起动过程转速曲线
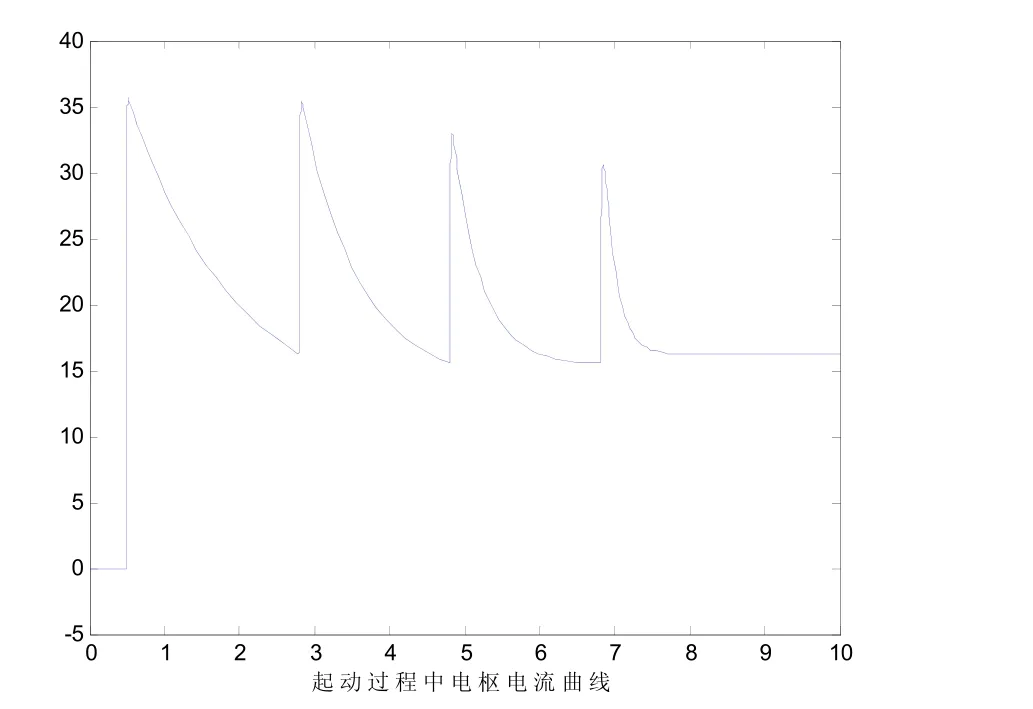
图4 起动过程电枢电流曲线
4 结论
通过解析计算及仿真结果可以得到双转永磁直流电机起动电流以及转速的变化曲线,为电源系统的设计提供了依据。
[1]曾和清. 稀土永磁汽车起动电动机特性分析〔J〕.邵阳高专学报, 1998(1): 20~26.〔4〕.
[2]应崇实. 电机及拖动基础〔M〕. 北京: 机械工业出版社, 1988年11月.
[3]陈家金, 王金平. 船舶电力推进系统的发展. 世界海运, 2006,(4).
[4]张兰. 电力系统动态模拟及其应用综述.湖南工程学院学报, 2004(3).
[5]高景德等. 交流电机及其系统分析. 北京: 清华大学出版社, 2005.

