基于β参数B样条基函数及改进PSO算法的PID神经网络控制

周西峰

（南京邮电大学 自动化学院，南京 210046）

0 引言

在工业控制过程中，由于传统的PID的控制参数难以选择[1]，使其很难适应于对复杂系统的控制，而神经网络凭借其具有的非线性特性、可实现自适应控制等优势被引入到控制领域中，但在实际应用中，其控制效果并不理想，文献[2]对此进行研究并发现其主要原因为：1）是神经网络的仿真训练时间长，不能满足快速性要求；2）是连接权重随机初始化，影响控制结果；3）是神经元函数为静态函数，不适合控制动态系统。基于以上原因，本文采用了B样条函数作为网络隐层神经元函数，主要考虑到B样条网络的知识在网络中是局部存储及学习的，其学习速度较快，文中又提出重新参数化概念，从而建立训练时间短, 动态性能好的B-BP-PID。在学习算法选择方面，文献[3]提出的类似结构的学习算法采用传统BP算法—梯度下降法，但事实上，BP算法全局搜索能力弱，易陷入局部最优，由此，文中选择PSO算法[4]作为B-BP-PID控制器训练算法，在解决实值最优问题方面，PSO可以取得理想效果，但算法在进化后期存在速度变慢以及早熟现象，由此，文中提出由考虑到早熟的改进粒子群算法取代传统BP后向传播算法，从而建立PSO-B-BP-PID控制器，实验仿真证明整个控制过程控制效果良好。

1 β参数型-B样条基函数

B样条函数是工程中常见的一种插值函数，可用于处理几何造型、图像和神经网络等问题，文献[4]即提出由B样条函数作为神经网络隐层活化函数结构，B样条网络神经元函数一般为静态函数，不适合控制动态系统，如果可以找到一种动态调整的B样条基函数，必将促进神经网络更好地应用于PID动态控制系统，由此提出曲线重新参数化概念。

在对曲线重新参数化过程中，可以考虑先对一般B样条函数进行参数变换，再寻找具有更广意义的基函数。下面以三次均匀B样条基函数为例说明这种函数的建立过程。

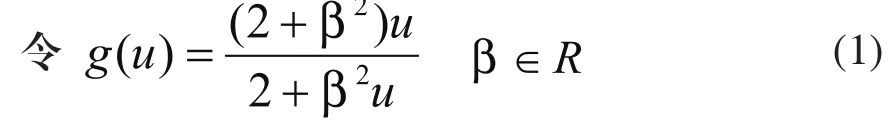
这里将公式（2）称为改进型B样条基函数，记为β参数型-B样条基函数，利用该函数可以将常规的B样条基函数进行推广。分析式（2）可知：当β=0时，可见，β参数型-B样条基函数是常规B样条基函数的推广形式，只要变化参数β，即可实现对曲线的重新参数化。

2 改进的PSO

粒子群优化算法（Particle Swarm Optimization,PSO）[6]是由Kennedy和Eberhart提出的一种优化算法。该算法初始化为一群随机粒子，通过迭代找到最优解。如公式(3)[6]所示。其中表示第i个粒子在k次迭代中的第m维的速度及当前位置, c1,c2为加速系数，r1,r2是介于[0，1]之间的随机数。

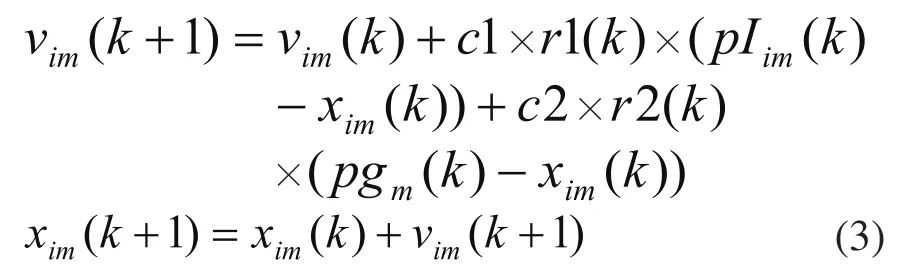
粒子群优化算法的收敛速度快，运算简单，但在进化后期存在速度变慢以及早熟的现象[6],即粒子将逐渐靠近局部最优点，此时，粒子间距离必然可以反映其聚集程度，因此本文即利用距离来判断粒子是否发生早熟“聚集”，并按照式(4)定义一个距离方差：

其中，DJ，DAVG分别为第J个粒子到目前局部最优粒子的距离以及粒子群中各粒子到该局部最优粒子的平均距离，D为归一化因子，其取值可采用公式：反映了粒子聚集程度。在未达到全局收敛条件且

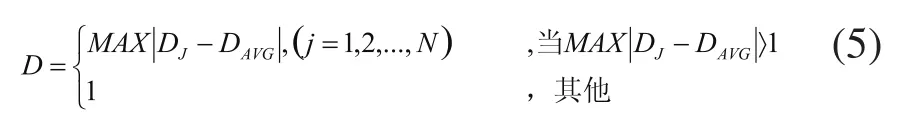
早熟发生时，考虑让假性最优粒子跳出局部最优位置，即对局部最优粒子速度加干扰项，然后再调整其位置值，具体调整算法如(6)式：

其中，a=4，fim为0 -1间随机数，vimax和vimin分别为第i个粒子迄今为止最大和最小速度，b为当前早熟粒子飞离局部最优的强度控制，根据局部聚集的程度可以选择该参数为大于0的整数。通过以上调节公式，粒子将在新位置以新速度开始搜索，从而跳出原早熟区域。

3 PSO-B-BP-PID控制器的完整控制过程

首先介绍一下PSO-B-BP的基本结构，由输入层、隐含层和输出层组成。输入层有3个神经元，输入信号分别为系统输入rin，输出yout，输入与输出间误差error；隐层采用三次均匀β参数型-B样条基函数；输出层采用sigmoid函数，具体网络结构如图1示。

图1 PSO-B-BP网络结构

在调整过程中，由改进粒子群算法对神经网络权值wi，wo以及B样条函数控制参数β进行更新，具体控制过程如下:

1）初始化神经网络权值wo，wi，节点个数NIN=3，NYIN=4，NOUT=3，初始化控制器输出值为0，初始化粒子群算法的各个参数。

2）根据控制对象的传递函数,由当前输入rin(k)计算输出yout(k)，并计算误差函数error(k)=rin(k)-yout(k)，从而得到神经网络输入信号xi=[rin(k),yout(k),error(k)]。

3）将输入信号xi送PSO-B-BP的输入层，由计算输入神经元的输出Oin。

4）对Oin进行规一化预处理后将送入到隐层计算，其中，三次均匀的β参数型-B样条的4个基函数分别作为隐层4节点函数。

5）将隐层输出Oyin(i)送入输出层，输出层采用sigmoid函数。

6）计算PID控制器输出u(k)，并根据实际情况对其限幅。

8）根据3式粒子群算法位置和速度公式来更新每一个粒子的当前速度和位置。

9）计算评价每个粒子适应度，更新个体极值pbwo，pbwi，pbβ和全局的极值gbwo，gbwi，pbβ。

10）进行早熟判断及相关处理。

11）K=K+1，误差不满足且K＜K1，转步骤8），否则，寻优结束，并得到输入权值wi，输出权值wo，参数β的全局最优值gbwo，gbwi，pbβ。

12）将gbwo，gbwi，pbβ再送给PSO-B-BP的输入层，按照3）-5）步来计算最优Oout(i)。

13）重复步骤6），得最优输出u(k)，最后，由控制对象传递函数关系，计算最优控制输出值yout(k)。

4 仿真

被控制系统方程定义如（7）式所示：

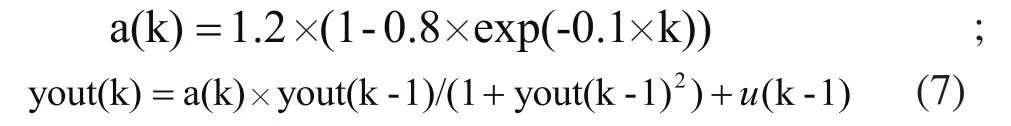
网络节点个数分别为NIN=3，NYIN=4，NOUT=3，控制器输出初始值u(k)=0；加速系数c1=c2=2.05；惯性因子ω=0.9；粒子数m=10；迭代次数k1=10；系统输入信号采样数为600，采样间隔ts=0.01。实验中分别对PSO-B-BP-PID(采用改进的PSO及β参数型-B样条基函数),B-BP-PID(采用传统B样条及BP算法)，PSO-BP-PID(采用传统PSO及sigmoid函数)的控制效果进行MATLAB仿真。

在此输入下，3种控制器仿真结果如图2-图4所示：

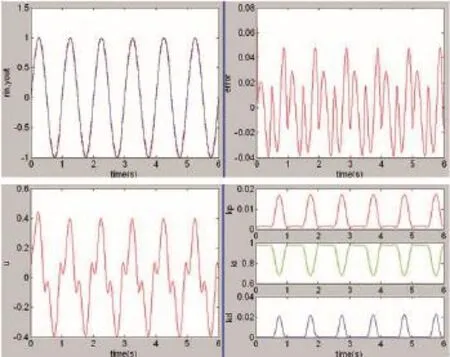
图2 PSO-B-BP-PID控制器的仿真输出

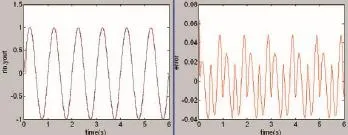
图3 PSO-BP-PID控制器的仿真输出

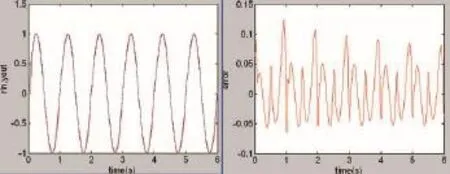
图4 B-BP-PID控制器的仿真输出

比较各算法跟踪曲线变化过程可知，BP-PID控制器单纯与PSO或B样条相结合的控制效果都不如与两者共同结合的效果好，这主要是因为B样条函数具有局部正支撑性，单位分割性和最小支撑性等优点，由B样条函数构成的神经网络具有较好的联想能力和全局搜索能力；在学习算法方面由于采用了考虑到早熟问题的基于群体智能原理的粒子群优化算法，可以避免传统意义的BP算法陷入局部最优解的缺点，且简单易行。除此以外，B样条网络的知识在网络中是局部存储的，学习也是在局部进行，因此，具有较快的学习速度，这样也可以抵消PSO的在寻优迭代过程的时间消耗。

除以上原因外，本文算法的两个改进过程的优点也在仿真中有所体现。一方面，B样条函数采用了可以重新参数化基函数，通过PSO搜索，能找到最佳适合β因子,从而控制得到适合本网络权值搜索的最佳B样条函数（文中最后搜索的β=3）;另一方面，对学习算法的PSO增加了早熟的判断和处理，可以有效克服传统PSO易于陷入局部最优的缺点，从而提高神经网络模型的预测精度。

5 结论

本文采用可重新参数化B样条神经网络设计B-BP-PSO控制器，并改进粒子群算法取代传统BP后向传播算法，从而建立PSO-B-BP-PID控制器。该控制器结合了可以通过搜索得到最佳适合 因子，从而控制获得适合本网络权值搜索的最佳的重新参数化的B样条基函数以及可以有效克服传统PSO易陷入局部最优缺点的改进PSO学习算法的优点，因此可以提高控制过程的稳定性、精确性与鲁棒性。仿真结果表明基于PSO-B-BP-PID的控制系统可以实现对被控系统的良好控制。另外，文中PSO搜索过程只用10步，粒子数只有10个，若适当增加步数及粒子数，其控制效果将更佳。

[1] FARDADI M,SELK GHAFARI A,HANNANI S K.PID neural network control of SUT building energy management system[C]//Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics.New York:IEEE Press,2005:682– 686.

[2] SHU H L,SHU H.Simulation study of PID neural network temperature control system in plastic injecting-moulding machine[C]//Proceedings of the 6th International Conference on Machine Learning and Cybernetics.New York:IEEE Press,2007:492 – 497.

[3] 景小宁,李全通,南建国.B样条神经网络的算法设计及应用[J].计算机应用与软件,2005,22(7):93-96.

[4] KENNEDY J,EBERHART R C,Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.New York:IEEE Press,1995:1942 – 1948.

[5] Xianming chen,Richard F.Riesenfeld.An Algorithm for direct multiplication of B-Splines,IEEE TRANSACTIONS ON AUTOMATION SCIENCE AND ENGINEERING,2009,6(3):433-442.

[6] Shi Y,Eberhart R C.A modifi ed Particle Swarm Optimizer[C].Ieee International Conference on Evolutionary Computation,1998:69-73.