线性状态等式约束下两种 H∞滤波的比较
王兆敏, 徐 杰, 何腊梅, 刘 瑜
(四川大学数学学院,四川成都610064)
1 引言
工业中,含有线性状态约束的控制使用越来越广泛,然而在处理实际问题中,对于含有线性状态约束的随机模型或者随机信号,一般采取忽略或启发式思考的方法[1]。实际上,某些已知的信号或许不该被忽略。为此,在投影系统和无约束的 H∞滤波方程的基础上,考虑线性状态等式约束的条件,给出了一种含线性状态等式约束的H∞滤波。通过比较其与状态投影下的 H∞滤波的一步向前估计误差协方差的上界,得出了文中所给方法的估计性能优于状态投影下的H∞滤波的估计性能的结论。并给出一个数值模拟的例子,验证了上述结论。
对含有状态约束的H∞控制及其状态估计,已经进行了较多研究[2-4]。在文献[5-7]理论基础上,对传统的带有加性白噪声的随机系统模型,如果状态变量满足硬的等式约束(所谓的硬的等式约束,就是状态变量之间的关系确切知道),伴随着加在其上的约束,过程噪声的协方差是奇异的[7]。为了设计正确的满足状态等式约束的H∞滤波,必须用到实际(奇异)的带有约束的噪声协方差矩阵。文中,把基于投影系统含有状态约束的H∞滤波称之为投影系统约束的H∞滤波。主要关注投影系统约束的H∞滤波的推导及其与状态投影H∞滤波的状态估计性能比较。所谓状态投影H∞滤波,就是把无约束的H∞滤波投影到状态约束的平面上。在文献[5]中,D Simon证明了无约束的H∞滤波估计误差协方差的上界不高于状态投影的 H∞滤波估计误差协方差的上界的结论。将给出状态投影的H∞滤波估计误差协方差的上界不高于投影系统约束的 H∞滤波估计误差协方差上界的证明。
注:为记法简便,文中把基于投影系统带线性状态约束的H∞滤波的状态估计称之为投影系统约束的H∞滤波的状态估计。把无约束的H∞滤波投影到约束的状态平面上的估计,称之为状态投影的H∞滤波估计。对于矩阵 A,AT为A的转置。对于对称矩阵P,P>0或者P<0表示P是一个正定的或者半正定的矩阵。
2 带有等式约束的线性系统
假设线性系统的动态模型为:

状态约束条件为Dkx=0。其中,Dk是已知s×n阶约束矩阵,0是 s维零向量,s为约束个数,n是状态变量个数,且s≤n。假定Dk是行满秩的,即Rank(Dk)=s。这个条件较容易满足,因为若Dk不满足满秩的条件,则可通过去掉其相关行使其满秩,去掉多余的状态约束条件即可。并且可以正规化,即DkD=I。其中状态变量 xk∈Rn。把矩阵Dk的左零空间记为这里代表观测向量。均是零均值的白噪声。并且有
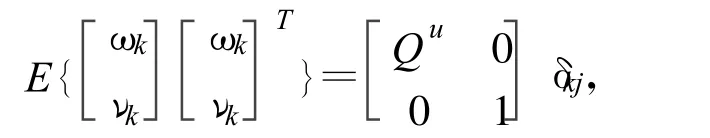
3 随机系统下含线性状态约束的H∞滤波
首先给出不含线性状态等式约束的H∞滤波的方程,然后给出状态投影和投影系统约束下的H∞滤波的方程。状态投影的 H∞滤波就是把无约束的状态估计投影到状态约束的平面上,而投影系统约束的H∞滤波则是通过正确的使用过程噪声协方差矩阵来得到。继而,通过比较投影系统约束的 H∞滤波和估计投影H∞滤波的估计误差协方差的上界,可以看出投影系统约束的 H∞滤波的估计性能更优一些。
3.1 不含线性状态等式约束的H∞滤波
对于线性系统(1),通过文献[6]知,将假定对手的输入如下其中是一个确定的增益,是一个给定的矩阵,可以称为可调参数或者加权矩阵为一个噪声序列。假定和是不相关的白噪声序列,并且它们均与不相关。矩阵可由对手噪声输入的先验信息来调整。+1表示在观测{,,…,}下状态+1的估计。状态估计表达式为其中为状态估计的增益,从文献[6]中知:

3.2 状态投影的H∞滤波
对于满足线性等式约束的随机系统(1),在文献[5]中,通过把无约束的状态估计ˆxk投影到约束平面上,给出了状态投影的H∞滤波方程。文中,把它叫做状态投影的H∞滤波,用上标(◦)p来表示。状态投影的 H∞滤波解决如下问题:

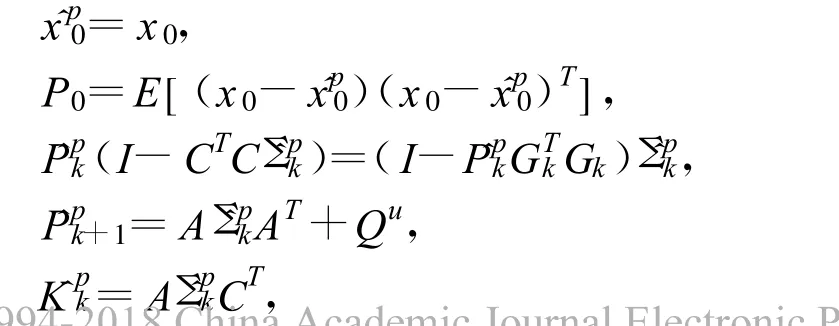

3.3 投影系统约束的H∞滤波
在这一节中,为了记号的简单,用D来代替Dk。在文献[7]中,由于D是行满秩的,所以DT的列向量线性无关,因此可以定义DT的左零空间。记DT的左零空间的正交补空间为D⊥,并且满足DT⊥DT=0和DT⊥D⊥=I。因此,存在唯一的序列zk∈R(n-s)满足

由zk的定义及系统(1),可知

将式(5)代入式(4)中,可以得到:

其中PN(D)≜D⊥DT⊥表示零空间D的正交投影。而根据文献[8],可知如果选择 PN(D)=P(Qu)-1=I-QuD(DTQuD)-1DT,会得到更好的结果。约束的H∞滤波在系统投影下的表达式如下:

其中Qc=P(Qu)-1QuP(Qu)-1,上式成立的条件为并且有
定理:对于式(3)中所给状态投影的一步向前估计误差协方差的上界,和式(7)中给出的投影系统约束的估计误差协方差的上界,投影系统约束的估计误差协方差的上界不大于状态投影的估计误差协方差的上界,即
证明:假定当前时刻两个状态估计相同,也就是 ˆxp=ˆxc,于是有以及于是由从式(2)和式(3)可得
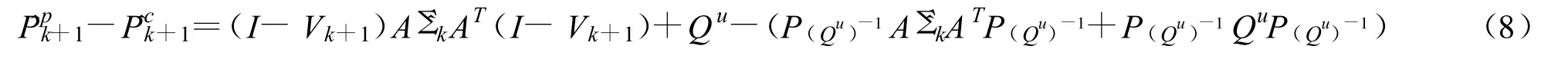
所以
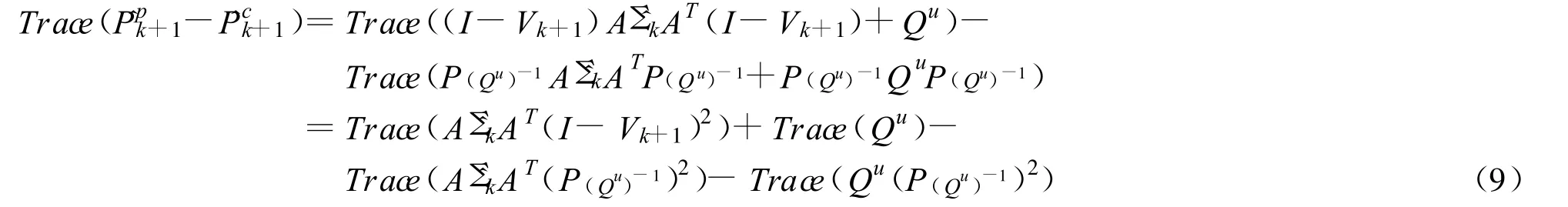
又因为
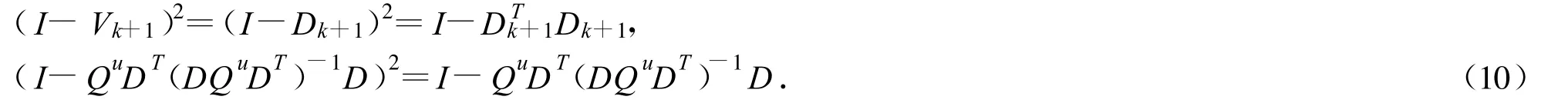
所以

又(I-Vk+1)和(I-QuDT(DQuDT)-1D)的每个特征值为0或者1,而且 Qu是非奇异的,所以有 Trace(Aˆ∑kAT.从文献[8]中,可知

由式(10)可知,(I-Vk+1)2=I-Vk+1,故 Trace((I-Vk+1)Qu(I-Vk+1))=Trace(Qu(I-Vk+1)).
又因为(I-Vk+1)的每个特征值为0或者1,根据文献[9],可得

由于式(12)中不等号两旁的矩阵为正定矩阵,结合式(13)则有

4 数值模拟
考虑如下例子,对于一个用GPS导航系统定位的陆地车辆,其运动轨迹可由下面的系统模型来逼近[8]:

首先标准化观测方程,使得观测噪声的协方差为单位阵,然后给出正规化的观测yk如下:

在数值模拟中,给出如下形式的过程噪声和观测噪声:

并且假定车辆沿方位角α在一条直路上行驶,于是约束方程给出如下:

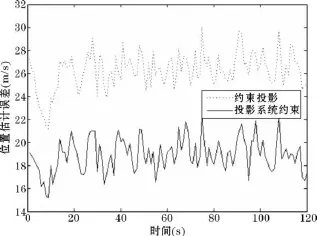
图1 H∞滤波位置估计误差曲线对比曲线

图2 H∞滤波速度估计误差曲线对比曲线
图1和图2中的位置和速度估计误差指的是估计误差的均方根误差(RMS)。从图上可以看出投影系统约束的H∞滤波的估计性能要优于约束投影 H∞滤波的估计性能。
5 结论
比较了两种带有线性状态等式约束的H∞滤波的状态估计性能,并证明了约束投影H∞滤波误差协方差的上界不大于投影系统约束的H∞滤波误差协方差的上界。数值模拟验证了文中的结论。当然关于约束状态的H∞滤波还有问题去研究,比如投影系统约束的H∞滤波的稳定性问题等。
[1]Massicotte D,Morawski R,BarwiczA.Incorporation of a positivity constraint into a Kalman-filter-based algorithm for correction of spectrometric data[J].IEEE transactions on Instrumentation and Measurement,1995,44(1):2-7.
[2]Sideris A,Rotstein H.Constrained H∞optimal control over an infinite horizon[J].SIAM Journal of control and Optimization,1997,35(4):1244-1262.
[3]Neto A,Castelan E,Fischman A.H∞output feedback control with state constraints,in control of Uncertain systems with Bounded Inputs[M].New York:Springer-Verlag,1997:119-127.
[4]Alamir M,Balloul I.Robust constrained control algorithm for general batch processes[J].International Journal of control,1999,72(14):1271-1287.
[5]Simon D.A game theory approach to constrained minmax state estimation[J].IEEE Transactions on Signal Processing,2006,54(2):405-412.
[6]Simon D.Optimal State Estimation[M].New York :John Wiley&Sons,2006:381-389.
[7]Sangho.Ko,Robert R.Bitmead.State estimation for linear systems with state equality constraints[J].IEEE Transactions on Automatic Control,2007,43:1363-1368.
[8]Chen Tianshi.Comments on “State estimation for linear systems with state equality constraints”[J].IEEE Transactions on Automatic Control,2010,46:1929-1932.
[9]Horn R,Johnson C.Matrix Analysis[M].Cambridge:Cambridge University Press,1990:22.

