π/4-DQPSK调制系统的差分解调信息容量近似分析与计算

李明华, 白宝明

(西安电子科技大学综合业务网国家重点实验室,陕西西安710071)

1 引言

π/4-DQPSK是一种基于QPSK的线性窄带数字调制技术,由美国贝尔实验室的P A Bake于1962年提出。π/4-DQPSK相对于DQPSK,最大转移相位从π减少到3π/4,引起的包络浮动较小,适于非线性传输信道。同时,π/4-DQPSK调制具有频谱特性好、频谱利用率高、抗多普勒频移等优点,被广泛的研究和应用,如美国的个人接入通信系统(PACS)和IS-136数字蜂窝系统、日本的个人数字蜂窝系统(PDC)、欧洲数字集群标准(TETRA)和中国的数字集群移动通信系统体制国家电子行业标准A都采用了此调制技术。

传统的π/4-DQPSK调制信号的解调方法包括相干解调和差分解调。相干解调方法需要有信道的显式或隐式估计,这要求依次发送导频或训练信号[1],并且要求接收机和载波同步,不易实现。差分解调不需要接收机和载波同步,可以克服相位模糊,但与相干解调相比有性能损失。1990年,D Divsalar和M K Simon提出多符号差分检测[2],检测性能随同时检测的符号长度N的增加而改善,但这种检测方法复杂度很高。1994年,K M Machenthun,Jr提出一种快速的多符号差分检测算法[3],降低了多符号检测的复杂度,使得多符号检测方法可以被实际应用。另一方面,文献[4]提出在非冗余纠错(Nonredundant Error Correction,NEC)检测算法[5]基础上利用Viterbi算法[6]改善π/4-DQPSK解调译码性能,但其改善的性能距相干检测仍有距离。文献[7]提出衰落信道上的差分分组解调算法。

根据π/4-DQPSK信号的两符号差分解调(非相干检测)原理,对AWGN信道上π/4-DQPSK调制差分解调系统的信息容量进行了分析[8-11],并且采用熵估计的数值方法获得了系统的可达信息速率,给出了π/4-DQPSK差分检测的容量曲线图。从容量分析的数值结果可以看出,π/4-DQPSK差分检测存在门限效应,当信噪比低于该门限值时,系统谱效率的降低不会使系统性能提高。目前,关于差分检测系统的容量限的讨论还较少,文献[12]论述了正交FSK调制非相干检测系统的容量,文献[13-15]讨论了非相干AWGN信道的容量,文献[16]从容量限的角度分析了不同差分编码调制方案的性能。

2 系统模型

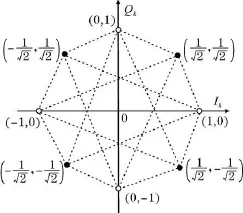
图1 π/4-DQPSK信号星座图

π/4-DQPSK调制将输入的两个比特映射成复值调制信号,其信号星座如图1所示。

图1中的星座图中有8个信号点,包括4个白点指示的信号点和4个黑点指示的信号点。星座点间的连线代表码元转换时刻相位的跳变,每次相位只能在白色信号点和黑色信号点之间交替变换,避免了QPSK中的180°相位变化。由图1可以看出,相位跳变量有±π/4和±3π/4这 4种取值。

采用π/4-DQPSK调制信号的编码通信系统框图如图2所示,假定接收机采用非相干信号检测技术,对接收到的输入信号进行差分解调。

图2 π/4-DQPSK调制解调框图[8]

先简单介绍差分编码调制的方法。有两种方法可以实现差分调制：对输入数据先进行差分编码,再映射到π/4-QPSK信号的绝对相位上;或者直接映射输入数据到相对相位上。假定采用Gray映射编码,根据图2和输入数据与相位偏移量的关系可知,k时刻的相位差(信息相位)如表1所示。

表1 输入数据与相位偏移量的关系表

由表1,可以得到对应于k时刻输入数据的信息符号vk=ejΔθk,经过差分编码之后,第k时刻的发送信号为：

其中Es是每发送符号的平均能量,θk代表k时刻发送信号的绝对相位,Δθk代表k时刻输入数据所表示的相位差。令xk=xI,k+jxQ,k,则有：

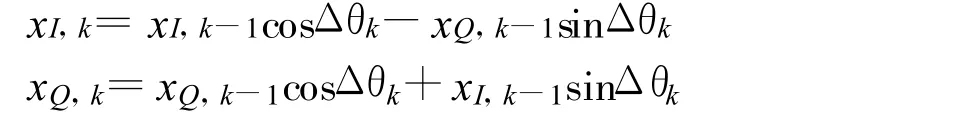
在采用非相干解调的情况下,接收信号与发送信号之间可能存在载波相位误差,接收机接收的等效复基带信号可表示为：

其中hk为信道衰落系数,在AWGN信道中,hk=1;nk～CN(0,N0)是均值为零,每维方差为σ2=N0/2的圆对称复高斯噪声变量。φ为载波相位估计误差。假定φ在两个相邻符号周期上保持不变,则两个接收符号上的相位差独立于φ。在采用两符号差分检测的情况下,检测器的输出为

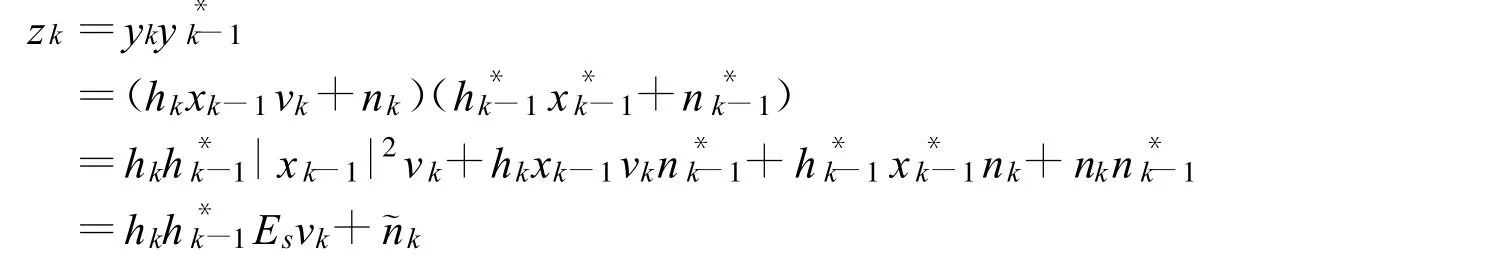
3 离散输入连续输出信道的容量计算

在式(3)中 ,输入 vk=ejΔθk是一个离散随机变量 ,其取值范围为 V={ejπ/4,ej3π/4,ej5π/4,ej7π/4};输出 zk∈ C 是一个复连续随机变量。根据信息理论,该信道的信息容量的计算公式为[9]：

2012年镇江市积极采取措施进行智慧城市建设并取得一定成效［2］。2016年在《镇江市“十三五“规划纲要》中，镇江市人民政府明确提出要推进“智慧镇江”建设，全面提升一体化基础设施建设水平。2018年镇江市荣获“2018中欧绿色智慧城市奖”。目前镇江智慧城市建设已经进入发展新阶段。扬中市智慧城市建设一方面能够为镇江下属县级市例如丹阳、句容、丹徒等提供建设样本，以点带面整体推进镇江全市范围内的智慧建设；另一方面，扬中市加强与镇江产业合作创新，对传统产业进行升级转型，促进经济共享、资源共享、共同发展，为镇江经济社会发展贡献力量，进一步推动“智慧镇江”建设。

其中P(v)为输入 V的概率函数(pmf)。假设信道输入信号是等概的,即P(v)=1/|ν|,∀v∈ν,此时C退化为计算可达信息速率：

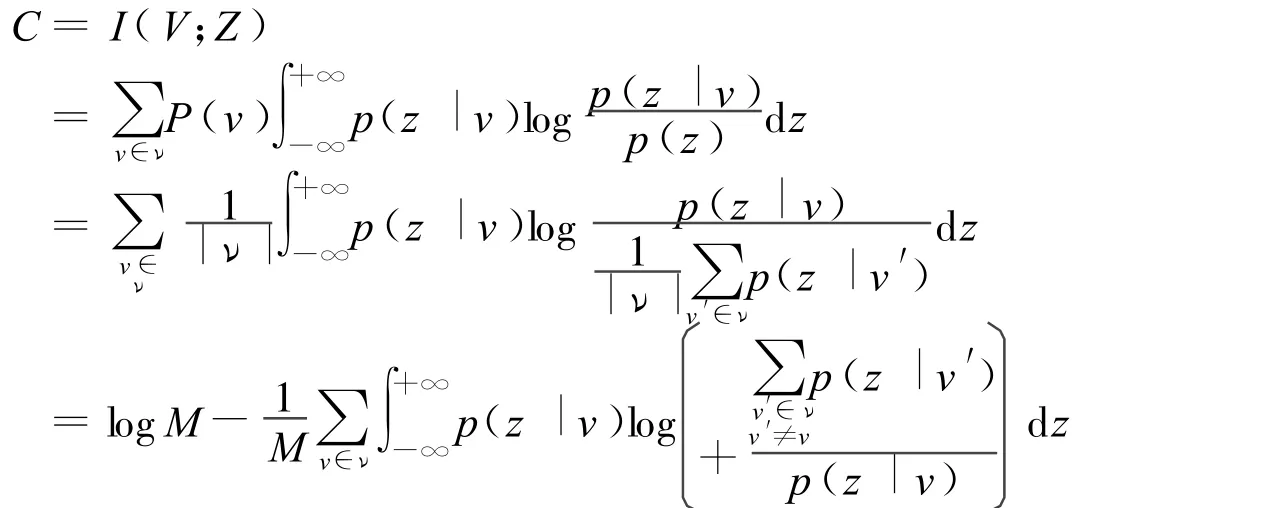
其中M=|ν|。由于p(z|v)是非高斯的,没有一般的解析表达式,所以一般教科书中针对AWGN信道的互信息计算公式在这里不能直接应用。采用如下方法来进行数值计算：

首先将连续变量z离散化,将涉及概率密度函数(pdf)p(z|v)的计算转化为的计算,这里 ¯z=q(z)为 z的量化值,q(◦)表示量化函数;

其次,采用基于Monte Carlo的数值方法,求出 pmf P(¯z|v);

然后,采用熵估计方法,根据式(5)计算互信息。

4 基于熵估计的互信息数值计算方法

熵估计是指根据一组有限的观察序列X=[x1,x2,…,xN]可以估计出连续随机变量X的概率密度函数,从而得到X的熵值。熵估计的方法有多种,如基于模型(Model Based Method)的估计方法、贝叶斯估计法以及柱状图(Histogram Method)估计法[10]。由于柱状图估计法实现简单、算法复杂度低,文中选用该方法进行熵估计。

输入v的取值有4种,分别用xA,xB,xC,xD来表示。为了得到信道转移概率假定对每一种v的取值进行N次概率实验,即在输入的条件下,独立产生 N个AWGN变量nk,经过信道传输与差分解调之后得到 N个检测器输出zk=(zk,I,zk,Q)。根据熵估计的计算原理可以求出zI序列和zQ序列的区间范围,即[],然后将该区间划分为L个子区间,即z的量化级数为L。由此可以确定出的值。类似地,可以分别求出和

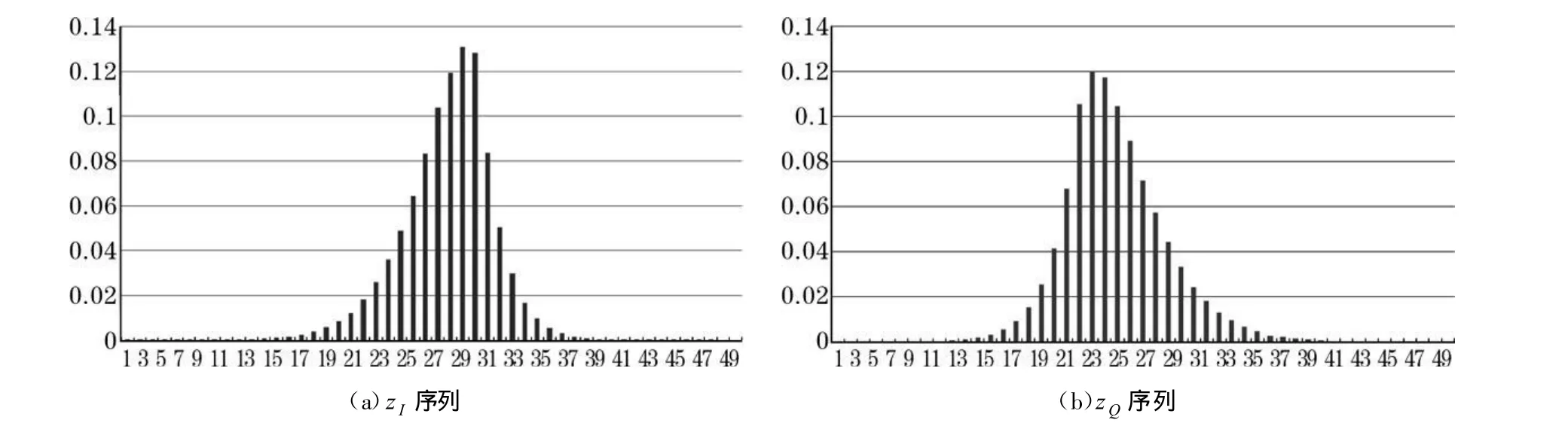
图3 输出序列量化后的柱状图

5 数值结果及分析

基于前面的理论,对每一个给定的信噪比,通过C++编程数值计算P(¯z|v)并应用式(6)即可获得相应的容量曲线。对所有信噪比下的信道输出采用相同的区间划分,均取 L=50个子区间;随机实验次数N=1.5×105。所得的π/4-DQPSK差分检测的容量曲线结果如图4所示。

图4 π/4-DQPSK差分检测的容量曲线图

观察横坐标分别为Es/N0和Eb/N0时容量曲线的变化,可以看出在容量大于0.35bits/symbol时,两条曲线都是容量随着横坐标dB值的增加而增加,图4(a)中容量是到13dB左右达到饱和,而图4(b)中容量是到10.5dB左右达到饱和,两者都是饱和于2bits/symbol。而当容量小于0.35bits/symbol左右的时候,两条曲线有了明显的区别：在图4(a)中容量依然是随着dB值的增加而增加,而在图4(b)中容量是随着dB值的增加反而减小。这是由于 Es/N0和Eb/N0的换算原理,即公式[9]

当信噪比低于C=0.35bits/symbol所对应的Es/N0值时,系统容量会随着Es/N0的减小而急剧下降(如图4(a)所示),致使Eb/N0反而增加。这是差分解调带来的不足,文献[11]的正交调制非相干检测系统的容量曲线也体现了这个特点。

与此同时,相比于以往的相干检测容量曲线图,Eb/N0都是随着码率也就是这里的谱效率(容量值)的减小而减小;在相同的误码率的情况下,谱效率越低,所要求的dB值越小。但从图4(a)可以看出0.35bits/symbol以下的曲线是随着码率减小,所要求的dB值反而越大,也就是说差分检测(非相干检测)在0.35bits/symbol左右时达到最佳工作点。

综上所述,从图4可以观察到下列两个结果：

(1)差分解调的门限效应：当信噪比低于C=0.35bits/symbol所对应的Es/N0值时,系统性能(容量)会随着Es/N0的减小而急剧下降,则该为门限值。由图4(b)知 C=0.35bits/symbol所对应的 Eb/N0约为3.1dB,从而由式(7)可以确定出π/4-DQPSK差分检测的门限值为 Es/N0=C◦Eb/N0=0.35×100.31,即-1.459dB。这样就从信道容量的角度解释了差分检测的门限效应,并给出了门限值。

(2)在信噪比低于该门限值时,即使采用低码率的信道码,降低系统谱效率,也不会带来所需Eb/N0减小,即系统性能的提高。

6 结束语

主要讨论了π/4-DQPSK差分检测的信息容量问题,基于差分检测原理和熵估计的数值计算方法得出了近似容量曲线图并对其进行了对比分析及讨论。由此,得出以下结论：

差分解调存在门限效应,当信噪比低于C=0.35bits/symbol所对应的Es/N0值(称为门限值)时,系统性能(容量)会随着Es/N0的减小而急剧下降;并且在信噪比低于该门限值时,即使采用低码率的信道码,降低系统谱效率,也不会带来所需Eb/N0的减小,即系统性能的提高。

[1]X Wang,H V Poor.Wireless Communication System：Advanced Techniques for Signal Reception[M].Englewood Cliffs,NJ,USA：Prentice-Hall,2004.

[2]D Divsalar,M K Simon.Multiple-symbol differential detection of MPSK[J].IEEE Trans.Communications,1990,38(3).

[3]K M Mackenthun.A fast algorithm for multiple-symbol differential detection of MPSK[J].IEEE Trans.Communications,1994,42(2).

[4]郭道省,张邦宁,杨喜根,等.一种新的π/4-DQPSK解调译码方案[J].信号处理,2001,17(3).

[5]S Samejima,K Enomoto,Y Watanabe.Differential PSK system with nonredundant error correction[J].IEEE T rans.Selected Areas in Communications,1983,1(1)：74-81.

[6]Hui-Ling Lou.Implementing the Viterbi algorithm[J].IEEE Signal Processing Magazine,1995：42-52.

[7]D M Zook,C W Baum.An iterative differential block demodulation algorithm for fading channel[J].in Proc.MILCOM 2002,2002,(10).

[8]宋文妹,张天骐,林孝康.π/4-DQPSK调制解调技术的仿真及分析[J].计算机仿真,2006,(8).

[9]白宝明.现代数字通信与编码理论讲义[M].西安：西安电子科技大学,2007.

[10]J F Bercher,C Vignat.Estimating the entropy of a signal with applications[J].IEEE Trans.Signal Processing,2000,48(6)：1678-1694.

[11]A Guillén i Fàbregas,A Grant.Capacity approaching codes for non-coherent orthogonal Modulation[J].IEEE Trans.Wireless Communications,2007,6(11)：4004-4013.

[12]W E Stark.Capacity and cutoff rate of noncoherent FSK with nonselective Rician fading[J].IEEE Trans.Commun.,1985,33(11)：1153-1159.

[13]R Nuriyev,A Anastasopoulos.Capacity and coding for the block-independent noncoherent AWGN channel[J].IEEE Trans.Inform.Theory,2005,51(3)：866-883.

[14]G Olavolper,I C Ahel.The capacity of the concoherent channel[J].Europ.Trans.Telecomm.,2001,12(4).

[15]M Katz,S Shamai(Shitz).On the capacity-achieving distribution of the discrete-time noncoherent and partially coherent AWGN channels[J].IEEE Trans.Inform.Theory,2004,50(10).

[16]R F H Fischer,L H J Lampe,S H Müller-Weinfurtner.Coded modulation for differential encoding and noncoherent reception on fading channels[J].ITG,2000.