CRLS算法在智能天线中的应用
赵翠芹, 申东娅, 段艳明, 易云飞, 包玉珍
(1.河池学院计算机与信息科学系,广西宜州546300;2.云南大学信息学院,云南昆明650091;3.云南科技信息职业学院,云南昆明650224)
1 引言
智能天线(Smart Antenna)通常也称作自适应天线阵列(Adaptive Antenna Array),是在自适应滤波和阵列信号处理的基础上发展起来的,利用多天线系统组成的天线阵列进行数字信号处理来完成信号的空间滤波和定位。自适应天线阵列在无线通信系统中的一个关键问题是在视距(Line of sight,LOS)和非视距(Non line of sight,NLOS)情况下的性能差异。在视距情况下,通过对天线阵列适当加权后产生一个天线方向图,其主波束跟踪用户信号的波达方向(Direction of Arrival,DOA)),旁瓣或零对准干扰信号到达方向,达到充分利用移动用户信号并抑制干扰信号,从而达到增强期望信号并抑制干扰信号,提高通信容量和质量的目的。该技术被广泛应用于波形分集MIMO(Multiple Input Multiple Output)通信[1]、声纳和MIMO雷达[2-3]等系统中。随着大规模、超大规模集成电路和数字信号处理技术的迅速发展,数字波束形成技术逐渐在移动通信领域中受到人们的关注3G标准TD一SCDMA采用的关键技术是以波束形成技术为核心的智能天线技术[4]。
目前,有几种流行的优化智能天线算法[5-10],包括最小均方(Least Squares Minimization,LMS)算法[7-8]、采样矩阵求逆(Sample Matrix Inversion,SMI)算法、递归最小二乘算法(Recursive Least Squares,RLS)、恒模算法(Constant Modulus Algorithm,CMA)、共轭梯度算法、波形互异算法[9]和基于遗传算法的赋形波束算法[10-11]。在这些算法中,LMS算法是在时域采样以确定最优权值样点,如果时域信道变化复杂,则权值更新也变得很复杂。为了克服这个问题,块自适应方法,比如采样矩阵求逆SMI算法被提出。虽然SMI算法收敛快,但相关矩阵条件差导致错误或求逆时变成奇异矩阵。此外,大型天线阵面临求逆的挑战。RLS算法的优势在于不需要对大量相关矩阵求逆,递归的方程使相关矩阵求逆更容易更新。这些算法都是无约束的优化算法。
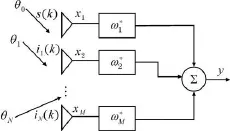
图1 窄带自适应阵列系统
2 算法分析
窄带M 元自适应阵列系统结构[5]如图1所示,期望信号从 θ0角到达,干扰源从 θ1,…,θN角到达。含 M个权值的M个阵元天线接收期望信号和干扰源。阵元每个接收信号还包括加性高斯噪声。时刻用第k次采样表示。因此,加权后的天线阵输出y可表示为:

其中(◦)H表示共轭转置;表示天线阵权值,(◦)T表示转置表示期望信号向量;xi(k)表示干扰信号向量,n(k)表示每个信道的零均值高斯白噪声;ai表示M个阵元的天线阵在到达方向θi上的导向向量。信号d(k)是参考信号,与期望信号s(k)相同,与干扰信号in(k)不相关。设代价函数为阵列的期望输出功率:

其中Rxx为输入信号x的自相关矩阵。根据自适应波束形成算法,当维持可视方向为单位响应时,算法权值可以通过最小化输出功率来计算:

窄带波束限制条件为[9]:

采用拉格朗日数乘法来解决最优权值,通过非确定的拉格朗日乘数λ将限制条件和代价函数结合:

求式( 5)的梯度,并令梯度为零,即可求得式( 5)的最小值,即最优权值

将( 6)式带入( 4)式可求出拉格朗日乘数:

式(7)带入式(6),可得

通过时间平均可估计相关矩阵,得

其中 l是观察周期。由于使用长度为l的数据块,因此这种方法称为块自适应,一块一块地调整权值。按以下步骤,用matlab很容易计算天线阵相关矩阵。定义矩阵Xl(i)为l次数据快拍范围内x个向量的第i个块。于是
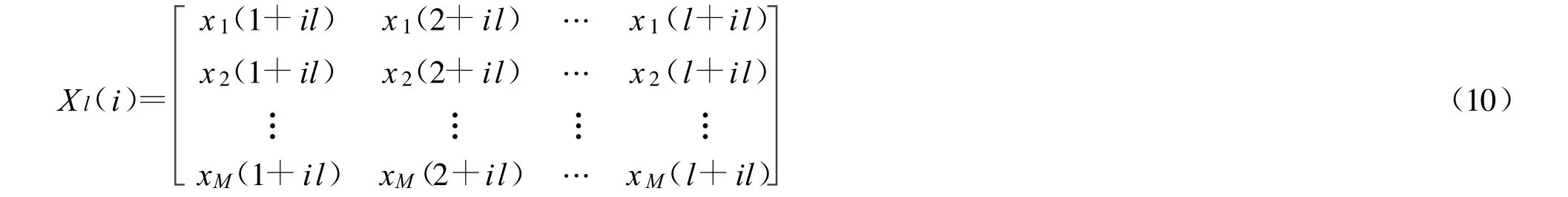
其中i是块号,l是块长。为了方便计算,省略l而将相关矩阵重新写为:

其中l是块长,最后一次采样为 l,Rxx(l)是终止于采样时刻 l的相关估计。式(11)求和是使用矩形窗口,因此考虑前面所有的时间采样。由于信源可变或随时间缓慢移动,所以可以不关注最早的数据采样,而只关注最近的数据采样。修改(11)式,以便去掉最早的时间采样。这种称为加权估计。因而有

其中α是遗忘因子。遗忘因子有时也称指数加权因子。α为正数,即0≤α≤1。当 α=1时,就是常见的最小二乘算法,且表明记忆无限。将式(12)的求和分为两项,即前i=l-1项值的求和以及最后一项i=l的值。

使用前面的值可以求得后面的天线阵相关估计。借助Sherman Morrison-Woodbury(SMW)定理[13]求R-1xx(l)。SMW定理为

将式(14)运用到式(13)中,得如下递推公式:
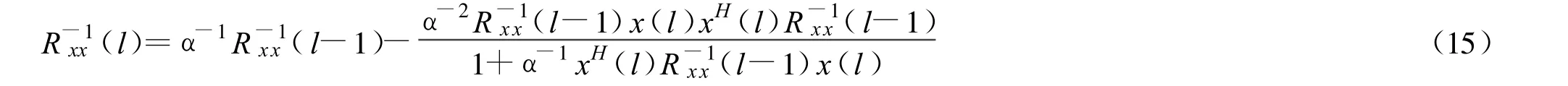
(15)式称为递归最小二乘算法的Riccati方程。将(15)式代入(8)式,即可求得最优权值。
3 几何解释
CRLS算法有一个简单的几何解释,这个解释对算法的可视化纠错性能非常有用。式(5)是天线阵权值的二次函数,性能曲面J(ω)呈椭圆形的抛物面形状,有一个最小值。图2为J(ω)的等高线图,从图2可以理解强加约束的过程。对二维系统,恒功率平面aHω=1平行于通过原点的aHω=0的平面。平面aHω=1与等高线相切,由原点指向切点的矢量即为最优权值向量ωopt,ωopt是最小化闭环表达式描述的最优约束权值向量。
4 算法仿真及性能分析
用matlab对CRLS算法进行仿真。假设阵元模式为均匀线性阵列,接收信号的到达角 θ0=30°,干扰信号到达角为 θI=-60°,期望接收信号向量为xs(i)=a0s(i),其中 s(l)=cos(2πt(l)/T),且 T=1ms。采样次数 l=50,t=(0:l-1)*T/(l-1)。干扰信号向量是 xI(l)=aIi(l),i(l)=sin(πt(l)/T)。天线阵的初始权值 ω(1)=0。遗忘因子α=0.89。图3仿真了极坐标系下阵元间距d=0.5λ,λ为波长,天线数目为变量的方向图;图3(a)阵元数目 M=8;图3(b)阵元数目 M=12;图4仿真了直角坐标系下阵元间距 d=0.5λ,天线数目为变量的方向图,图4(a)阵元数目 M=8;图4(b)阵元数目 M=12;从图 3和图4可以看出CRLS算法具有较好的稳定性;图5仿真了阵元数为10,阵元间距 d为变量的方向图,图5(a)中 d取0.5λ,有相同大小的主瓣;图5(b)中d取0.65λ,属于低采样情况,在观察方向上有相同的结构(波束宽度),也注意到波束模式中有附加的波峰,波束模式中这些附加的瓣称为栅瓣。栅瓣产生空间模糊性;即从栅瓣对应的方向传播到阵列的信号,看起来像是从有用方向来的信号。波束形成器无法区分各个方向上来的信号,为了避免空间重叠,阵元间隔必修是d≤0.5λ。图6给出了用估计的最优权值计算出来的输出信号和期望信号的比较图,从图6可以看出算法有较强的跟踪能力。
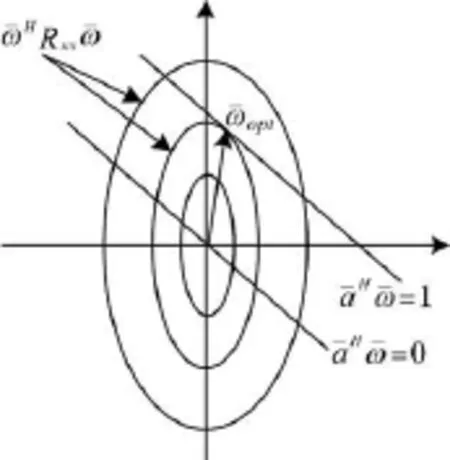
图2 约束权值矢量以便最小化输出功率的功率等高线几何描述
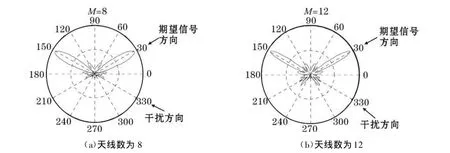
图3 在极坐标系下的阵列因子图

图4 在直角坐标系下的阵列因子比较图

图5 天线数为10的阵元间距不同的方向图
5 结束语
作为MIMO关键技术之一的智能天线能在发射机或接收机快速移动时,通信系统中的许多用户可以占用同一个信道工作而互不干扰,以一个或多个高增益的窄波束分别对准并跟踪所需信号的方向,同时以波束零点对准并跟踪干扰信号的方向,这就实现了所谓的“空分多址(Space Division Multiple Access,SDMA)”。
首先详细推导了CRLS算法,在这一算法中,协方差的畸变响应被最小化。其次,对约束条件给出了几何解释。最后用matlab进行了仿真,给出了不同天线数目和不同阵元间距的方向图、期望信号和采用CRLS算法的输出信号的比较图,并对仿真结果进行了详细的分析和比较。仿真结果表明,CRLS算法不仅有较好的稳定性,而且算法也有较强的跟踪能力,算法得到的波束性能较好,在干扰方向形成零陷,具有较好的抗多址性能。
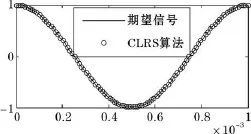
图6 期望信号的获取与跟踪的比较图
致谢:河池学院青年课题立项项目(2011A-N008)对本文的资助
[1]Lita J,T Kwok-Yeung Lo.Digital Beamforming in Wireless Communications,Artech House[M].Boston:MA,1996.
[2]Fishler E,A Haimovich,R Blum,et al.MIMO Radar:An Idea Whose Time HasCome[C].Proccedings of the IEEE Radar Conference,2004(26/29):71-78.
[3]Rabideau D,P Parker.Ubiquitous MIMO Multifunction Digital Array Radar,IEEE Signals,Systems,and Computers[C].37thAsilomar Conference,2003,1:1057-1064.
[4]Liberti J,T Rapport.Smart Antennas for Wireless Communications:IS-95 and Third Generation CDMA Application[M].New York:Prentice Hall,1999.
[5]张贤达,保铮.通信信号处理[M].北京:国防工业出版社,2000.
[6]金荣洪,耿军平,范瑜.无线通信中的智能天线[M].北京:北京邮电大学出版社,2005.
[7]何亚军,桂良吕,李霞.智能天线:MATLAB版[M].北京:电子工业出版社,2009.
[8]王兵.基于智能天线的LMS算法的研究[J].计算机与现代化,2011,4(14):14-16.
[9]Gross F B.Smart antennas for wireless communications with MATLAB[M].[S.l.]:McGraw-Hill,2005.
[10]O L Frost.An algorithm for linearly constrained adaptive array processing[J].IEEE Proc.,1972,60(8)926-935.
[11]武琳静,李京华,王景,等.基于遗传算法的智能天线波束形成[J].现代电子技术,2010,21(5).
[12]赵福玲,王永军,何绍林,等.遗传算法综合智能天线的赋形波束[J].电波科学学报,2011,26(3):593-597.
[13]Golub,G H,C H Van Loan.Matrix Computations[M].The Johns Hopkins University Press,1996.

