悬置刚度对动力总成悬置系统解耦率的影响分析

李 楠，简晓春，张 超，周志伟

(1.重庆交通大学 交通运输学院，重庆400074;2.重庆铁马工业集团有限公司，重庆400050;3.比亚迪股份有限公司，广东深圳518118)

减少发动机振动向乘客的传递是提高NVH性能的重要手段［1］，良好的动力总成悬置系统是提高车辆NVH性能的前提之一［2］。已有较多的研究通过对悬置系统的优化来降低振动的传递［3］。但是目前仍存在很多尚待探索的领域［4］。

动力总成悬置系统主振动方向的能量解耦率直接影响到系统的匹配性能。它受悬置安装位置、悬置的阻尼和刚度等多因素影响［5］。如果系统中有严重的耦合振动，如何快速在众多的影响因素中进行选择及合理调试，成为工程师们面临的难题。笔者以常见的3点式动力总成悬置系统为研究对象，用主振动方向的能量解耦率作为评价指标，先用正交试验的方法，结合人们面对问题时，先进行部分分析，然后进行综合分析的层次规律［6］，分别针对悬置系统的3个悬置元件，设计3个正交试验。然后用极差分析法对试验仿真结果进行分析，并找出对系统各主振动方向解耦率影响最重要的因素。

1 正交试验

影响系统匹配性能的因素较多，需借助试验设计的方法来了解指标与因素和各因素之间的作用关系。正交试验设计是利用正交表安排与分析的多因素试验方法。其高效性在于它可以用较少的试验次数来反映较全面的情况［7］，并可用相应的极差分析方法、方差分析方法等对试验结果进行分析。

2 试验指标

一般以能量解耦率、力和位移传递率、振动传递率、车厢的振动响应最小等作为动力总成悬置系统的性能评价指标［8］。而目前在动力总成悬置系统匹配分析，仿真和优化中最为常用的是系统主振动方向的能量解耦率。

耦合现象会导致沿悬置系统广义坐标的任一激励都将激起系统的多个模态的振动，难以单独对某一模态进行优化而不影响其它自由度方向的性能，各个模态方向的振动相互影响而不利于整个系统的隔振［9］。因此对动力总成悬置系统进行振动耦合分析已被广泛用于它的设计和优化中［10］。

当悬置系统做第i阶主振动时，其最大动能为:

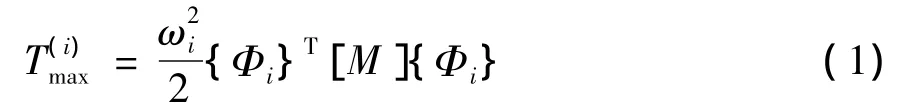
式中:ωi(i=1，2，…，6)为系统的第 i阶固有频率;{Φi}为第i阶固有振型向量。将上式展开为:

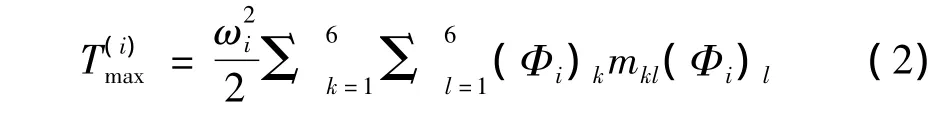
对于6自由度的动力总成悬置系统，系统的全部动能分配在这6个广义坐标上。在第k个广义坐标上分配到的动能为:

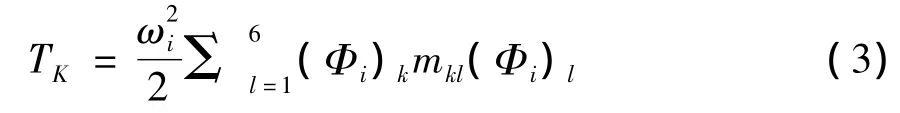
当系统做第i阶主振动时，在第k个广义坐标上的能量百分比为:

通过计算Pki值，可求出系统以第i阶固有频率振动时，在第k个广义坐标方向所占有的能量百分比。如Pki=100%，表示系统做第i阶模态振动时的能量全部集中在第k个广义坐标上，此时系统实现了完全解耦而最有利于振动的控制。

动力总成悬置系统的解耦率有6个，将多指标通过加权转化为单指标。加权评分值Ji的计算公式为:

式中:Ji为第i次试验时系统响应的综合指标。

垂直方向的解耦率最重要，所以相应的权重值应较大。取加权系数分别为:W1=0.133 3;W2=0.133 3;W3=0.333;W4=0.133 3;W5=0.133 3;W6=0.133 3。

3 因素水平表

3.1 动力总成悬置系统参数

悬置的坐标系各个主轴刚度方向与悬置系统的定坐标系坐标轴方向一致，坐标原点在悬置的中心位置。其坐标系如图1，G0-xyz是定坐标系，原点在动力总成静平衡时的质心位置;x轴平行于曲轴指向发动机前端;y轴平行于车架上平面并指向汽车左侧;z轴由右手定则确定。所研究的动力总成悬置系统参数如表1。

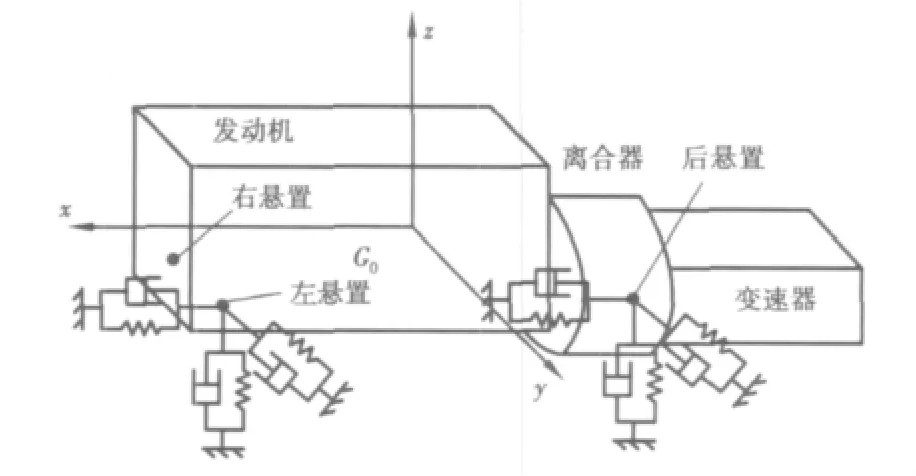
图1 动力总成悬置系统模型Fig.1 Model of powertrain mounting system

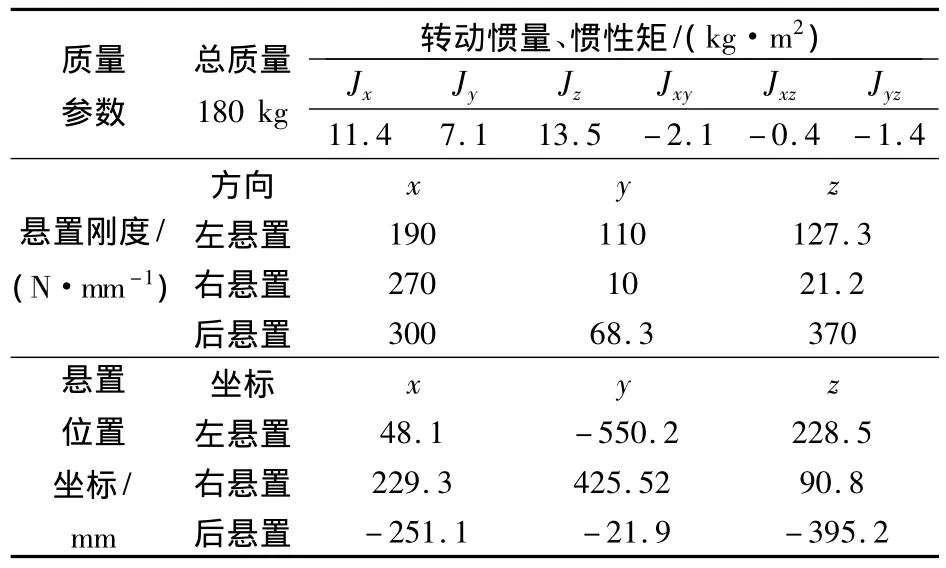
表1 动力总成悬置系统参数Tab.1 Parameters of powertrain mounting system

3.2 因素水平表分析

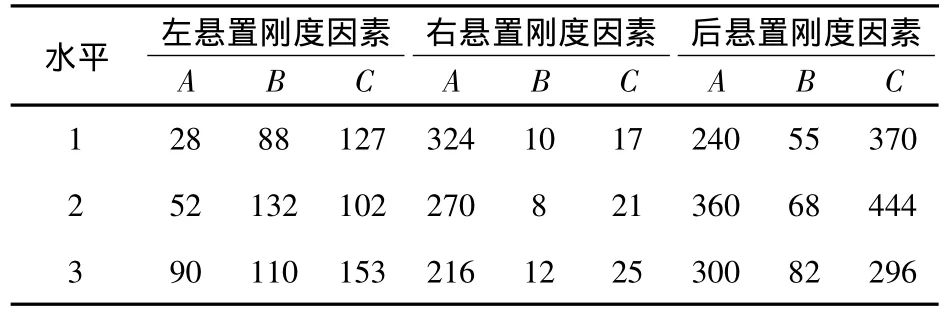
表2 左、右、后悬置的因素水平Tab.2 Level of the factors of the left，right and back mount

取悬置刚度因素的水平数为3，3个水平分别为悬置系统最优化的刚度参数及其上下偏差的20%。分别列出3个悬置各主轴方向的刚度水平如表2，其中，A、B、C 因素分别表示悬置的 x、y、z向的刚度。并将各水平进行随机化排序。

4 正交表选择与表头设计

根据因素数量和水平数目来选择正交表。结合试验工作量的大小，选用L9(34)做正交试验表，选好正交表后，把各因素放在正交表头各列上，见表3。表中的每一行表示试验操作的条件，9行表示要进行9次试验，例如:

第1号试验，A1B1C1——表示前悬置的各向刚度分别取值228，88，127.3 N/mm 时候，对悬置系统的解耦率进行计算。

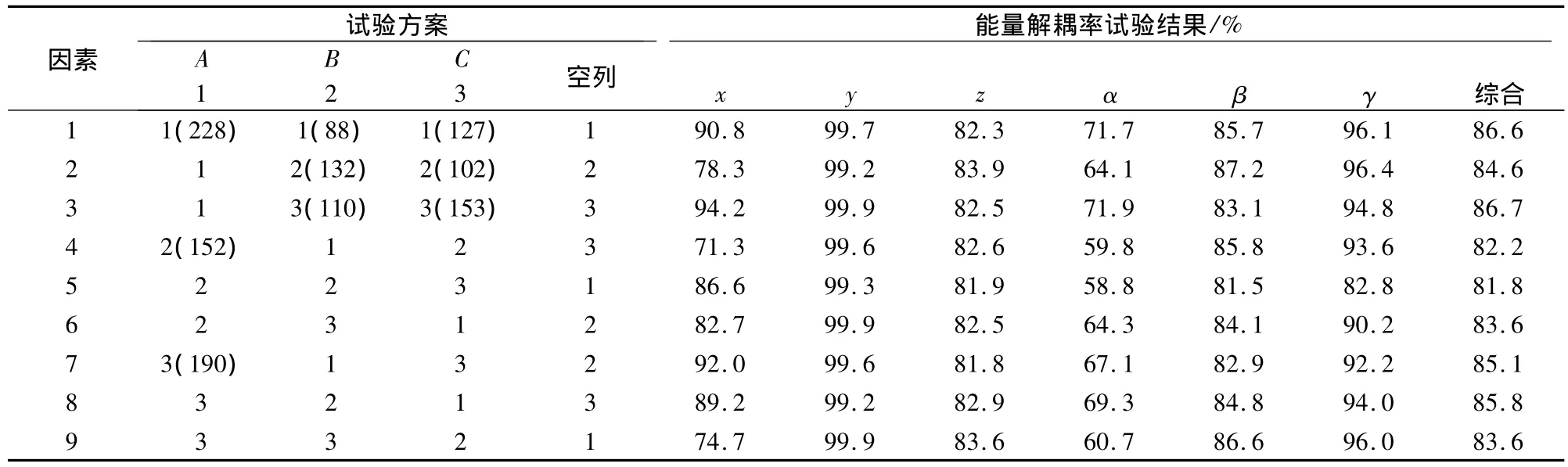
表3 左悬置试验方案及结果Tab.3 Test scheme and result of left mount

5 仿真试验和结果分析

严格按照表3，编制MATLAB系统能量分布仿真试验程序，求出在不同因素水平组合下的系统解耦率，并将结果填入该表中。然后根据试验结果，分别求出各列下的和 T，R 为K1，中最大数减去最小数之差——极差，T为所有试验结果之和。将试验和计算的结果填入表3中。第4列为空列，不放置因素。在进行极差分析中，有时空列的极差比其他所有因素的极差还大，这说明因素间交互作用较明显。

5.1 直接分析

从表3中可以看出，第3号试验，即A1，B3，C3的试验结果最好，综合评分为86.7%，是这9次试验中最好的。

5.2 计算分析

通过对正交试验数据的简单计算，能找出最佳条件，也能求出各个因素影响的重要程度。在表4中，每一列下面列出了该因子各水平试验结果之和K1，K2，K3，平均值和极差R，极差越大的因子对指标的影响越大，反之，影响越小。用因素水平做横坐标，指标值作为纵坐标，画出因素与综合指标的关系趋势图，如图2。

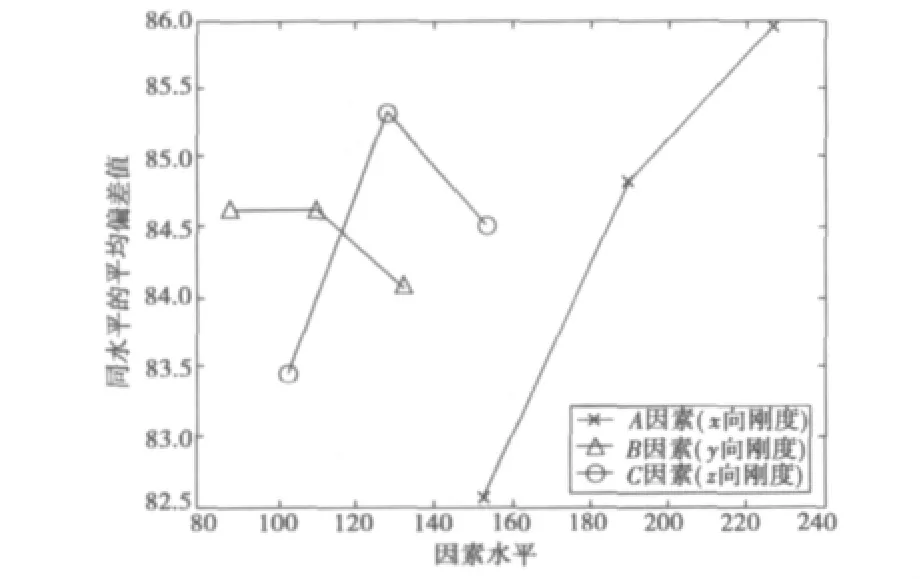
图2 右悬置刚度因素与综合指标的关系Fig.2 Relationship between left mount factors and the synthetical index

为了解悬置的各向刚度对单向指标(x、y、z、α、β、γ方向能量解耦率)的影响，按类似于综合评分的方法，结合表3，分别得出左悬置在以各主振动方向解耦率为指标时的极差，见表5。

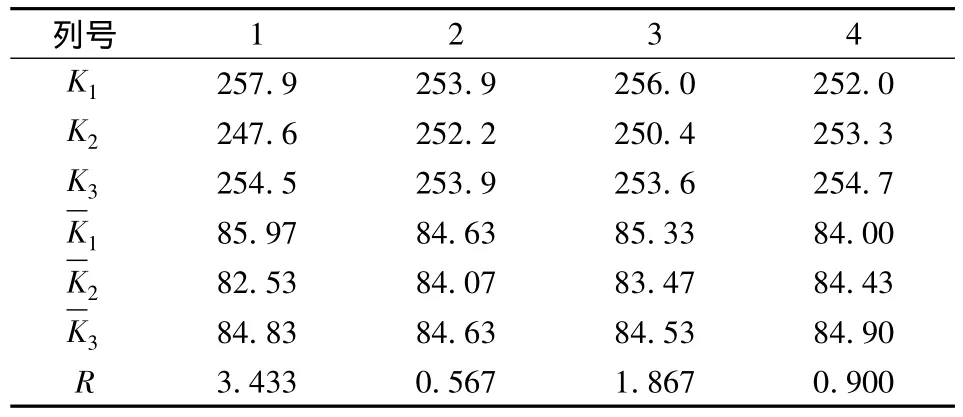
表4 各列极差Tab.4 Extreme difference of each row

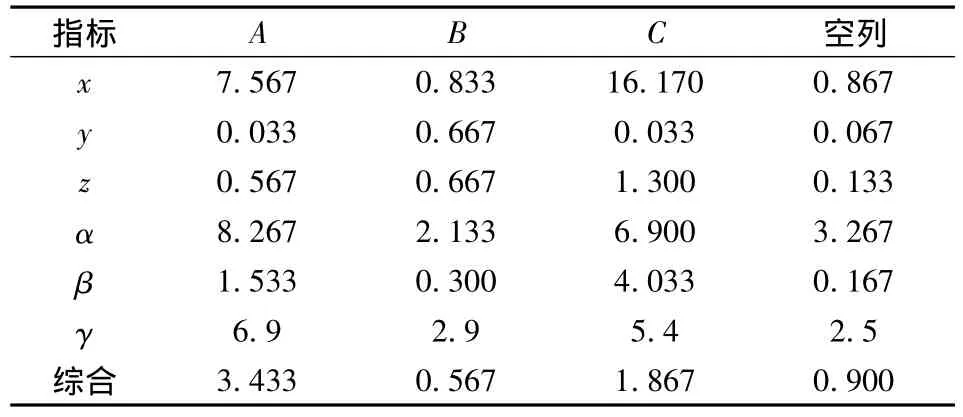
表5 左悬置极差Tab.5 Extreme difference of left mount

由图2和表5，在左悬置的各向刚度中，对悬置系统综合指标影响最明显的因素是A，其次是C和B。对 x，y，z，α，β，γ 方向的解耦率影响最明显的因素分别是 C，B，C，A，C，A，即左悬置的 z，y，z，x，z，x向刚度的影响最为明显。

5.3 右、后悬置的极差

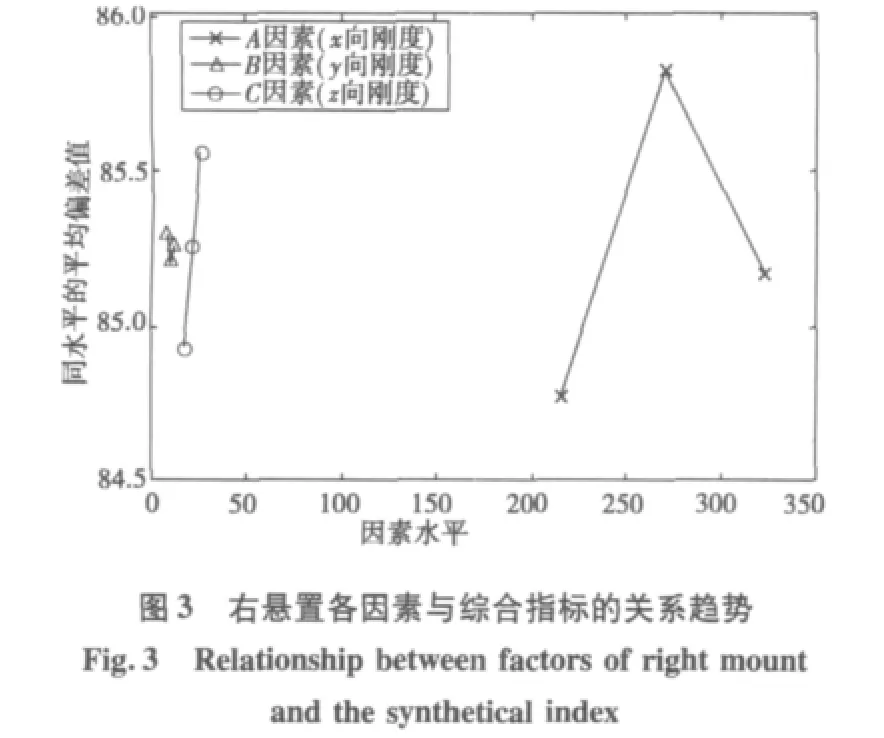
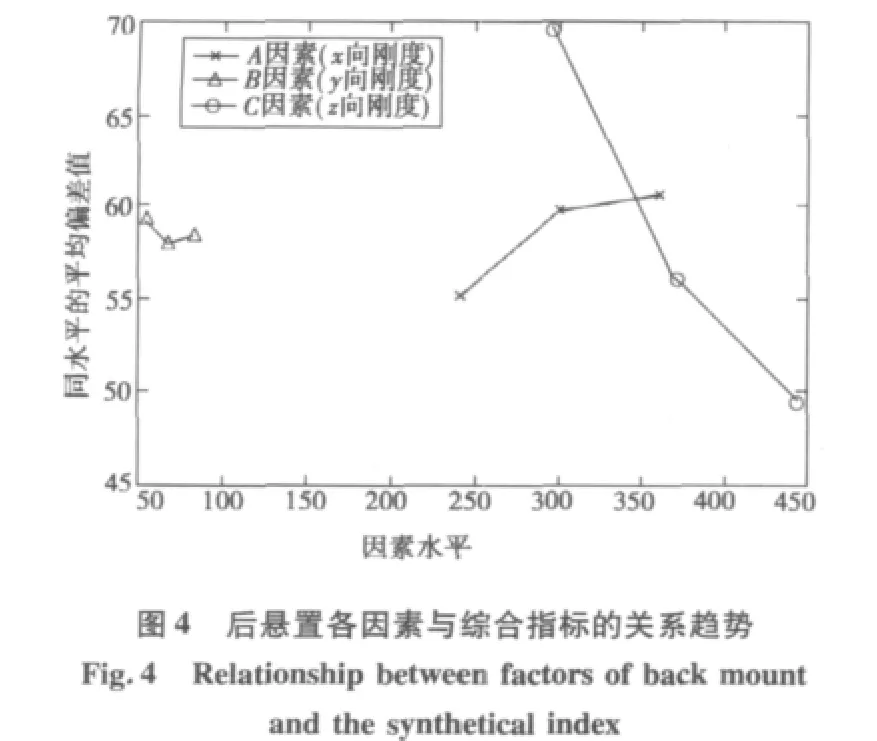
类似于左悬置正交试验的方法，分别对右悬置、后悬置进行试验和极差分析，结果见表6。右悬置、后悬置的因素与综合指标的关系分别如图3和图4。

由表6和图3，在右悬置的各向刚度中，对系统综合指标影响最明显的因素是A，其次是C和B。对x，y，z，α，β，γ 方向的解耦率影响最明显的因素都是A。结合图4，在后悬置的各向刚度中，对悬置系统综合指标影响最明显的因素是C，其次是A和B。对x，y，z，α方向的解耦率影响最明显的因素是C;对β，γ方向的解耦率影响最明显的因素是A。在表6中，右悬置和后悬置在在y方向的极差为0，这是因为在该方向的解耦率已经达到了99.9%以上，计算时由于舍入误差造成的。而对左、右、后悬置，空列的极差没有超过所在行其他因素极差的最大值，这说明，悬置各个主轴方向的刚度的单独作用对系统解耦率的影响更明显。

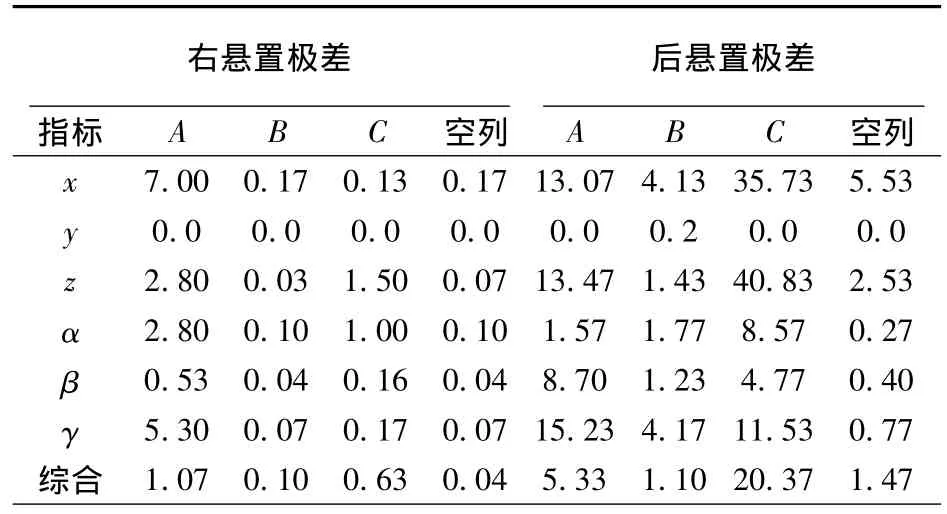
表6 右悬置和后悬置极差Tab.6 Extreme difference of right mount and back mount

6 结论

1)在该动力总成悬置系统的左悬置和右悬置各向刚度中，对系统解耦率影响最明显是它们的x向刚度;而对于后悬置的z向刚度印象最明显。

2)对于该悬置系统的悬置各个主轴方向的刚度的单独作用对系统解耦率的影响更明显。

3)对该悬置系统 x、y、z、α、β、γ 方向的解耦率影响最明显的因素分别为:左悬置的 z、y、z、x、z、x 向刚度;右悬置的x向刚度;后悬置的z向刚度对x、y、z、α方向的解耦率影响最明显，x向刚度对β、γ方向的解耦率影响最明显。

［1］Calv J A，Díaz V，San Román L .Procedure for determining manufacturing defects in a diesel engine in a workshop［J］.Applied Acoustics，2010，71(2):140 －146.

［2］Courteille E，Léotoing L，Mortier F.New analytical method to evalu ate the powerplant and chassis coupling in the improvement vehicle NVH［J］.European Journal of Mechanics:A/Solids，2005，24(6):929－943.

［3］Ali E H，Bruno M，Alexandre L.Vibration reduction on city buses:determination of optimal position of engine mounts［J］.Mechanical Systems and Signal Processing，2010，24(7):2198 －2209.

［4］Lee J H，Singh R.Nonlinear frequency responses of quarter vehicle models with amplitude-sensitive engine mounts［J］.Journal of Sound and Vibration，2008，33(3):784 －805.

［5］吕振华，罗捷.汽车动力总成悬置系统的隔振设计分析方法［J］.中国机械工程，2003，14(3):265 －269.LV Zhen-hua，LUO Jie.Study on vibration isolation analysis of automobile powertrain mount system［J］.China Mechanical Engineering，2003，14(3):265 －269.

［6］梁作民.当代思维哲学［M］.北京:人民出版社，2003:107－108.

［7］秦雯，梁乃兴，陆兆峰，等.湿热地区沥青混合料正交试验分析［J］.重庆交通大学学报:自然科学版，2009，28(5):877－882.QIN Min，LIANG Nai-xing，LU Zhao-feng.Orthogonal experiment analysis on asphalt mixtures at moist hot aea［J］.Journal of Chongqing Jiaotong University:Natural Science，2009，28(5):877－882.

［8］John Brett.Optimization of Engine Mounting Systems to Minimize Vehicle Vibration［C］//Noise＆ Vibration Conference＆ Exposition Technical papers.Detroit:SAE paper，1993:13 －22.

［9］鲍晓东，侯勇.汽车动力总成悬置系统解耦设计研究［J］.西安科技大学学报，2009，27(3):490 －493.BAO Xiao-dong，HOU Yong.Design of automobile decoupling engine mounting system［J］.Journal of Xi’an University of Science and Technology，2009，27(3):490 －493.

［10］孙蓓蓓，李玉麟.汽车发动机悬置系统解耦方法研究［J］.振动工程学报，1994，7(3):240 －245.SUN Pei-pei，LI Yu-lin.Research of automobile decoupling engine bounting system［J］.Journal of Vibration Engineering，1994，7(3):240－245.