PCMA 自适应自干扰对消算法与仿真✴

田文科，王剑，山秀明

（清华大学电子工程系，北京100084）

PCMA 自适应自干扰对消算法与仿真✴

田文科，王剑，山秀明

（清华大学电子工程系，北京100084）

讨论了成对载波多址（PCMA）自适应自干扰对消原理，分析了参数估计误差对自干扰对消的影响。在频偏误差的影响下对消误差为非平稳过程，传统自适应对消滤波器无法收敛。为了克服频偏误差的影响，提出了一种自适应可变遗忘因子（VFF）RLS算法，同时，给出了具有高精度低运算量的模糊函数参数估计算法。仿真证明了VFF-RLS对消算法具有良好的对消性能和稳健性，且需要的额外功率较低，能满足PCMA系统要求。

卫星通信；成对载波多址；自适应干扰对消；VFF-RLS算法

1 引言

成对载波多址（PCMA）技术源自1997年ViaSat公司Mark Dankberg提出的中继通信自干扰对消原理［1］，该技术采用载波叠加的方式，允许通信双方使用相同的频带，能够成倍增加通信容量，节省一倍通信带宽资源，提高通信效率。PCMA这种方式同时还具有较好的安全性，正广泛地应用于卫星通信系统。

PCMA通信双方上行链路采用相同的频带，中继站对同频叠加信号只进行中继转发，不作其它处理。在接收的下行链路信号中需要利用本地信号对消回波信号，得到通信另一方的信号，实现通信。自适应自干扰对消技术是PCMA通信的关键技术。由于回波信号是本地信号经过信道延迟、多普勒频偏漂移、信道衰落等作用的信号，因此自适应自干扰对消算法包括时延、频偏参数估计和自适应干扰对消［2］。

自适应自干扰对消是自适应滤波理论的一个主要应用方向，在最小输出功率约束下，输出信号能达到干扰信号的最小均方估计［3］。PCMA自适应干扰对消利用本地信号对消下行链路的回波信号，采用RLS算法，遗忘因子λ≅1时，可有效进行回波对消。当存在频偏误差时，误差均方值呈非平稳性，标准RLS算法由于遗忘因子是固定值，不能跟踪系统的变化，会发生较大的失调，无法实现干扰对消。遗忘因子是控制RLS算法收敛和误差的关键，对于非平稳环境，产生了多种VFF-RLS算法。通过计算后验误差均方值梯度调整遗忘因子［4］，能较好地适应非平稳变化，但算法比较复杂，对信号比较敏感，在仿真中对频偏干扰的消除并不理想。基于后验误差均方值遗忘因子数值估计算法［5-7］计算简单，但误差较大。文献［8］给出了遗忘因子与先验误差和后验误差均方值的关系，通过估计先验误差和后验误差计算遗忘因子，能较好地跟踪非平稳环境的变化。

本文在文献［8］的基础上，修正了遗忘因子的估计表达式，为PCMA自适应自干扰对消应用提出了一种VFF-RLS算法。同时，给出了应用降采样和sinc函数插值法的模糊函数参数估计算法，该算法在不增加运算量的前提下能有效提高频偏和时延估计精度。最后，通过仿真对本文提出的自适应干扰对消算法进行了验证，并给出了误码率性能曲线。

2 PCMA自适应自干扰对消

如图1所示，接收信号r（t）=s1′（t）+s2′（t）+ n（t），s1（t）是本地基带信号，假设s1（t）、s1′（t）、s2′（t）均值都为零。x（t）为s1（t）附加延迟和频偏估计量的重构信号，＾s1（t）为s1′（t）的估计信号。E（s1（t）s2（t））=0，则有：E（x（t）s2′（t））=0，E（x（t）＾s1（t））≠0。

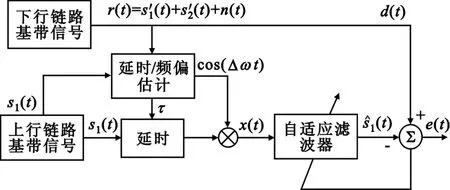
图1 PCMA自适应干扰对消Fig.1 Adaptive interference cancellation for PCMA

由于E{（s2′（t））2}不受自适应滤波器权重系数的影响，使E{e2（t）}最小与最小是等价的，当滤波器收敛到最优系数时，可实现自干扰对消，即e（t）≈s2′（t）+n（t）。对自适应干扰对消滤波器来说，由于rxr=rx（s1′+s2′+n）=rxs1′，最优滤波器的解由x（t）的自相关矩阵和x（t）、s1′（t）的互相关矢量决定。FIR自适应干扰对消滤波器权重系数的最优解为Rxxw=rxr=rxs1′。

定义对消均方误差作为自适应干扰对消的系统误差：

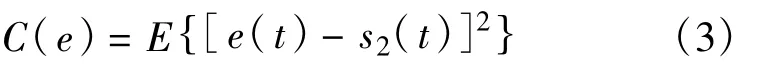
3 频偏和时延误差对干扰对消的影响

假设频偏和时延估计误差为Δf、Δτ，上行回波基带信号s1′（t）=a（k）g（t-Δτ）ej2πΔf（t-Δτ），重构信号x（t）=a（k）g（t），对消误差ε（t）=x（t）-

s1′（t），则均方误差为

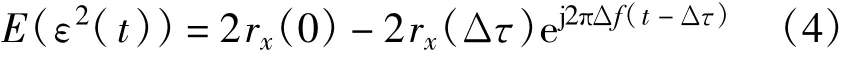
由于时延估计误差相对很小，rx（Δτ）=rx（0），忽略信道衰减影响，则有：

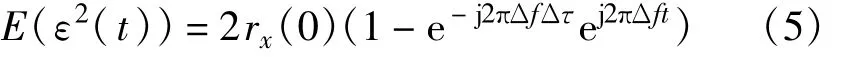
式中，ej2πΔft为时变量，是对自适应干扰对消滤波器的输出产生影响的变化量。即由于频偏误差Δf的影响，对消误差为非平稳过程。在这种情况下，RLS

算法会出现较大误差。图2为标准RLS算法分别在Δf≠0，Δτ≠0，Δf=Δτ=0 3种情况下的对消误差曲线。

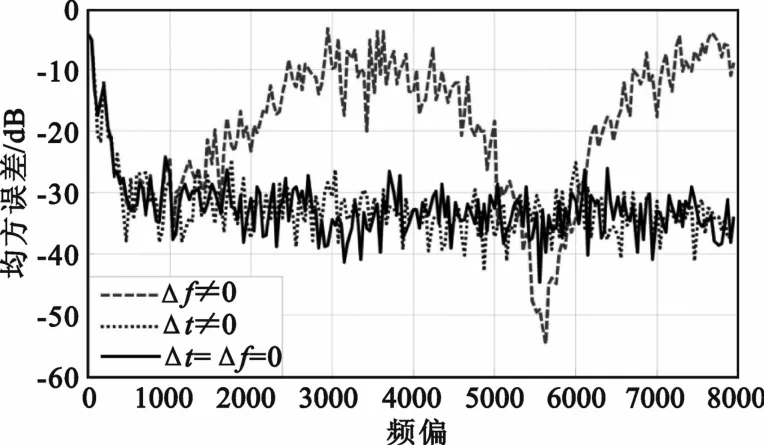
图2 频偏和时延误差对PCMA干扰对消的影响Fig.2 Influence of frequency offset and time delay error on PCMA interference cancellation

4 VFF-RLS自适应对消滤波器

RLS算法是最小二乘算法的递归形式，将指数加权的误差平方和作为代价函数。

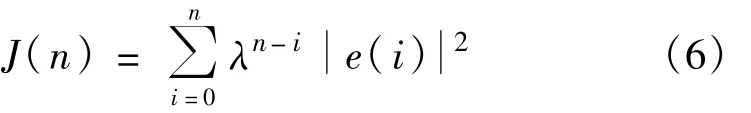
式中，λ为遗忘因子。干扰对消滤波器以重构信号x（n）为输入信号，期望信号d（n）=r（n）。RLS算法如下：

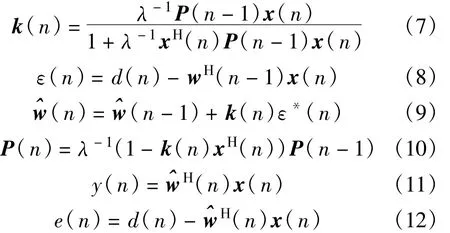
我们的目标是实现信号对消，而不是使误差信号e（n）=0。后验估计误差e（n）的值应为s′2（n）+n（t），考虑到噪声可能被消除，最优解为e（n）= s′2（n）。若遗忘因子λ较小，e（n）趋于零，＾s1（n）≈d（n）=r（n），若λ＞1，会引入大的误差，只有在λ≅1时，滤波器输出信号＾s1（n）≈s1′（n）。因此，在干扰对消应用中，遗忘因子λ应是一个接近1的值。假设λ是时变量且是确定的，即：

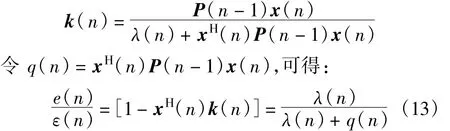
在分析RLS算法时一个比较通用的假设是P（n）独立于x（n）［9］，两边平方求均值，可得：

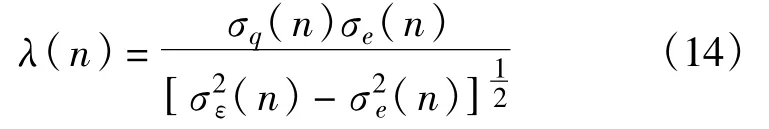
后验误差为目标信号，其均方根变化反映了系统的失调动态。一般地，σ2ε（n）＞σ2e（n），但在干扰对消中，会出现σ2ε（n）＜σ2e（n）的情况，为了避免RLS算法发生较大失调，遗忘因子限制在1附近的一个闭区间，λk∈［λmin，λmax］，则有：

计算中可采用如下递归方式计算：

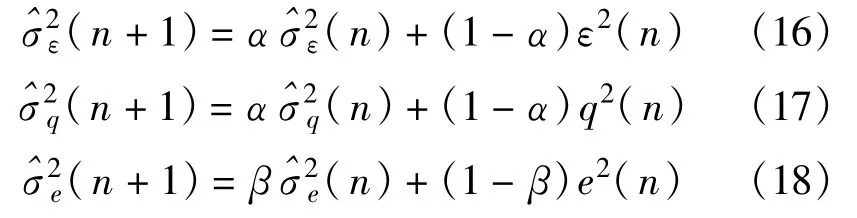
5 模糊函数参数估计算法

对时延和频偏的联合估计通过模糊函数算法实现［10］，当频偏和时延与下行链路信号匹配时，模糊函数会出现尖峰，通过检测尖峰从而达到频偏和时延的估计。

考虑信道时延和频偏，本地回波信号为

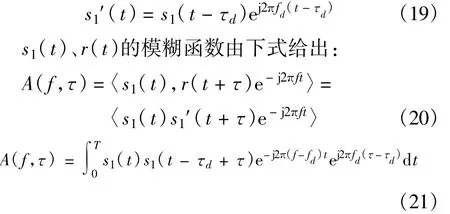
模糊函数为两信号内积的傅里叶变换。当时延和频偏匹配时，即f=fd且τ=τd时，模糊函数将出现最大峰值，即：

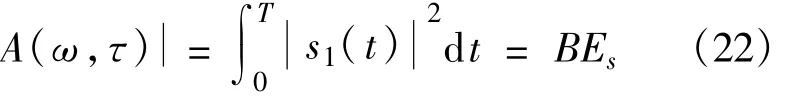
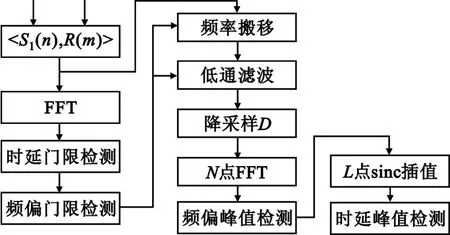
图3 基于模糊函数的频偏和时延估计算法Fig.3 Ambiguity function based frequency offset and delay estimation algorithm

在卫星通信中，多普勒频偏通常远小于采样频率，要达到期望的频率精度需很高的运算量，而时延精度受采样间隔的限制。且在PCMA应用中，只关心频偏和时延值附近的分辨率。降采样的方法可在不增加运算量的同时有效地提高局部频谱分辨率，其前提是数据量足够大。

图3所示算法中互相关运算结果数据长度为ND，将数据分成D段，将这D段数据叠加并计算N点FFT，通过门限检测可得到粗略的时延和频偏估计。将频偏所在频段搬移到低频，在降采样之前，需通过抗混叠低通滤波器。在D倍降采样之后做N点FFT计算，检测其峰值，可得频偏的估计值。相较于ND点FFT直接计算，运算量大大降低。频率分辨率为Δf=FS／ND。对时延估计，采用sinc函数插值法，时间分辨率Δt=TS／L，提高了L倍。

6 仿真实验

我们对PCMA自适应干扰对消算法进行了仿真。假定信道噪声为加性高斯白噪声，PCMA通信系统中本站和远端用户均采用QPSK调制，码速率为1 Mbit／s，符号周期T=10-6s，且均采用升余弦成型滤波器，升余弦滚降系数α1，2=0.4，多普勒频偏fd1，2～U（0，30 kHz），时延τ1，2～U（0，T），均随机产生，采样率Fs=4×106Hz。

自干扰对消算法采用本文给出的VFF-RLS算法，Kα=0.5，Kβ=Kα／10=0.05，遗忘因子λmin= 0.996 5，λmax=0.999 999。自干扰对消误差性能由对消均方误差衡量：10 lg［C（e）］。图4为频偏为1 Hz、时延为0.25×10-6s、信噪比为20 dB时20次实验的平均对消误差曲线，结果表明VFF-RLS算法误差性能曲线较为平坦，具有较低的对消误差和较好的稳健性。图5为相同条件下单次实验的原始波形与对消后的波形对比，显示了自适应干扰对消滤波器消除了时延和频偏对信号的影响，其输出较好地保留了原始信号的波形信息。

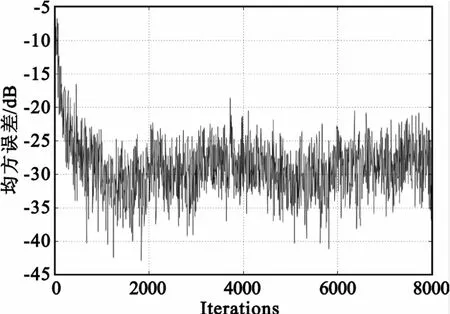
图4 VFF-RLS算法误差性能Fig.4 Error of VFF-RLSalgorithm

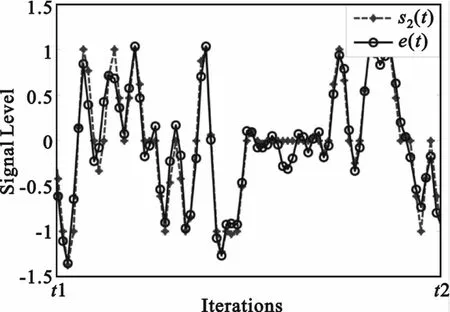
图5 对消波形与原始信号波形Fig.5 Cancelled wave with originalwave

最后，对不同信噪比条件下的对消性能进行了仿真，给出了不同信噪比条件下系统的误码率性能曲线，见图6。基于VFF-RLS算法的自适应干扰对消算法，对于QPSK-PCMA通信系统，其误码率曲线随信噪比增加而减小，随着信噪比的增加，误码率减小程度趋缓，相同误码率所需信噪比，PCMA系统大于单路系统。相较于单路系统，在误码率对通信最重要的10-4处，QPSK-PCMA系统应用该算法只需要2 dB左右的额外功率，对卫星转发器的功率需求较低。

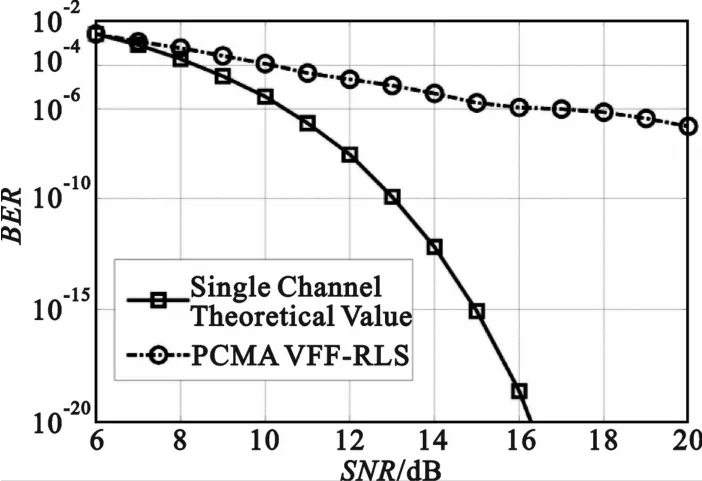
图6 VFF-RLS算法的PCMA系统误码率曲线Fig.6 BER of PCMA system by applying VFF-RLSalgorithm

7 结论

本文分析了参数估计误差对自干扰对消的影响，提出了基于模糊函数和VFF-RLS算法的PCMA自适应干扰对消算法。仿真表明该算法能克服参数估计误差的影响，具有较好的误差性能和稳健性，能够满足PCMA通信要求。VFF-RLS算法实现简单，能适应平稳和非平稳环境，可广泛应用于各种信号处理系统。另外，应用降采样和sinc插值法的模糊函数参数估计算法适合回波信号小的参数估计，具有较好的精度和较低的运算量。

［1］Mark D Dankberg，Mark JMiller，Michael GMulligan.Self -interference Cancellation for Two-party Relayed Communication：United States，520868［P］.1997-01-21.

［2］Glenn D Collins，Don L Anair，Michael JReady.Adaptive Canceller for Frequency Reuse Systems：United States，11／045782［P］.2005-01-28.

［3］Simon Haykin.Adaptive Filter Theory［M］.4th ed.USA：Pearson Education，2002.

［4］Leung S H，So C F.Gradient-based Variable ForgettingFactor RLS Algorithm in Time-varying Environments［J］. IEEE Signal Processing，2005，53（8）：3141-3150.

［5］YazdiH S，YazdiM S，Mohammadi M R.A Novel Forgetting Factor Recursive Least Square Algorithm Applied to the Human Motion Analysis［J］.International Journal of Applied Mathematics and Computer Sciences，2009，5（2）：128-135.

［6］Liu Shunlan，Zhu Fu，Hu Jianhong.Research on Blind E-qualization Algorithm of Modified RLS Based on Canonical Correlation Analysis［C］／／Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing.Kunming，China：CMC，2009：377-380.

［7］Amit Kumar Kohli，Amrita Rai，Meher Krishna Patel.Variable Forgetting Factor LS Algorithm for Polynomial Channel Model［J］.ISRN Signal Processing，2011（2011）：1-4.

［8］Paleologu S，Benesty J，Ciochina S.A Robust Variable Forgetting Factor Recursive Least-Squares Algorithm for System Identification［J］.IEEESignal Processing，2008，15（5）：597-600.

［9］Bottomley G E，Alexander ST.A Novel Approach for Stabilizing Recursive Least Squares［J］.IEEE Signal Processing，1991，SP-39（8）：1770-1779.

［10］Nadav Levanon，Eli Mozeson.Radar Signals［M］.Hoboken，NJ：JohnWiley＆Sons，Inc.，2004.

TIANWen-ke was born in Pingliang，Gansu Province，in 1978.He received the B.S.degree from PLA Information Engineering University in 2001.He is now a graduate student.His research direction is signal processing.

Email：syminy＠gmail.com

王剑（1975—），男，安徽岳西人，讲师，博士研究生，主要研究方向为信号处理；

WANG Jian was born in Yuexi，Anhui Province，in 1975.He is now a lecturer and working toward the Ph.D.degree.His research direction is signal processing.

Email：jian-wang＠tsinghua.edu.cn

山秀明（1944—），男，黑龙江明水人，教授、博士生导师，主要研究方向为信号处理、复杂系统理论应用。

SHAN Xiu-ming was born in Mingshui，Heilongjiang Province，in 1944.He is now a professor and also the Ph.D.supervisor.His research interests include signal processing，theory and application of complex system.

Email：

shanxm＠tsinghua.edu.cn

《电讯技术动态》征稿启事

《电讯技术动态》（月刊）创刊于1972年，是由中国西南电子技术研究所主办的内部刊物，主要报道与下述专业领域相关的国际厂商科研动态；外军先进装备研发、试验和使用情况；学术交流和展会信息。本着服务于国内军工科研的目的，提供国外军事技术与装备的最新发展动态，服务于研发生产为宗旨的办刊原则，将《电讯技术动态》发展成国内以军工电子为主的行业动态是我们长期不懈的目标。

为促进《电讯技术动态》更好地交流与发展，热诚欢迎业内学者、专家及科研人员踊跃投稿。

投稿领域：

来稿要求及注意事项：

（1）文稿务必主题明确，论述合理，逻辑严谨，数据可靠，叙述清楚，文字精炼；

（2）文稿一般不应超过4 000字，尽量提供word文档，对于文中的图片请以附件形式添加发送至指定投稿邮箱；

（3）投稿务必署名，且对于译稿标明原文详细出处；

（4）请务必采用Email投稿，投稿邮箱：dianxundongtai＠163.com。来稿请注明作者详细通信地址、联系电话和有效电子邮箱；

（5）本刊编辑部将在15天之内对来稿作出取舍，可通过电话或电子邮件查询稿件审查情况，如逾期未收到处理意见，作者有权对稿件另行处理。稿件一经刊用，本刊将酌情从优支付稿酬并赠送当期样刊。请勿一稿多投，否则后果自负。

电话：（028）87555634传真：（028）87538378

Adaptive Interference Cancellation for Paired Carrier Multiple Access

TIANWen-ke，WANG Jian，SHAN Xiu-ming
（Department of Electronic Engineering，Tsinghua University，Beijing 100084，China）

Adaptive self-interference cancellation for Paired CarrierMultiple Access（PCMA）is investigated.The influence of parameter estimation error on self-interference cancellation is analysed.The cancellation error is non-stationary with the frequency offseterror′s influence and the classicaladaptive cancellation filter cannot converge to desired weight.A new Variable Forgetting Factor（VFF）Recursive Least Square（RLS）algorithm is proposed.Meanwhile，parameter estimation algorithm with high accuracy and low complexity based on ambiguity function is presented.Simulation results prove the validity of VFF-RLS cancellation algorithm for PCMA system with good cancellation performance，robustness and low excess power requirement.

satellite communication；PCMA；adaptive interference cancellation；VFF-RLSalgorithm

TN911.7

A

10.3969／j.issn.1001-893x.2011.09.016

田文科（1978—），男，甘肃平凉人，2001年于解放军信息工程大学获工学学士学位，现为硕士研究生，主要研究方向为信号处理；

1001-893X（2011）09-0078-05

2011-04-14；

2011-06-10