LDPC 码在非相干BFSK系统中的性能分析✴

戴精科，郭道省，张邦宁，陈雪冰

（1.解放军理工大学通信工程学院，南京210007；2.解放军61068部队；陕西长安710100）

LDPC 码在非相干BFSK系统中的性能分析✴

戴精科1，郭道省1，张邦宁1，陈雪冰2

（1.解放军理工大学通信工程学院，南京210007；2.解放军61068部队；陕西长安710100）

通过理论分析和计算机仿真研究了LDPC码在非相干BFSK系统中的性能。首先证明单输入双输出的非相干BFSK系统满足信道对称条件，然后分别利用离散密度进化（DDE）和高斯近似（GA）算法给出了LDPC码的性能下界，后者与前者相比性能非常接近而且计算量要小很多。通过仿真得到几种常用LDPC码的性能并与译码门限以及香农极限进行了比较，在相同码长条件下，度参数为（3，6）的码字具有最优的性能，并且其译码门限距离香农极限只有约0.67 dB。

LDPC码；非相干检测；BFSK；对称条件；离散密度进化

1 引言

为了实现可靠传输，通信系统通常利用信道编码来纠正信息传递过程中的随机错误。自从Turbo码［1］被提出后，人们发现了很多性能接近香农极限的信道码［2-4］。其中低密度奇偶校验（Low Density Parity Check，LDPC）码具有以下特点［5］：能够并行译码，具有较快的译码速度；存在多种复杂度低的简化译码算法；具有自交织性且能确定译码结果正确与否；误码平层较低，性能接近甚至超过Turbo码。目前，LDPC码在卫星通信特别是深空通信中已经得到了广泛应用。

为了分析信道编码的性能，人们提出了许多方法，其中密度进化（Density Evolution，DE）算法［6-8］是当前分析LDPC编码系统性能的有效工具。只要满足对称性条件［6］，该算法能通过跟踪分析译码器中变量节点和校验节点之间所传递消息的概率密度来判断LDPC码的译码门限，而且还可以设计性能更好的不规则LDPC码［5，9］。对于实际信道DE算法的实现十分复杂，人们提出了多种简化算法，例如离散密度进化（Discrete Density Evolution，DDE）法［10］和高斯近似（Gaussian Approximation，GA）法［11，12］，其中GA算法把迭代中计算消息密度的无限维问题转化为求高斯分布密度函数均值的一维问题，在牺牲很小估计性能的前提下大大减少了运算量。利用DE（简化）算法，文献［5］、［6］研究了加性高斯白噪声（AdditiveWhite Gaussian Noise，AWGN）信道中LDPC码的性能，而文献［13］、［14］则分别分析了其在瑞利和莱斯衰落信道中的性能。

以上文献的研究基本都集中在相干检测的BPSK系统，当载波相位较难估计（例如采用跳频通信体制）时，通信系统往往会采用非相干检测方法［4，15-17］，其中最常见的是差分检测（针对Differential M-ary Phase Shift Keying，DMPSK）和平方律检测（针对Frequency Shift Keying，FSK）。对于差分相位调制系统，文献［15，16］分别研究了LDPC码在AWGN和瑞利衰落信道中的性能。对于FSK系统，文献［4，17］利用外信息转移（Extrinsic Information Transfer，EXIT）图分析了重复累计码、Turbo码的性能；文献［18，19］分别仿真了LDPC码在非相干检测的MFSK和快跳频BFSK系统中的性能，但都未从理论上给出系统的性能界。

目前还没有见到有关分析LDPC码在非相干BFSK系统中理论性能的报道，因此本文将对该系统在AWGN信道中的性能进行研究，给出理论下界并仿真实际码性能。在BPSK或MDPSK系统中，一个输入符号只对应一个信道输出，信道的对称条件能够较好地满足［6，15］，但是对于非相干检测BFSK系统，一个输入对应两个输出，信道的对称性不能够直接得到。因此，我们考察LDPC和积译码器的初始信息——符号的对数似然比（Log Likelihood Ratios，LLRs），证明它满足信道对称条件，可以利用DE（简化）算法来估计系统的理论下界。采用DDE和GA算法发现，LDPC码在非相干检测BFSK系统中具有接近香农极限的性能（例如，相距0.67 dB），而且这两种算法估计的性能非常接近（例如，相距0.05 dB）。最后，通过仿真展示了几种实际LDPC码的性能并得到了一些有意义的结论。

2 系统模型

图1给出了LDPC编码非相干检测BFSK系统模型。

图1 LDPC编码非相干BFSK系统模型Fig.1 Themodel of LDPC coded non-coherent BFSK system

在发送端，LDPC编码后的信息比特被送入BFSK调制器，经历AWGN信道后，在接收端的信号为

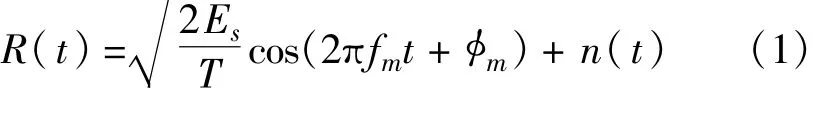
式中，0≤t≤T，m=0，1；Es和T分别为符号能量和持续时间，f0和f1分别是编码后比特为0或1时对应的载波频率，而且满足正交性条件［20］；φm是［0，2π）上均匀分布的随机相位；n（t）为加性白高斯噪声，其双边功率谱密度为N0／2。接收信号经过平方律检测器（解调）后的输出为Ym=Y2m，c+Y2m，s，其中Ym，c和Ym，s分别是检测器的同相和正交分量，且满足均值为、方差为N0／2的高斯分布。不妨设发送端发送的比特为1且对应载波频率f1，随机变量Ym的概率密度函数（PDF）为［19，20］

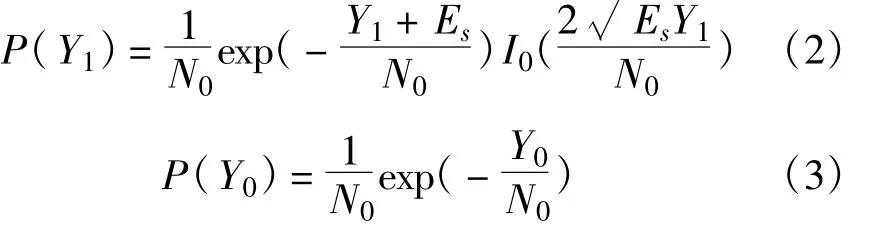
式中，I0（*）为修改的零阶贝赛尔函数。显然，如果发送比特为0，Y1和Y0的PDF正好相反。译码使用和积算法，其输入信息对数似然比为［19］

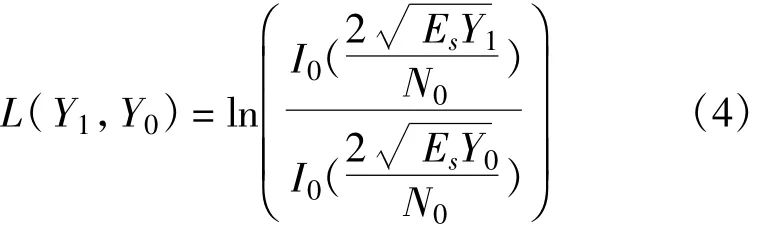
3 密度进化算法和系统性能分析

利用密度进化分析系统性能时必须满足对称条件，其中校验和变量节点的对称性是由译码算法决定，而信道对称性由实际信道决定。从文献［6］可知，和积译码算法可以保证校验和变量节点的对称性，因此，我们重点讨论信道对称性，证明系统的对称条件后假设发送信息为全1码字并利用密度进化分析性能。由式（2）～（4）可知，很难解出和积译码器初始信息L的PDF闭合表达式，不过通过量化随机变量可以求得其概率质量函数（Probability Mass Function，PMF）［10］，并利用离散密度进化获取系统性能。观察L的PMF发现它与高斯分布非常类似，因此也将利用高斯近似来获取系统性能。采用密度进化时存在无环且码长无限的假设，实际系统中LDPC码（本文仅讨论规则LDPC码）都是有环而且长度有限，因此DE（简化）算法得到的门限是实际系统的性能下界［6］。

3.1 信道对称性

对编码比特进行如下映射：1→1，0→-1。对于单输入、单输出的相干解调BPSK系统，信道的对称性由下式保证［6］：

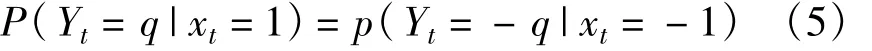
式中，xt为第t个编码比特，而Yt为相应的解调器输出。对于非相干解调的BFSK系统，平方律检测器的输出为Y1和Y0两项，因此其对称性不能用式（5）来保证。和积译码器的初始消息为L，它由PDF分别满足式（2）、（3）的两个随机变量组成（其中第二个分布是参数为N0的指数分布），且发送数据xt（±1）将决定这两个随机变量的相对位置。下面证明L满足对称性条件。

假设L的PDF为P（Lt=l｜xt=1）=q，q的取值由式（2）～（4）决定。发送数据xt=1时，式（4）右边分子中的随机变量Y1的PDF为式（2），分母中的随机变量Y0的PDF为式（3）。发送数据xt=-1时，Y1和Y0的PDF正好相反，所以有P（Lt= -l｜xt=-1）=q。从上述分析可知，非相干检测器传递给译码器的消息可以写为Lt=xtzt，即消息是发送数据与信道转移概率的乘积——此处zt为信道转移概率，定义为Pr（zt=l）=q，与信息比特的取值无关。由文献［6］可知，如果消息Lt的符号随着信息比特符号跳变而发生翻转，系统性能与码字无关，因此单输入双输出的非相干BFSK系统满足对称性条件，可以用全1（或全0）码字来研究LDPC码的性能。

3.2 离散密度进化

3.2.1 初始信息

假设发送信息为全1码字的（dv，dc）规则LDPC码，把式（2）、（3）所示PDF进行量化，可以获得相应的PMF为（Δ为量化间隔，Z为全体整数集合）

因此初始消息L的PMF为

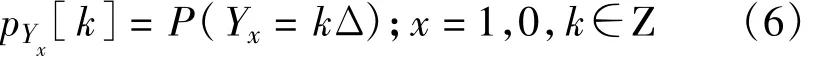
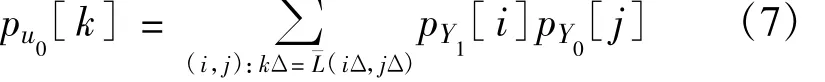
式中，¯L为式（4）的量化函数。根据式（6）、（7）计算出不同比特信噪比（Eb／N0）下的pu0，并把它与均值为m0、方差为2m0高斯分布随机变量的PDF进行比较（如图2所示），其中m0为u0的均值。由图可知，L的PMF与高斯分布的PDF曲线非常接近。

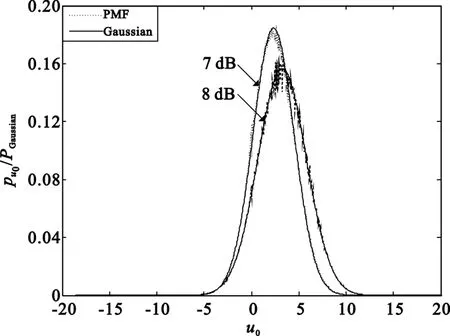
图2 初始消息L的PMF与高斯分布的PDF曲线Fig.2 The PMF and PDF curves of initialmessage L and Gaussian distribution

3.2.2 离散密度进化算法

假设第l次迭代时校验和变量节点的PMF分别为p（l）u、plv（由于每个节点的输入和输出信息都是独立同分布的，所以略去了表示节点度数的角标），则在和积译码算法的迭代中变量和校验节点的输入信息分别为［10］

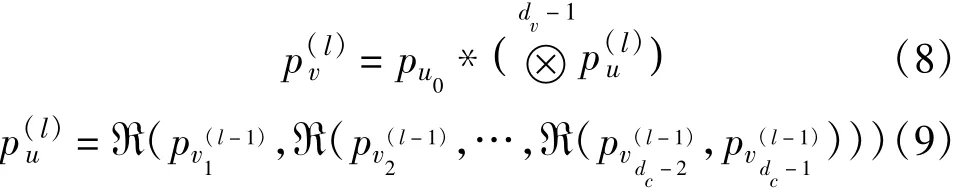
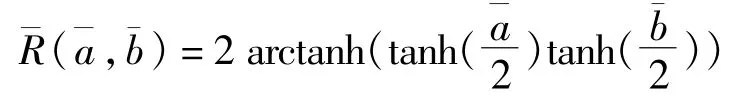
¯a和¯b为量化消息，其PMF为p¯a和p¯b。令¯c=¯R（¯a，¯b），定义R为消息¯c的PMF，则：

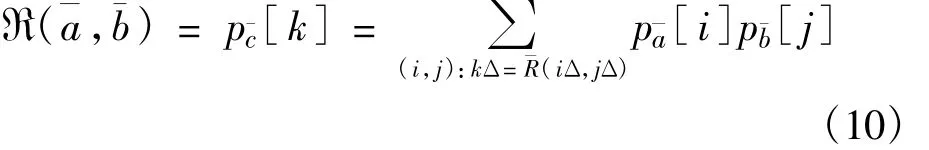
按照和积译码算法，消息在校验和变量节点之间根据式（8）、（9）进行迭代，如果信噪比超过译码门限，随着l的增加，即误码率趋向于0，否则误码率会大于某个非0数值。

图3展示了Eb／N0分别为7.32 dB、7.33 dB和7.40 dB时变量节点消息的PMF进化曲线，且随着l的增加曲线从左向右“移动”。计算中设dv=3，dc或l到达100。由图可知，当信噪比为7.32 dB时，随迭代次数的增加下降很慢且趋向于一个非0定值；当信噪比大于7.33 dB时随迭代次数的增加而趋向于0，而且信噪比的增加会减少所需迭代次数。通过离散密度进化我们得到系统的门限约为7.33 dB，与香农极限仅有0.62 dB的差距。

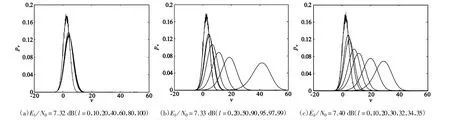
图3 使用离散密度进化时变量节点消息的PMF进化Fig.3 The PMF evolution of variable nodes′messagewhen using DDE

3.3 高斯近似

虽然离散密度进化可以获取系统的门限，但计算量比较大［10］。由图2可知，译码器的初始信息与高斯分布非常类似，因此我们可以利用高斯近似［11］来求取系统的译码门限，这样在译码迭代中只需要计算变量和校验节点消息的均值mv、mu即可。获得初始信息均值mu0有两种方法：一种是利用初始消息L的PMF（式（7）），得到mu0=∫pu0u0d u0；另一种方法是通过仿真实际信道中L的数值并取平均来得到mu0。本文选用第二种方法。

在得到mu0后，高斯近似算法中变量节点和校验节点输入消息的进化式如下所示：

迭代进行到一定次数后，节点消息的均值不再发生变化，此时停止迭代，系统误码率且概率密度函

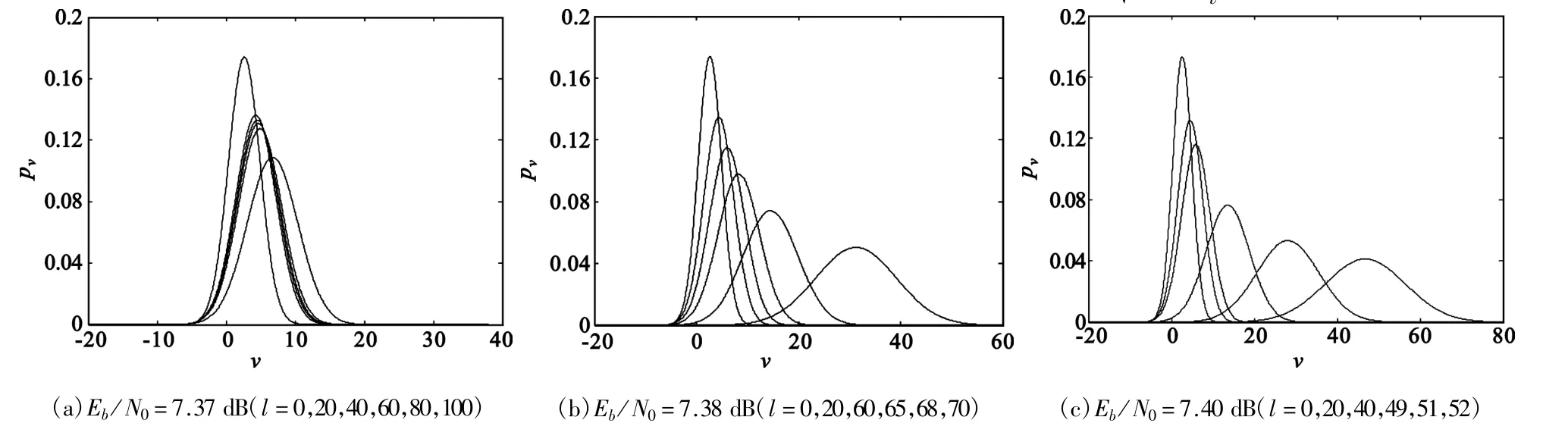
图4 使用高斯近似时变量节点消息的PDF进化Fig.4 The PDF evolution of variable nodes′messagewhen using GA

图4展示了信噪比分别为7.37 dB、7.38 dB和7.40 dB时变量节点消息的PDF进化曲线，对它的分析与图3类似，此处不再赘述。值得注意的是，此时系统的门限为7.38 dB，与离散密度进化获得的门限只相差0.05 dB，因此GA相对于DDE牺牲的性能很小。

4 仿真结果

基于图1所示模型，我们对LDPC码在系统中的性能进行计算机仿真，码字的校验矩阵由渐进边长增长（Progressive Edge-Growth，PEG）算法产生，码率为0.5。CL表示LDPC码的环长，一般来说在相同码长条件下，校验矩阵中的度参数（dv，dc）越小，环长越大。Shannon limit表示非相干检测BFSK系统的香农极限，Threshold是采用高斯近似得到的系统译码门限，N为码长，Ber／Per表示系统的误码率与误包率之比，和积译码算法的最大迭代次数为100。

图5给出了具有不同码长的（2，4）LDPC码在非相干BFSK系统中的性能。由图可知，系统性能随着码长的增加越来越接近译码门限，这说明高斯近似算法能够很好的预测性能。但是Threshold距离香农极限还有大约2.5 dB的差距，这是因为码字的校验矩阵中行、列的重量（1的个数）较小，校验译码能力不强。

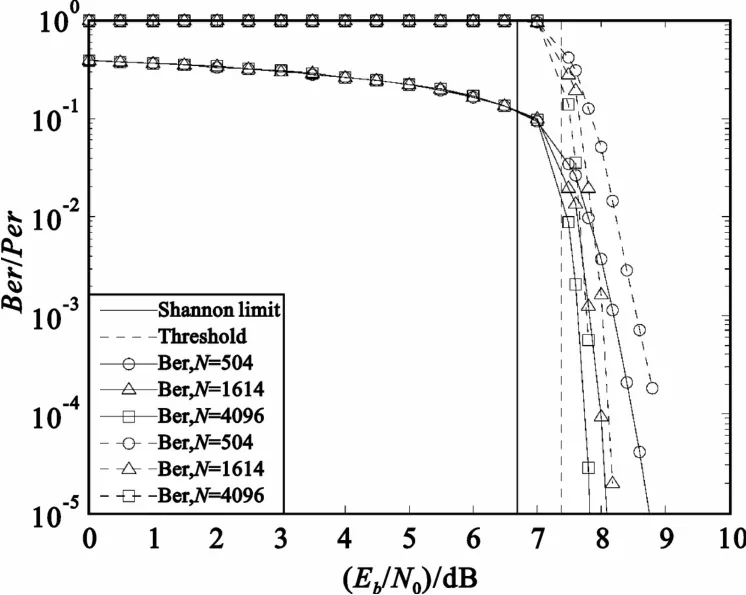
图6 （3，6）LDPC码的性能（CL=8）Fig.6 The performance of（3，6）LDPC code（CL=8）

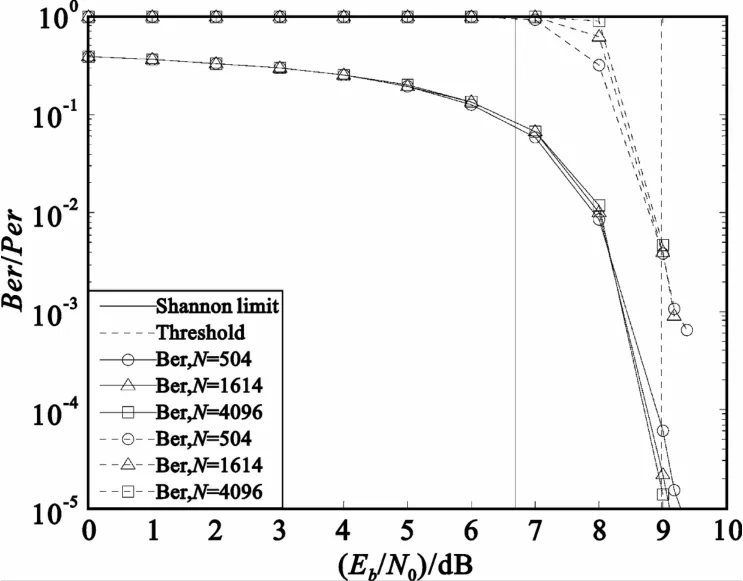
图5 （2，4）LDPC码的性能（CL=10）Fig.5 The performance of（2，4）LDPC code（CL=10）

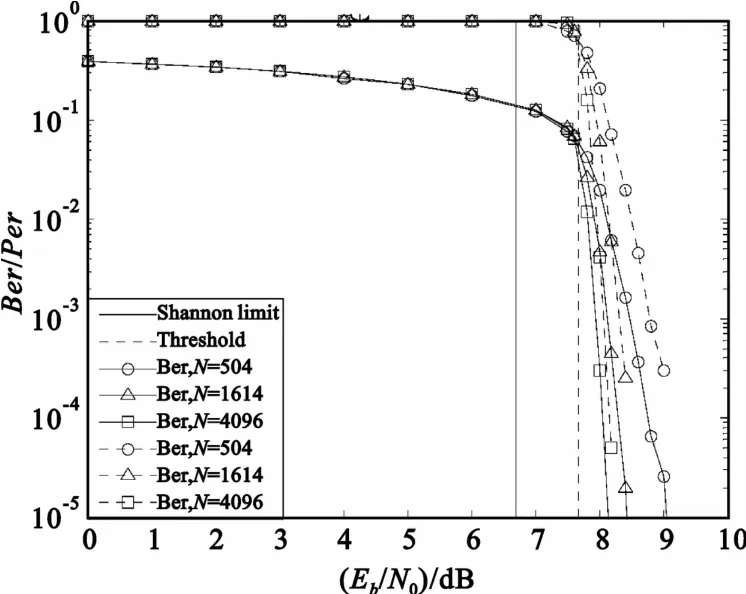
图7（4，8）LDPC码的性能（CL=6）Fig.7 The performance of（4，8）LDPC code（CL=6）

图6 和图7分别展示了具有不同码长的（3，6）和（4，8）LDPC码在非相干BFSK系统中的性能。随着码长增加，系统性能趋近于高斯近似算法所给出的门限，而且在相同码长情况下，环长CL=8的码字性能要优于CL=6的码字。值得注意的是，比较图5和图6可知，尽管（2，4）LDPC码的环长CL= 10，大于（3，6）LDPC码的环长，但在相同码长条件下的性能较差，这说明码字性能与环长和度参数都有关系。比较图5～7，（3，6）LDPC码的性能在码长相等的条件下比其它两种码字的要好，由高斯近似获得的理论译码门限距离香农极限只有大约0.67 dB。另外，如果CL为定值，N越大，系统性能与门限之间的距离越小；如果N为定值，则CL越大，距离越小，这主要是因为密度进化理论中无限码长以及无环（CL→+∞）的假设。

5 结论

本文较全面地研究了AWGN信道下具有不同度参数和码长的LDPC码在非相干BFSK系统中的性能，证明了单输入双输出的非相干BFSK系统仍然满足信道对称条件，并利用离散密度进化和高斯近似算法求得（3，6）LDPC码的译码门限，它与香农极限非常接近；仿真了几种LDPC码性能并与其译码门限进行比较验证，同时讨论了度参数、码长、环长等因素对系统性能的影响。在未来的工作中，可以根据密度进化的思想探寻衰落信道下LDPC编码BFSK系统的性能，并设计出具有更好性能的不规则LDPC码。

［1］Berrou C，Glavieux A，Thitimajshima P.Near Shannon limit error-correcting coding and decoding：Turbo-codes［C］／／Proceedings of IEEE International Conference on Communications.Geneva，Switzerland：IEEE，1993：1064-1070.

［2］MacKay D JC.Good error-correcting codes based on very sparsematrices［J］.IEEE Transactions on Information Theory，1999，45（3）：399-431.

［3］Zhang Q，Le-Ngoc T.Turbo product codes for FH-SS with partial-band interference［J］.IEEE Transactions on Wireless Communications，2002，1（3）：513-520.

［4］Fabregas A G，Grant A J.Capacity approaching codes for non-coherentorthogonalmodulation［J］.IEEE Transactions on Wireless Communications，2007，6（11）：4004-4013.

［5］Richardson T J，Shokrollahi M A，Urbanke R L.Design of capacity-approaching irregular low-dnesity parity-check codes［J］.IEEE Transactions on Information Theory，2001，47（2）：619-637.

［6］Richardson TJ，Urbanke RL.The capacity of low-density parity-check codes under message-passing decoding［J］.IEEE Transactions on Information Theory，2001，47（2）：599-618.

［7］Martalo M，FerrariG，Abrarbo A，etal.Density evolutionbased analysis and design of LDPC codes with a priori information［C］／／Proceedings of Information Theory and ApplicationsWorkshop.San Diego，CA：IEEE，2010：1-9.

［8］Tan B S，Li K H，Teh K C.Performance analysis of LDPC codes with selection diversity combining over identical and non-identical Rayleigh fading channels［J］.IEEE Communications letters，2010，14（4）：333-335.

［9］Saeedi H，Banihashemi A H.On the design of irregular LDPC code ensembles for BIAWGN channels［J］.IEEE Transactions on Communications，2010，58（5）：1376-1382.

［10］Chung SY，Forney GD，Richardson T J，etal.On the design of Low-Density Parity-Check codes within 0.0045 dB of the Shannon limit［J］.IEEECommunications letters，2001，5（2）：58-60.

［11］Chung SY，Richardson T J，Urbanke R L.Analysis of sum -product decoding of Low-Density Parity-Check codes using a Gaussian approximation［J］.IEEE Transactions on Information Theory，2001，47（2）：657-670.

［12］LiG，Fair IJ，KrzymienW A.Density evolution for nonbinary LDPC codesunder Gaussian approximation［J］.IEEETransactions on Information Theory，2009，55（3）：997-1015.

［13］Hou J，Siegel PH，Milstein L B.Performance analysis and code optimization of Low Density Parity-Check codes on Rayleigh fading channels［J］.IEEE Journalon Selected Areas in Communications，2001，19（5）：924-934.

［14］林家儒，吴伟陵.非规则LDPC码在RICE信道中的性能分析［J］.电子学报，2005，（33）1：43-46. LIN Jia-ru，WUWei-ling.Performance of irregular LDPC codes on Rician-fading channels［J］.Acta Electronica Sinica，2005，（33）1：43-46.（in Chinese）

［15］Jin H，Richardson T J.Design of Low-Density Parity-Check codes for noncoherent MPSK communication［C］／／Proceedings of IEEE International Symposium on Information Theory.Lausanne，Switzerland：IEEE，2002：169.

［16］Nam V T，Kam PY，Xin Y.LDPC codeswith BDPSK and differential detection over flat Rayleigh fading channels［C］／／Proceedings of Global Telecommunications Conference.Washington，DC：IEEE，2007：3245-3249.

［17］ValentiM C，Cheng S.Iterative demodulation and decoding of Turbo-coded M-ary noncoherent orthogonalmodulation［J］.IEEE Journal on Selected Areas in Communications，2005，23（9）：1739-1747.

［18］Supakwong S，Wilson SG.LDPC coded M-ary orthogonal signaling with noncoherent detection［C］／／Proceedings of Conference on Information Sciencesand Systems.Baltimore，MD：The Johns Hopkins University，2005.

［19］Wu X，Zhao C，You X，L，etal.Robustdiversity-combing receivers for LDPC coded FFH-SSwith partial-band interference［J］.IEEE Communications Letters，2007，11（7）：613-615.

［20］Proakis JG.Digital communications［M］.4th ed.Beijing：Publishing House of Electronics Industry，2006.

DAI Jing-ke was born in Changde，Hunan Province，in 1984.He received the B.S.degree from PLA University of Science and Technology in 2006.He is currently working toward the Ph.D. degree.His research interests include satellite communications and channel coding.

Email：daijingke1984＠163.com

郭道省（1973—），男，河南南阳人，2002年于解放军理工大学获博士学位，现为副教授，主要研究方向为卫星通信与通信抗干扰技术；

GUO Dao-xing was born in Nanyang，Henan Province，in 1973.He received the Ph.D.degree from PLA University of Science and Technology in 2002.He isnow an associate professor.His research interests include satellite communications and anti-jamming communications.

张邦宁（1963—），男，江苏南京人，教授、博士生导师，主要研究方向为卫星通信、信号处理、调制、信道编码和通信抗干扰；

ZHANG Bang-ning was born in Nanjing，Jiangsu Province，in 1963.He is now a professor and also the Ph.D.supervisor.His research interests include satellite communications，signal processing，modulation，channel coding and anti-jamming communications.

陈雪冰（1982—），男，江西人，助理工程师，主要研究方向为信号处理。

CHEN Xue-bing was born in Jiangxi Province，in 1982.He is now an assistant engineer.His research direction is signal processing.

Performance Analysis of LDPC Code in Non-coherent BFSK Systems

DAI Jing-ke1，GUO Dao-xing1，ZHANGBang-ning1，CHEN Xue-bing2
（1.Institute of Communications Engineering，PLA University of Science＆Technology，Nanjing 210007，China；2.Unit61068 of PLA，Chang′an 710100，China）

The performance of low density parity check（LDPC）code in non-coherent binary frequency shift keying（BFSK）system is investigated by theoretical analysis and computer simulation.It is shown that the symmetry conditions are fulfilled in the system with one input and two outputs，and then the lower bound of LDPC code is given by discrete density evolution（DDE）and Gaussian approximation（GA），respectively.The performances of the two algorithms are very close to each other，though the later costsmuch less computation.The performances of certain LDPC codes in common use are obtained by simulations，which are also compared with the decoding threshold and Shannon limit.As long as the code lengths are equal to each other，the（3，6）code has the best performance，and the decoding threshold is approximate 0.67 dB within the Shannon limit.

low density parity check（LDPC）code；non-coherent detection；binary frequency shift keying（BFSK）；symmetry conditions；discrete density evolution

TN911.22

A

10.3969／j.issn.1001-893x.2011.07.014

戴精科（1984—），男，湖南常德人，2006年于解放军理工大学获学士学位，现为博士研究生，主要研究方向为卫星通信与信道编码；

1001-893X（2011）07-0067-06

2011-03-01；

2011-04-08