基于特征点的运动汽车跟踪算法研究

王进花 曹洁

(兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050)

0 引言

在视觉目标跟踪算法中，实时性和准确性是衡量算法好坏的两个重要指标，已有的跟踪算法归纳起来主要有［1］［2］:基于 3D立方体模型的跟踪算法，基于变形模型的跟踪算法，基于区域的跟踪算法，基于光流的跟踪方法以及基于特征的跟踪算法等。这些算法都有各自优势，但是在复杂背景中，目标存在遮挡或阴影干扰时，要实现对运动目标准确、实时地跟踪，是目前目标跟踪中需要解决的难点问题。

本文采用特征点结合自适应卡尔曼滤波(AKF)算法实现运动汽车跟踪。考虑到跟踪的实时性，首先，在目标定位时通过卡尔曼滤波算法估计目标在下一帧图像中的位置，减小搜索范围，提高运算速度;然后，在预测位置范围内提取车辆特征点，将目标当前候选特征点与模板特征点进行匹配，确定目标的精确位置，提高跟踪的准确性。通过交通视频仿真实验，证明该算法在快速跟踪机动目标时效果较好。

1 汽车运动模型和滤波算法

1.1 汽车运动模型

近年来，国内外学者专家对目标运动模型做了大量的研究并取得了诸多成果，其中“当前”统计模型［3，4］得到了越来越广泛的应用。此模型的思想是:当目标正在以某一加速度机动时，加速度在下一时刻的取值是有限的，并且只能在“当前”加速度的邻域内。其本质上是非零均值时间相关模型，加速度的“当前”概率密度符合瑞利分布，均值为“当前”加速度预测值，随机加速度符合一阶时间相关过程，即

1.2 滤波算法

1.2.1状态方程

设采样周期为T，可得到(3)式的离散化状态方程为:

其中，状态向量

设当前加速度均值为

则可得到预测表达式为

式(4)中W(k)是离散时间白噪声序列，其协方差矩阵为

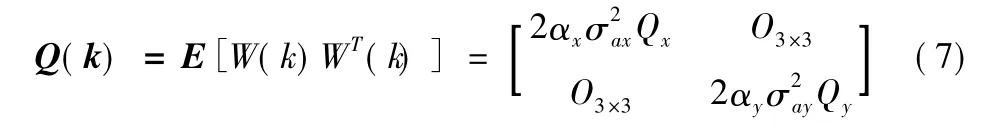
其中，

qij(i，j=1，2，3)可参考文献［5］。分别为x，y方向的加速度方差;αx，αy分别为x，y方向的目标机动频率。

由文献［6］k时刻加速度最大值和方差分别可表示为式(8)和(9)。

1.2.2观测方程

其中，

VZ(k)是均值为零，方差为R(k)的高斯白噪声。

1.2.3自适应卡尔曼滤波算法

根据状态方程和观测方程，可以得到自适应Kalman滤波方程为

2 特征点的提取及匹配

2.1 特征点提取

现有的角点检测算法可分为两类［7］:1)灰度级图像数据检测法;2)目标边缘信息检测法。本文采用基于图像灰度的角点检测算法，其中Harris角点检测算法［8，9］，其计算简单、提取的特征点均匀合理、可靠性高，因而在图像处理领域得到了非常广泛的应用。

图像的自相关函数描述了局部灰度的变化程度，因此，角点与自相关函数的曲率特性有关，图像自相关函数表示为:

式中，Ix+u，y+v，Iu，v分别为图像中点 (x+u，y+v)和(u，v)对应的灰度值。对(16)式在点(u，v)进行二元函数的泰勒展开，可得到自相关函数E(x，y)的近似泰勒多项式

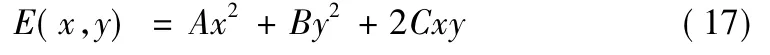
其中

w为高斯函数

则Harris角点检测器为

令k=0.04，即经验值，R取合理的阈值即可得所求角点。阈值取决于实际图像的属性，如尺寸、纹理等，也可以通过确定图像中可能的特征点的数量，并取其R值较大的像素点作为特征点。考虑到运算速度和目标表示的准确性，需要合理确定特征点的数目。本文提取特征点数目设定为5～15。

2.2 特征点匹配

2.2.1建立目标模板

根据目标检测结果计算初始帧中目标形心坐标，设为(x0，y0)，并计算每个特征点(xi，yi)相对于目标形心的偏移量(Δxi，Δyi)及灰度值 f(xi，yi)，由偏移量和灰度值构成模板特征点像素集合:

在汽车运动过程中会由于转弯、遮挡而发生形变，此时特征点模板与实际目标不符，需要更新，则以当前图像为首帧重新建立目标模板。

2.2.2特征点匹配

根 据2.2 的滤波算法预测车辆在下一帧中的形心坐标以及区域，并在此区域提取当前帧中车辆特征点，从而得到候选特征点的坐标集合。

设 当前帧形心坐标的预测值为(xt，yt)，则目标模板的第i个特征点(xi，yi)坐标的预测值是(xt+ Δxi，yt+Δyi)，在当前帧中以此坐标为中心的5*5的区域内计算特征点(xi，yi)与候选特征点的匹配值R(i，j)，R最小的候选特征点即为模板第i个特征点的匹配点。计算公式如下

图1 跟踪算法流程

图2 跟踪仿真结果

其中，I0(xi，yi)，I(mj，nj)分别为模板第 i个特征点和当前图像第j个特征点的灰度值。在特征提取时，设定提取特征点数是5～15，特征分布较为稀疏并且均匀，在5*5的范围内基本只有1～2个候选特征点，因此匹配计算量小，而且克服了由于预测误差而引起的误匹配及漏匹配，匹配正确率高。

3 基于特征点的运动汽车跟踪流程

图1是算法流程图，首先初始化背景和滤波器，对输入图像进行检测处理，得到目标中心坐标，并提取目标特征点，建立目标模板;其次，采用AKF滤波算法预测目标中心在下一帧图像中的位置，在此区域提取当前帧目标特征点，进行特征点的匹配，依据匹配结果更新目标当前位置;最后，根据相关准则判断是否需要更新模板，若不更新则处理下一帧图像，循环工作。否则由当前帧重新建立模板，然后转到下一帧图像进行循环处理。

4 仿真结果及分析

仿真试验采用兰州市某路口的监控视频图像，通过格式转换得到640×480bmp的序列图像。实验设备采用台式PC机(Pentium Ⅳ，1.70 GHz，512 M 内存)，利用 Matlab7.1仿真软件进行仿真验证。采样周期为0.04 s。

采用本算法跟踪图2所示视频场景中的红色小汽车。图2(a)～(d)是随机截取的四帧不同图像的跟踪仿真结果，图中虚线框是滤波估计位置，‘+’是在当前帧图像中提取的车辆特征点，‘O’为正确匹配特征点。由图可见，特征点正确匹配率较高，只有个别特征点是在车辆转弯形变情况下出现的新增特征点，没有找到匹配点。这种情况可通过模板更新来解决，当特征点的正确匹配率小于设定阈值时更新模板。试验结果验证了该算法的有效性。

5 结束语

本文通过对跟踪过程中方法算法的分析，提出了一种基于特征点和自适应kalman滤波相结合的跟踪方法，通过仿真实验证明该算法的跟踪性能良好。因受外界环境干扰，实际采集到的视频图像质量较差，不利于目标检测及特征提取，因此，首先要对原始图像进行相关的处理。另外，在实际应用中，考虑到目标运动的随机性，能够实时自适应调整目标机动频率因子，使其随目标运动状态的变化而变化，从而得到更佳的跟踪效果，需要合理建立目标机动判别函数。

［1］侯志强，韩崇昭.视觉跟踪技术综述［J］.自动化学报，2006，32(4):603-617.

［2］马安国，罗德林，等.基于“当前”统计模型的目标状态估计［J］.自动化技术与应用，2006，25(7):5-8.

［3］刘海燕，赵宗贵，等.“当前”统计模型机动目标跟踪的改进算法［J］.军事运筹与系统工程，2007，1(1):51-54.

［4］方青，梅晓春.用于机动目标跟踪的Kalman滤波器的设计［J］.雷达科学与技术，2006(1):50-55.

［5］杨万海.多传感器数据融合及其应用［M］.西安:西安电子科技大学出版社，2004:50-51.

［6］王进花，曹洁.基于改进“当前”统计模型和AKF的机动目标跟踪［J］.兰州理工大学学报，2010(4):98-101.

［7］王向军，王研，等.基于特征角点的目标跟踪和快速识别算法研究［J］.光学学报，2007(2):360-364.

［8］刘荆桥，戴光明.角点检测在车辆特征提取中的应用［J］.软件导刊，2008(4):91-92.

［9］郑林，刘泉.一种基于特征点的跟踪算法［J］.武汉理工大学学报，2006(3):398-400，462.