微积分基本公式的简明证法及其应用

严永仙

微积分基本公式是一元函数积分学非常重要的一个公式,在理论上,它将两个完全不同的概念(原函数与定积分)紧密联系在一起;在实践中,它为定积分的计算提供了非常简便而有效的方法。在通用教材[1-5]中,该公式的证明都是以积分上限函数及其导数的相关知识为基础的。然而,从笔者长期的教学实践来看,由于此函数表达式不具体,只是一个抽象的符号∫xaf(t)d t,学生对积分上限函数概念的理解存在着很大的困惑,而对这一新型函数的求导法则更是难以理解和掌握。这一点可从课堂教学的现场反应及学生的作业和卷面情况得到反馈,可以说是错误百出,问题非常严重,这对积分学这块内容的学习和掌握非常不利。这一现象也一直促使笔者思考着一个问题:能否找到一条有效途径,让学生能真正理解积分上限函数的概念并掌握其求导法则,从而可以驾驭这类函数参与普通函数所讨论过的相关问题,如求极限、导数、极值、最值、讨论单调性、不等式的证明等。通过笔者长期的教学实践与摸索,找到了该问题解决的办法,笔者对教材中这节内容进行了较大的处理,打破常规思路,不完全按照教材中的顺序讲解,在引例“求变速直线运动的距离”之后,直接证明得到的结论具有一般性,即给出微积分基本公式的证明,然后引出积分上限函数的定义,再给出其求导法则及相应的证明。笔者在所教的平行班中,采用新旧两种教法进行对比实验,结果发现采用新方法教学效果理想,学生普遍感到好理解,易接受。事实上,采用新方法讲解,思路更连贯,思维不会有很大的跳跃。

1 微积分基本公式的一个简明证法

微积分基本公式的证明,无论是高等数学教材,还是数学分析教材,无一例外都是建立在积上限函数的概念及其导数的知识上加以证明的。下面直接利用定积分的定义结合微分中值定理给出简明证法。

定理1.1 如果函数F(x)是连续函数 f(x)在[a,b]上的一个原函数,则

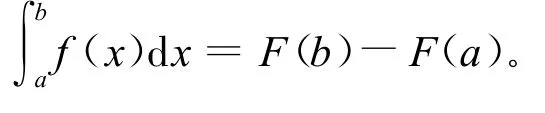
上式称为微积分基本公式。

分析:由定积分的定义,它是特殊和式的极限,把和式中的 f用 F′)代替,看结构联想微分中值定理,最后轻松得到证明思路。

证明 在[a,b]中任意插入若干个分点a=x0＜x1＜x2＜…＜xn-1＜xn=b,得

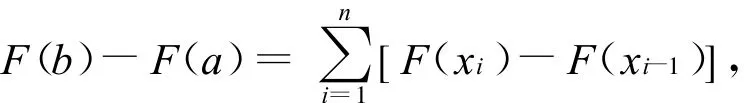
因为F(x)在[a,b]上可导,所以F(x)在每一小区间[xi-1,xi](i=1,2,…,n)上也可导,且F′(x)=f(x),由微分中值定理,得

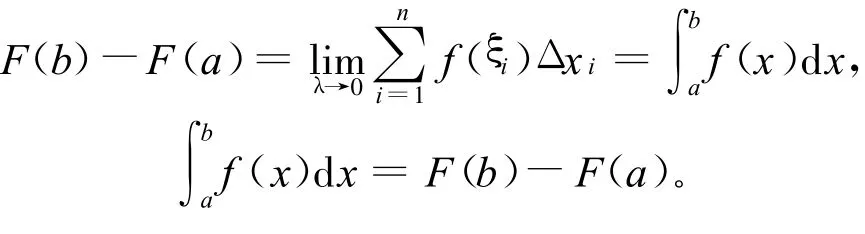
即

从以上证明过程来看,本定理的条件可减弱,于是得下面的定理:

定理1.2[6-7]函数f(x)在[a,b]上可积,F(x)在[a,b]上连续,在(a,b)内除有限个点外处处可导,且 F′(x)=f(x),则

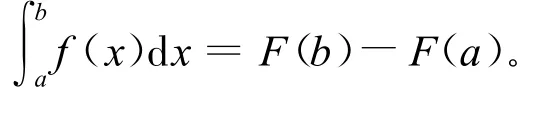
说明:在定理1.1的证明过程的开始部分:在[a,b]中任意插入分点时,只需将F(x)的不可导点一并加入作为分点,后面的过程保持不变,就可得到本定理的证明(证明过程略)。

本证法没有难点,只要思路分析到位,学生容易接受。

有了微积分基本公式,就可以计算定积分,同时可用来证明积分中值定理,下面给出微积分基本公式的新用途。

2 微积分基本公式的新用途

2.1 解释定积分的值与积分变量的选取无关

定理2.1 设 f(x)在[a,b]上可积,且满足定理1.1或定理1.2中的条件,则

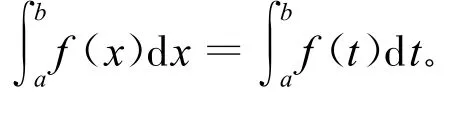
证明 设F′(x)=f(x),由微积分基本公式,得

所以

即定积分的值与积分变量的选取无关。

进一步可得

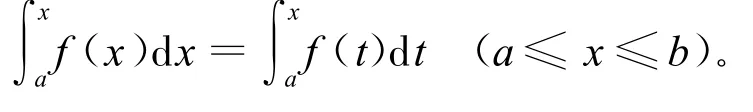
2.2 有助于理解积分上限函数的概念

定义2.1 设函数 f(x)在[a,b]上连续,记

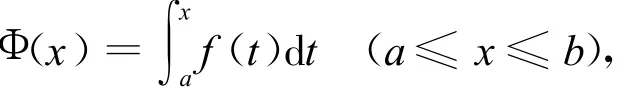
称函数Φ(x)为积分上限的函数。

由微积分基本公式,得

说明:尽管在上式中,F(x)-F(a)仍然是一个抽象函数,但由它来理解Φ(x)为积分上限x的函数,要比由f(t)d t来理解Φ(x),难度大大降低,学生易理解、能接受,进一步可解开学生的疑惑:为什么在函数(x)d x表达式中,积分上限中的x与被积表达式中的x是完全不同的含义。

2.3 给出积分上限函数求导法则的新证法

定理2.2 设函数 f(x)在[a,b]上连续,则 Φ(x)=∫xaf(t)d t(a≤x≤b)在[a,b]上可导,且

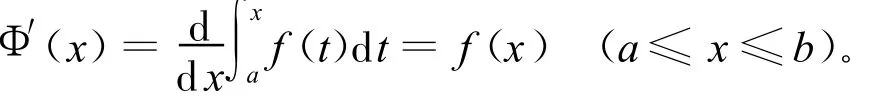
证明 设F′(x)=f(x),x∈[a,b],由微积分基本公式,得

于是有

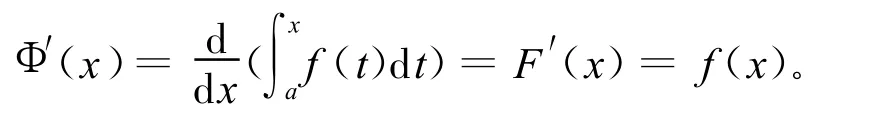
注:1)教材中采用导数的定义式证明Φ(x)可导,学生普遍感到抽象难懂,很难接受。而在文献[8]中,利用函数连续的定义和定积分的保序性给出了此定理的另一种证法。相比较,本文给出的证法更简单,学生更易理解和接受。2)需向学生强调积分上限函数的求导是不需要积分的,直接按定理2.2进行求导即可。虽然先积分再求导在理论上可行(学生习惯用这种方法求导),但很多情况下行不通,如对下列函数:等。

定理2.3 设函数 f(x)在[a,b]上连续,φ1(x),φ2(x)在[a,b]上可导,则

证明 设F′(x)=f(x),x∈[a,b],

由微积分基本公式,得

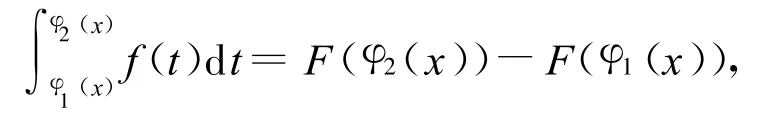
于是由函数和的求导法则及复合函数的求导法则,得

定理2.3的特殊情形如下:

推论2.1 设函数 f(x)在[a,b]上连续,φ(x)在[a,b]上可导,则

将推论2.1中的1)与普通函数的复合函数的求导法则作对比,可以发现它们的相似之处。

3 结 语

本文给出的微积分基本公式的简明证法,思路清晰,方法简单。同时利用它来证明积分上限函数的求导法则非常方便,学生容易理解和掌握。学生看到这种形式的函数参与求极限、导数,讨论单调性、积分不等式的证明等,心理上就不会感到恐惧和焦虑,而是有足够的信心去面对和解决了。

[1] 同济大学数学教研室.高等数学:上册[M].6版.北京:高等教育出版社,2007:139-140.

[2] 吴赣昌.高等数学:上册[M].北京:中国人民大学出版社,2009:228-231.

[3] 欧阳光中,朱学炎,金福临,等.数学分析:上册[M].3版.北京:高等教育出版社,2007:305-307.

[4] 刘玉琏,傅沛仁,林玎,等.数学分析讲义:上册[M].5版.北京:高等教育出版社,2008:413-416.

[5] 陈继修,於崇华,金路.数学分析:上册[M].2版.北京:高等教育出版社,2004:294-297.

[6] 华罗庚.高等数学引论:上册[M].北京:科学出版社,1997:302.

[7] 王艮远.关于微积分基本定理的几点注记[J].武汉工业学院学报,2004,23(4):112-113.

[8] 杨翰深,熊大生.微积分基本定理的一个证明和理解[J].工科数学,2001(2):98-100.