具有两个独立参数的Hardy型积分不等式

陈广生

1 引 言

设L2(0,∞)为实空间,f(x),g(x)∈ L2(0,∞),且则有如下著名的Hilbert积分不等式[1]:

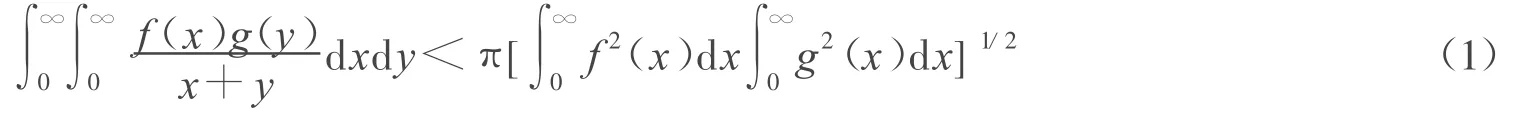
这里,常数因子π是最佳值。

1925年,Hardy[2]引入一对共轭指数(p,q),即1/p+1/q=1,将式(1)推广为

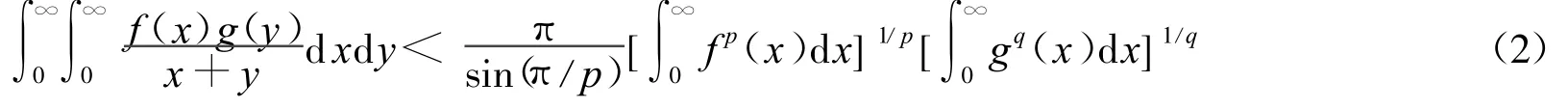
Hardy[1]还建立了式(2)的如下等价式:

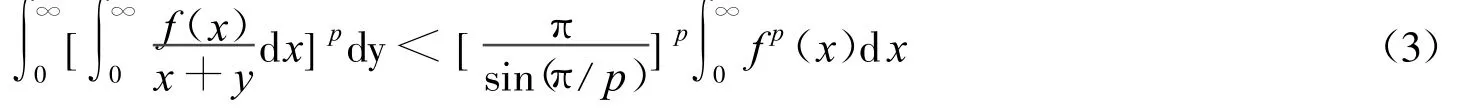
适当变化式(3)的核及积分区间,Hardy[3]建立了如下具有最佳常数因子的Hardy积分不等式:

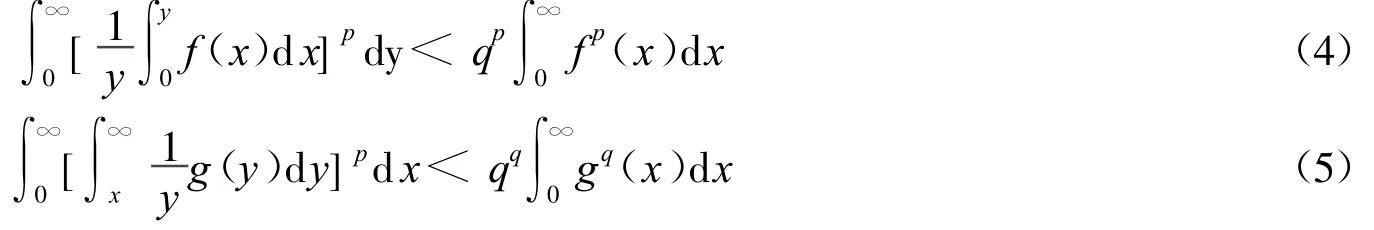
式(1)～(5)在分析学中有重要的应用[4]。文献[5]和文献[6]引入单参量及2对共轭指数(p,q),(r,s),将不等式(2)推广为如下形式:

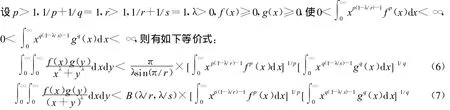
文献[7]利用参量化思想,将式(4)和式(5)进行推广,给出了如下的Hardy型积分不等式。

设p＞1,1/p+1/q=1,r＞0,(r≠1),1/r+1/s=1,λ＞0,f(x)≥0,g(x)≥0,使0＜,则有如下等价式:

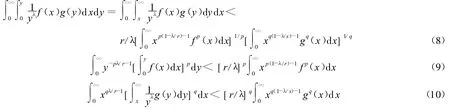
这里,常数因子r/λ,[r/λ]p和[r/λ]q均为最佳值。

本研究的目的是通过引入2个独立参数λ1,λ2,利用权函数方法和实分析技巧,建立式(8)、(9)和(10)的推广式,证明其常数因子为最佳值,并给出一些特殊结果。

2 主要结果

定理1 设 λ1,λ2＞0,p ＞1,r＞0(r≠1),1/p+1/q=1,1/r+1/s=1,f(x),g(x)为(0,∞)上的非负可测函数,且则有如下积分不等式:

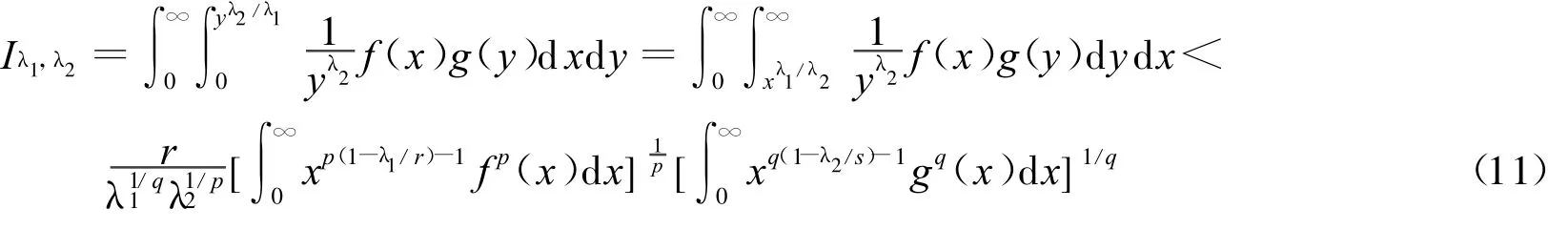
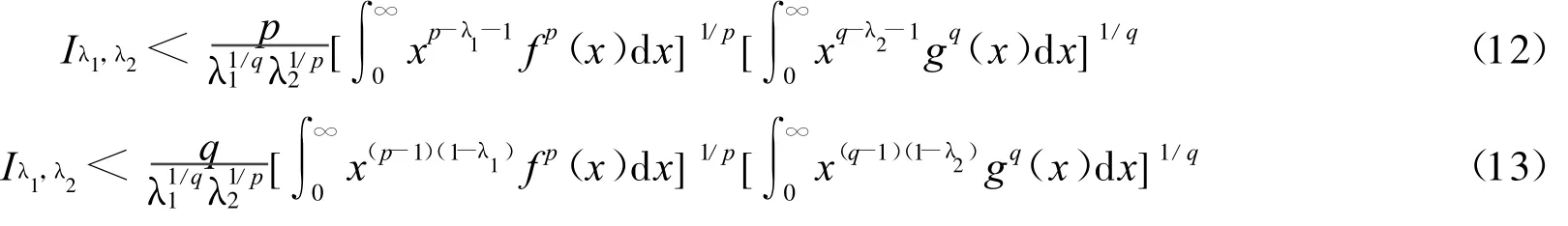
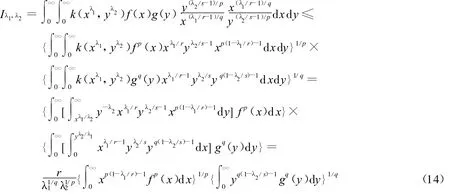
下面证明式(14)中间取严格不等号,若不然,必存在不全为0的常数A和B,使得:Afp(x)yλ2/s-1x(p-1)(1-λ1/r)=Bgq(y)xλ1/r-1y(q-1)(1-λ2/s)a.e 于(0,∞)×(0,∞)。即有 Axp(1-λ1/r)fp(x)=Byq(1-λ2/s)gq(y)a.e于(0,∞)×(0,∞)。于是有常数C,使 Axp(1-λ1/r)-1fp(x)=Cx-1a.e于(0,∞)。不妨设A ≠0,则可得 xp(1-λ1/r)-1fp(x)=,无论C是否为0,积分的结果必与相矛盾。于是 ,式(11)成立。

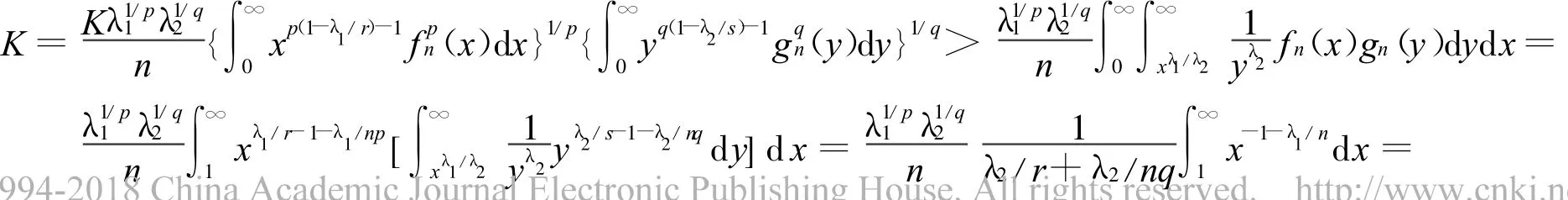
定理2 设λ1,λ2＞0,p＞1,r＞0(r≠1),1/p+1/q=1,1/r+1/s=1,f(x),g(x)为(0,∞)上的非负可测函数,且则有如下积分不等式:

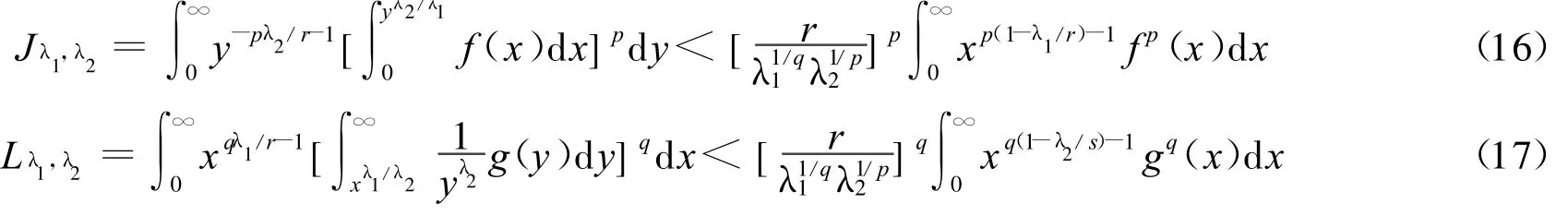
1)当r=p时,有如下与式(12)等价的不等式:

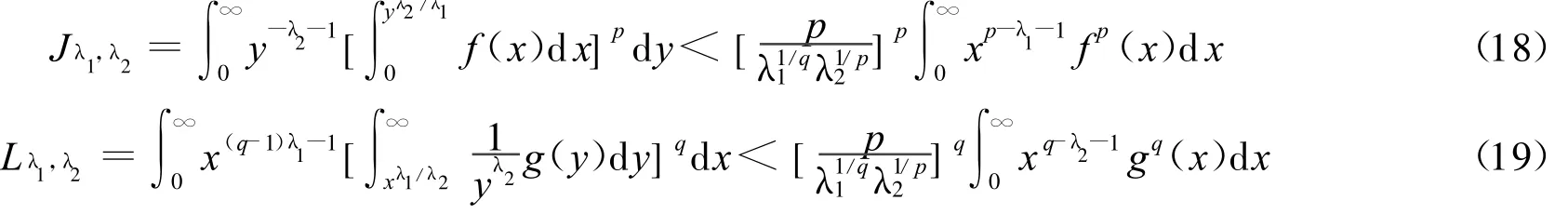
2)当r=q时,有如下与式(13)等价的不等式:

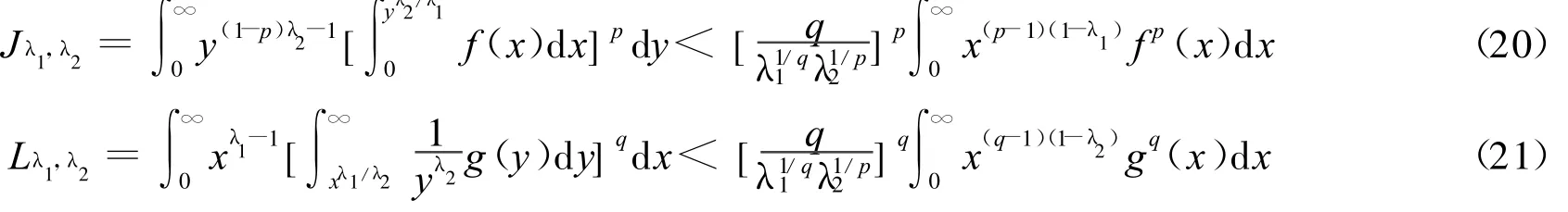
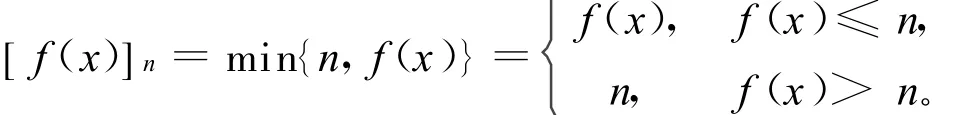
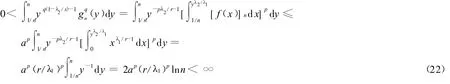
由式(11),当 x∉[1/n,n],gn(x)=[f(x)]n=0,因此有

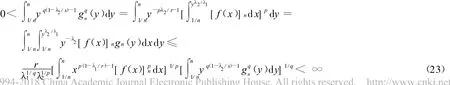
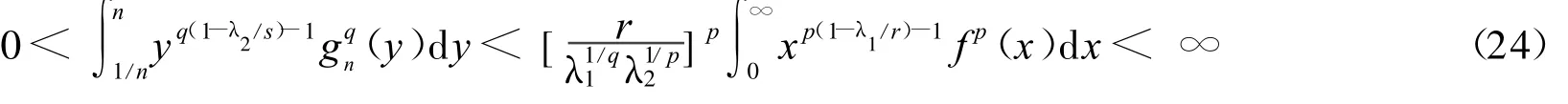
反之,设式(16)成立,由 Holder不等式,有

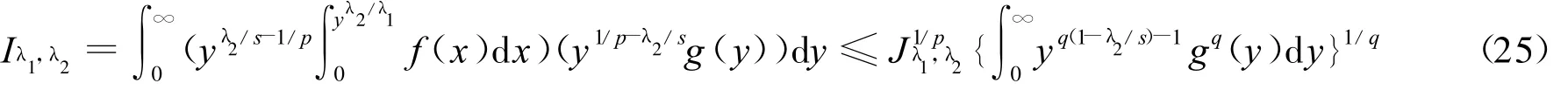
再由式(16)得式(11),因此式(16)和式(11)等价。

若式(11)的常数因子不是最佳值,则由式(25)易知式(11)的常数因子也不是最佳的,矛盾。

若在定理1、定理2的证明中,取r=1,并默认1/s=0,则有

推论1 设 λ1,λ2＞0,p＞1,1/p+1/q=1,f(x),g(x)为(0,∞)上的非负可测函数,且0＜则有如下积分不等式:

若在定理 1 、定理 2 的证明中 ,设 k(xλ1,yλ2)=1/yλ2,xλ1/λ2 ≥y;k(xλ1,yλ2)=0,xλ1/λ2 ＜ y 及r ＜0,则有如下定理:

定理3 设λ1,λ2＞0,p＞1,r＜0,1/p+1/q=1,1/r+1/s=1,f(x),g(x)为(0,∞)上的非负可测函数,且则有如下积分不等式:

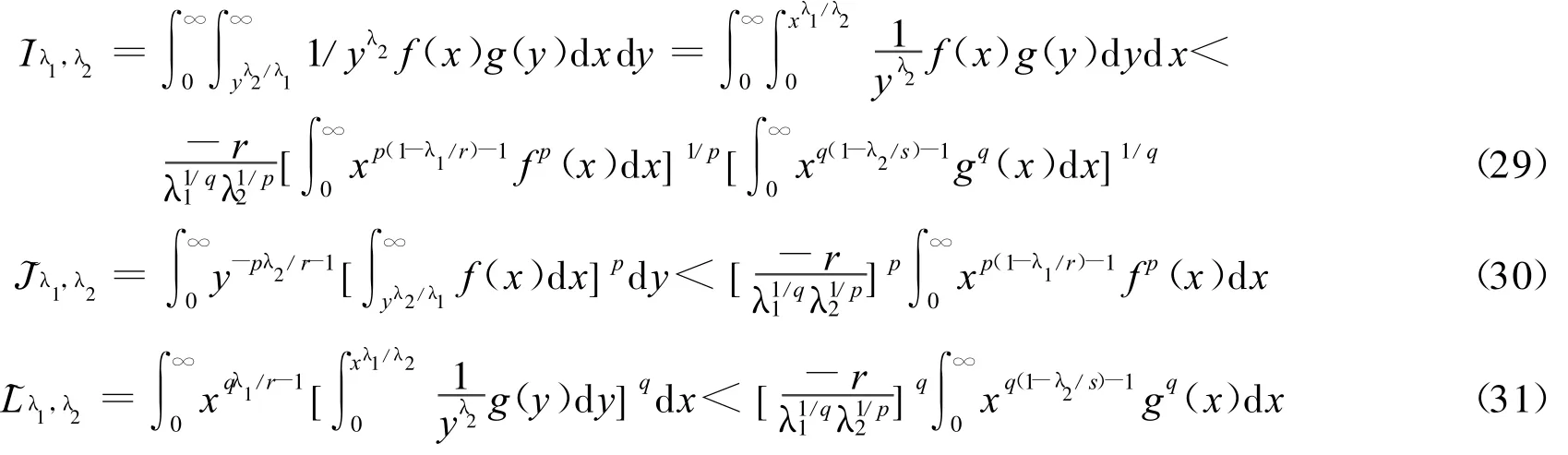
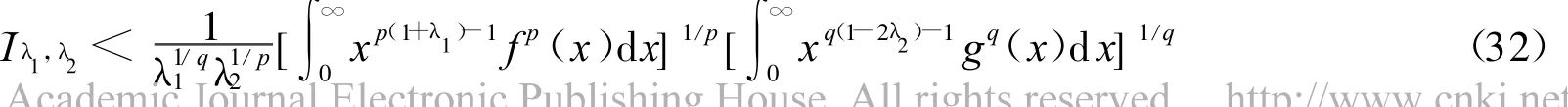
注 :1)当λ1=λ2=λ时,式(11)、(16)和(17)分别变为式(8)、(9)和(10);

2)当λ1=λ2=1时,式(20)和(21)分别变为式(4)和(5);式(18)和(19)分别变为如下等价不等式:

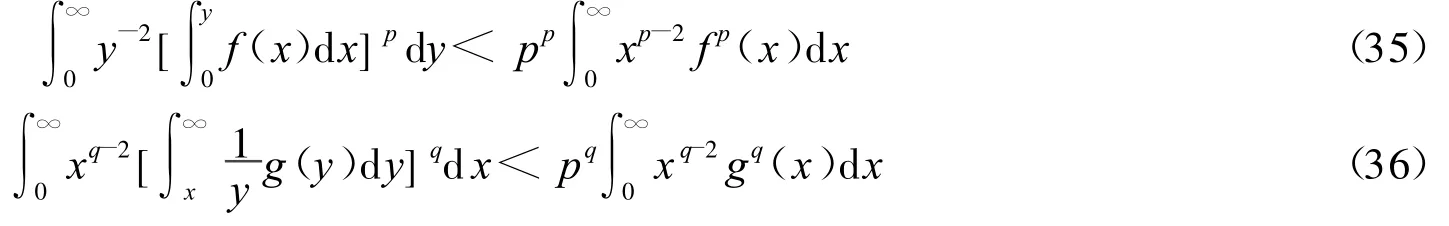
[1] HARDY G H,LITTLEWOOD JE,POLYA G.Inequalities[M].Cambridge:Cambridge University Press,1952.

[2] HARDT G H.Note on a theorem of hilbert concerning series of positive terms[J].Proc London Math Soc,1925,23(2):45-46.

[3] HARDY G H.Note on a theorem of Hilbert[J].Math Zeitschr,1920,6:314-317.

[4] MITRINOVIC D S,PECARIC J E,FINK A M.Inequalities Involving Functions and Their Integrals and Derivatives[M].Boston:Kluwer Academic Publishers,1991.

[5] YANG B C,BRNETI I,KRNI M,et al.Generalization of Hilbert and Hardy-Hilbert integral inequalities[J].Math Ineq Appl,2005,8(2):259-272.

[6] 和炳.关于Hilbert积分不等式的参量化推广[J].广东教育学院学报,2008,28(3):18-21.

[7] 杨必成.参量化的Hardy型积分不等式[J].上海大学学报:自然科学版,2010,16(4):404-408.

[8] 匡继昌.常用不等式[M].3版.济南:山东科学技术出版社,2004.