一类带粗糙核的多线性奇异积分交换子的CBMO估计
张慧慧,陶祥兴
1 引言及主要结果
设Sn-1为Rn上面的单位球面,带有通常的Lebesgue测度dσ=dσ(x′),并且满足如下消失性,

则具有粗糙核的奇异积分算子定义为
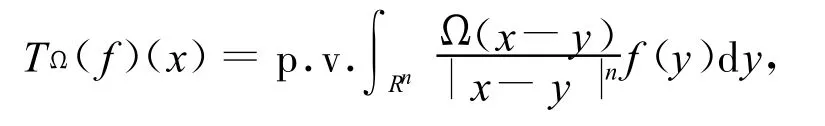
其中Ω∈Ls(Sn-1),(1≤s<∞),核函数Ω满足零次齐次性并且在单位球面上具有如式(1)形式的消失性。
对于上述算子TΩ,文献[1-2]对其进行了深入的研究。在此基础上,对每一个属于有界平均振荡空间的函数b(x),奇异积分交换子Tb(f)(x)的定义如下:
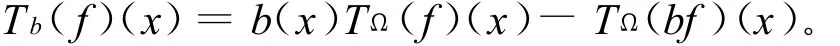
对于上述算子,Coifman等人于文献[3]中给出了一个经典的结论,即Tb(f)(x)为Lp(1<p<∞)有界的充要条件为b∈BMO,其中BMO为有界平均振荡空间。
1999年,Lu等人在文献[4]中定义了如下的中心有界平均振荡空间CBMO q,
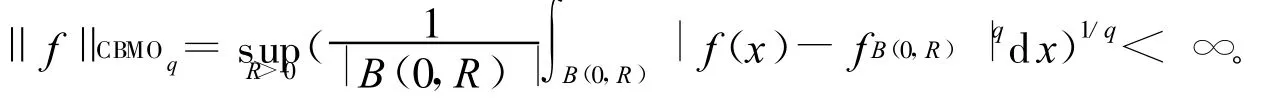
注意到BMO⊂CBMO q,因此当b∈CBMO q时,算子Tb(f)(x)的Lp(1<p<∞)有界性将不一定成立。
最近,Alvarez等人在文献[5]中定义了如下的λ-中心有界平均振荡空间CBMOq,λ(Rn)及 λ-中心Morrey 空间 Bq,λ(Rn)。
定义1[5]给定λ<1/n,1<q<∞,λ-中心有界平均振荡空间CBMOq,λ(Rn)定义为
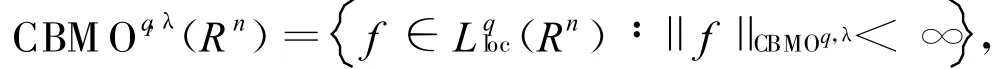
其中 ‖f‖CBMOq,λ范数定义为

定义2[5]令 λ∈ R,1<q<∞,则λ-中心Morrey空间Bq,λ(Rn)定义为

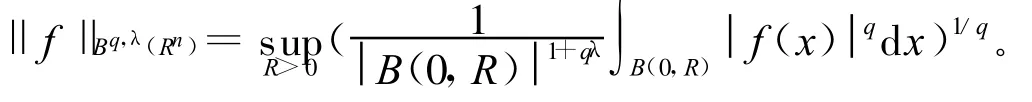
Alvarez等人证明了当b ∈ CBMOq,λ时,算子Tb(f)(x)在λ-中心Morrey空间Bq,λ(Rn)是有界的,其中核函数Ω(x)为有界函数。
对于核函数Ω∈Ls(Sn-1)的情形,2008年,Fu等人在文献[6]中证明了如果b∈CBMOq,λ,则相应的交换子 Tb(f)(x)也是在λ-中心Morrey空间Bq,λ(Rn)有界的。
同时,2002年,Perez等人在文献[7]中考虑了如下形式的多线性奇异积分算子交换子,

受上述工作启发,本文定义了一类带粗糙核的多线性奇异积分交换子。并在此基础上研究其在λ-中心Morrey空间上的有界性问题,得到了其在λ-中心Morrey空间中的CBMO估计。

本文的主要定理:
定理1 令TmΩ,b→(f)(x)为如上具有粗糙核的多线性奇异积分算子交换子,其中核函数Ω∈Ls(Sn-1),(1<s<∞)且在单位球面上满足一阶消失性,b→=(b1,b2,…,bm),bi∈ CBMOsi,μi(Rn),0<μi<1/n,1<si<∞,i=1,2,…,m。如果1<p<∞,/p <1,ν∈ R且上述指标满足+ν<0,则对任意 f ∈ Bp,ν,则有
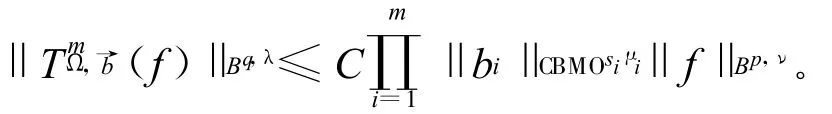
2 定理1的证明
在证明定理1之前,需要如下的引理。
引理1[1]设 TΩ(f)(x)为前所述的具有粗糙核的奇异积分,若1<q<∞,Ω∈Ls(Sn-1),(1<s<∞),且在单位球面上满足式(1),则有 ‖TΩ(f)‖Lq(Rn)≤C‖f‖Lq(Rn)。
定理1的证明 不失一般性,这里仅仅证明m=2的情况,m>2的情况完全类似。
固定一个常数R >0,定义B=B(0,R)及kB为B(0,kR)(k∈Z)。对 ∀x∈B,接下来可以对(f)(x)作如下的分解,
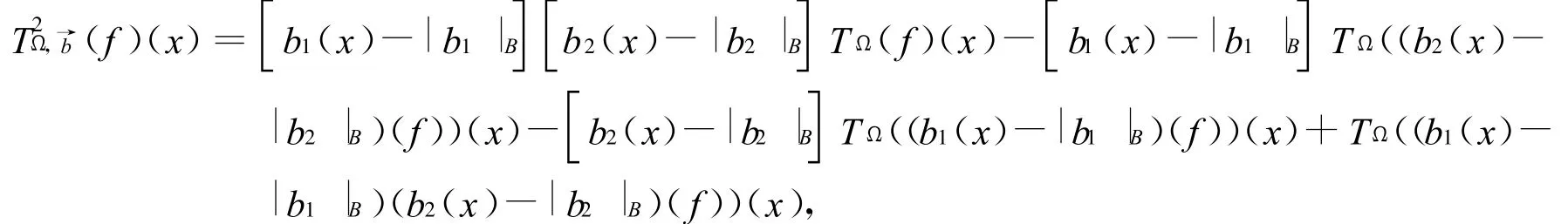

记 f=fχ2B+fχ(2B)c=∶f 1+f 2,其中χ2B为2B上面的特征函数。下面分别估计J 1,J 2,J3,J4。
1)J1部分
首先注意到
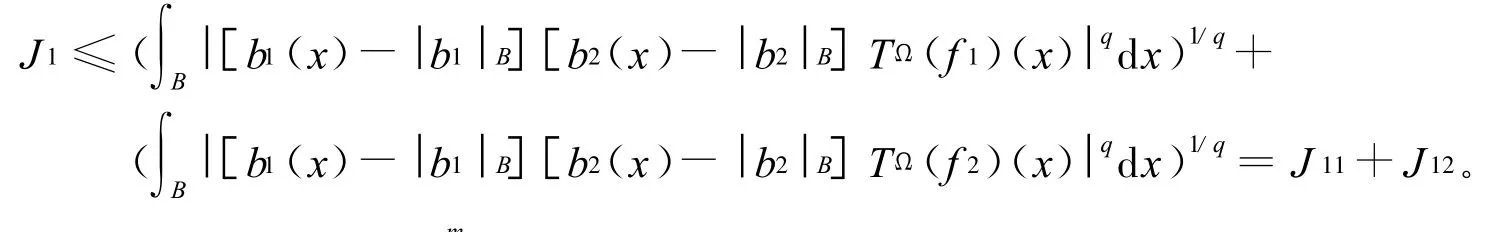

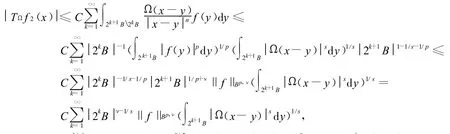
又由x∈B,y∈2k+1B可得x-y∈2k+2B,注意定理中的条件Ω∈Ls(Sn-1),从而有
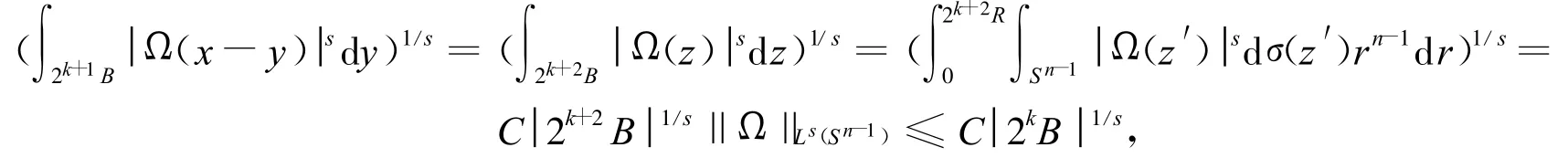
注意到ν<0,从而得到
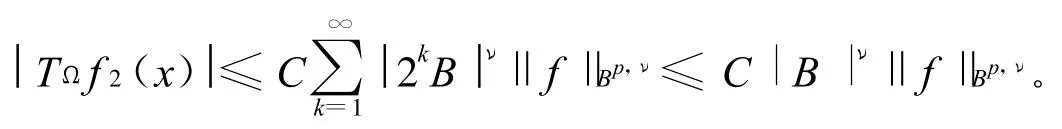
故由H¨older不等式可得
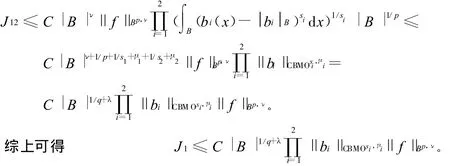
2)J4部分
首先由f的分解可得
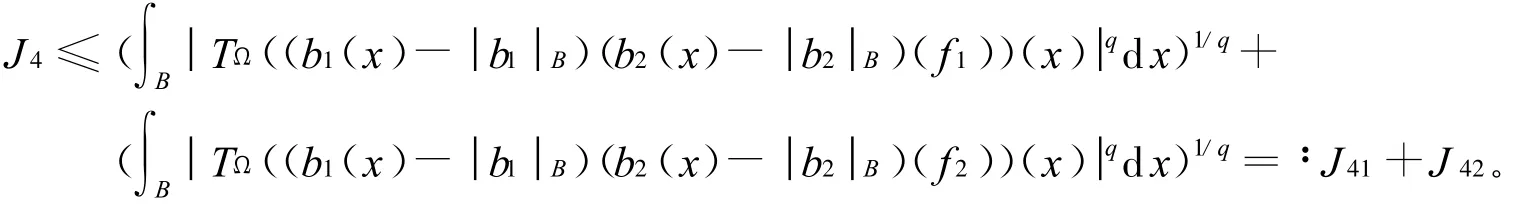
对于J41,根据,因此由算子 TΩ的 Lq(q>1)有界性和H¨older不等式得


综上可得
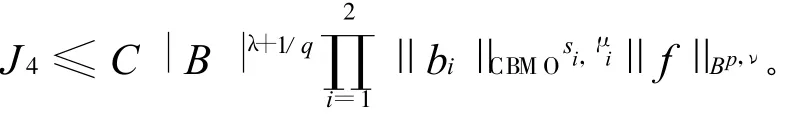
3)J2部分
记1/q1=1/q-1/s1=1/s2+1/p,则由H¨older不等式和 f的分解可得
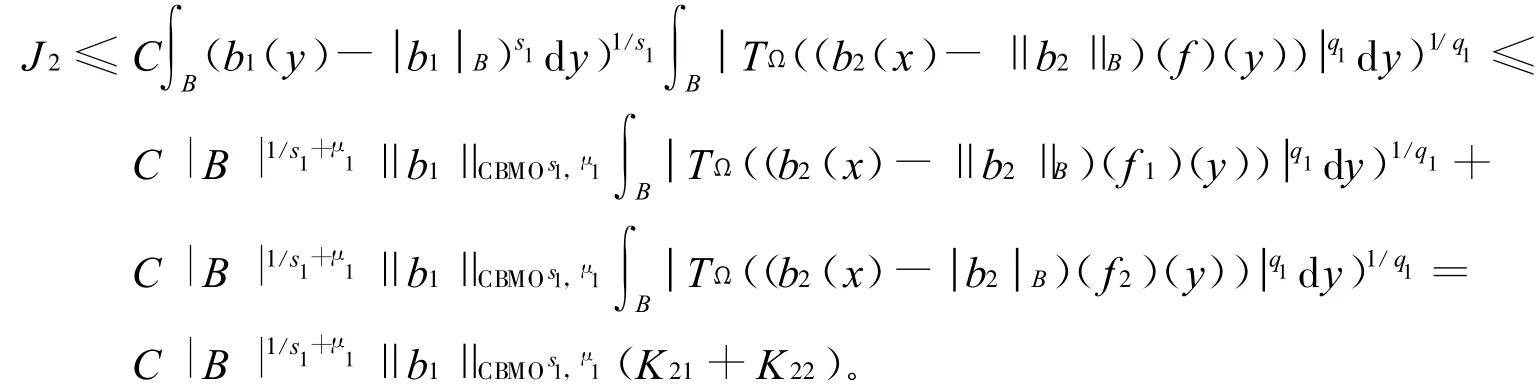
又类似于J41和J42的证明方法并且注意到1/q1=1/s2+1/p易得
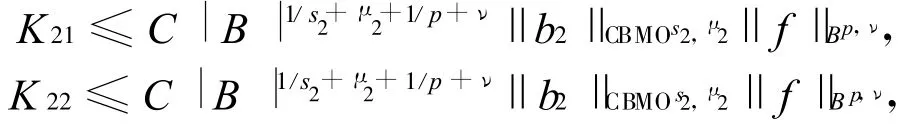
故有

4)J3部分
由于J3部分和J 2部分是对称的,因此类似于J 2的证明方法可得
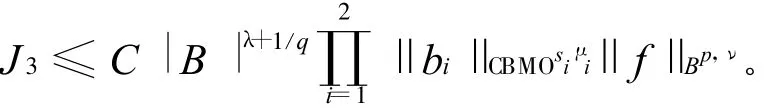
综合 1)、2)、3)、4)可得
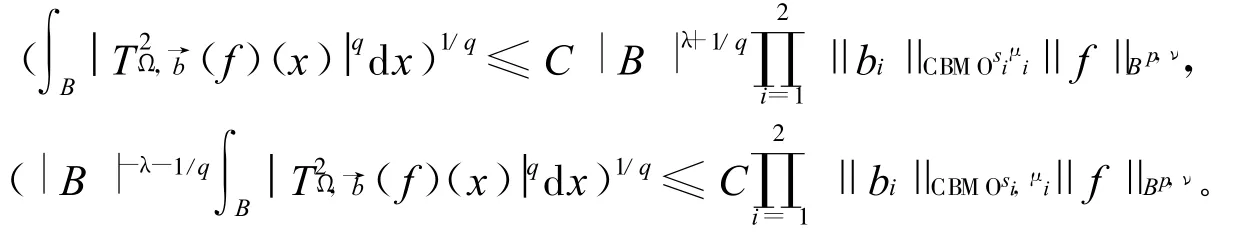
即
对上式两边取上确界,结合λ-中心Morrey空间相关定义,定理1得证。
[1] M UCKENHOUPT B,WHEEDEN R L.Weighted norm inequalities for singular and fractional integrals[J].Trans Amer Math Soc,1971(161):249-258.
[2] FAN D S,PAN Y B.Singular integrals with rough kernel operators supported by subvarieties[J].Amer JM ath,1997,119(4):799-839.
[3] COIFMAN R R,ROCHBERG R,WEISSG.Factorization theorems for Hardy spaces in several variables[J].Annals of Math,1976(103):611-635.
[4] LU SZ,YANG D C.Thecentral BMO spaces and Littlewood-Paley operators[J].Approx Theory Appl,1995,11(3):72-94.
[5] ALVAREZ J,LAKEY J,GUZMAN-PARTIDA M.Spaces of bounded λ-central mean oscilation,Morrey spaces,and λcentral Carleson measures[J].Collect Math,2000(51):1-47.
[6] FU Z W,LIN Y,LU S Z.λ-central BMO estimates for commutators of singular integrals with rough kernels[J].Acta Math Sinica(English Ser),2008(24):373-386.
[7] PEREZ C,TRUJILLO-GONZALEZ R.Sharp weighted estimates for multilinear commutators[J].J London Math Soc,2002,65(2):672-692.
[8] STEIN E M.Harmonic Analysis:Real Variable Methods,Orthogonality and Oscillatory Integrals[M].Princeton Univ Press,1993.
[9] TAO X X,SHI Y L.Multilinear commutators of Calderon-Zygmund operator onλ-central Morrey spaces[J].Adv Math,2011,40(1):47-59.

