某类高阶偏微分系统离散谱的估计
黄振明
(苏州市职业大学基础部,江苏苏州215104)
0 引言
包含拉普拉斯算子Δ的方程或方程组是数学和物理学中较常见的一类,有关它们的谱估计已取得了一系列成果[1-7].现作进一步的推广,考虑下面包含Δ的一类高阶偏微分系统谱估计问题:
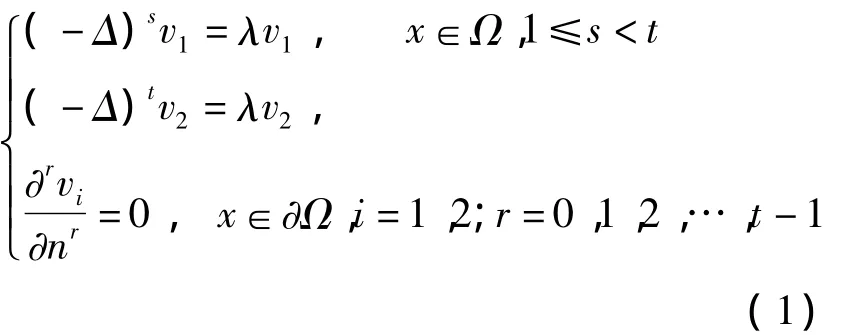
其中Ω⊂Rm(m≥2)是一个边界逐片光滑的区域,n是边界 ∂Ω的单位外法向量,x=(x1,x2,…,xm),s,t是任意的正整数.
笔者主要运用文献[1]中的方法,并且参照文献[2]对方程及文献[3]对算子的讨论方法,推广到对偏微分系统(1)的谱估计,获得了用前n个谱来估计第n+1个谱的上界的不等式,其估计系数与区域Ω的几何度量无关,文献[4]讨论的问题是式(1)中当s=1,t=2时的特例,文献[5]讨论的问题也是式(1)中当s=2,t=3时的特例,因此本文结论是文献[4-5]的进一步推广,在物理学和力学等领域中有一定的应用价值[8].
1 主要结果
定理 1 设 λi(i=1,2,…,n+1)是式(1)的谱,则:
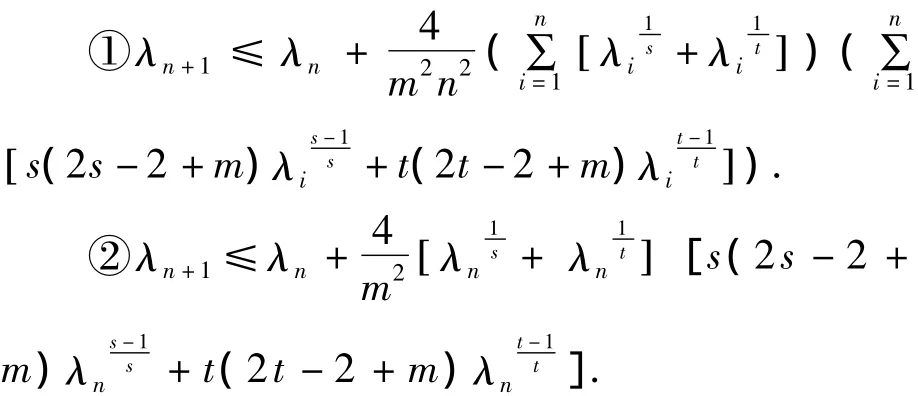
定理2 对于任何整数m≥2,n≥1,有:
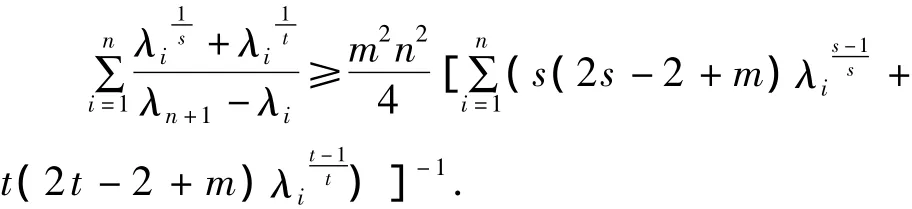
2 定理的证明
记▽·▽=▽2=Δ,2维函数列向量u=

设式(2)的谱为 0<λ1≤λ2≤…≤λn≤…,与之相对应的正交特征向量为(i=1,2,…,n),即满足:
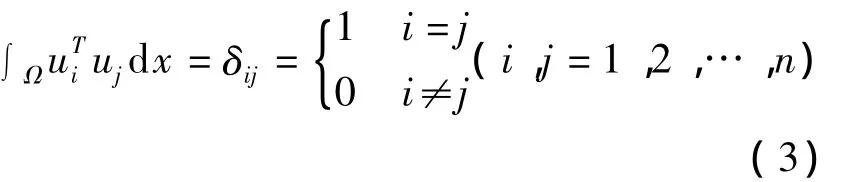
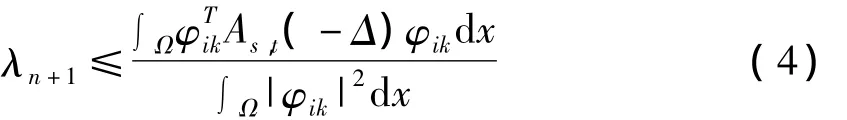
计算可得:
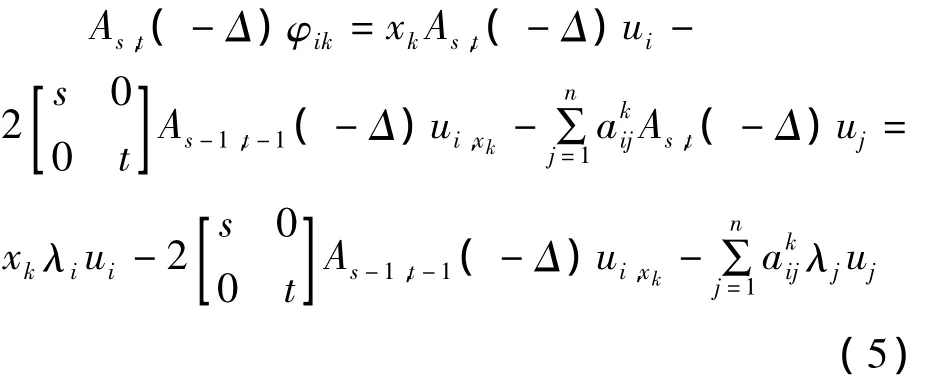
利用 φik与uj(j=1,2,…,n)的正交性,以及等式,从式(5)有:
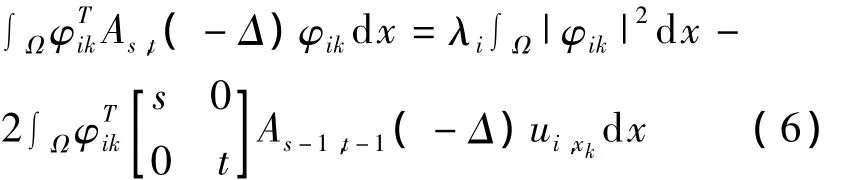

利用式(4)和式(7)有:
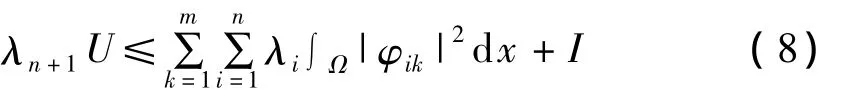
在式(8)中,用 λn替代所有的 λi(i=1,2,…,n),有:

引理1 设ui是式(2)对应谱 λi(i=1,2,…,n)的特征向量,则:
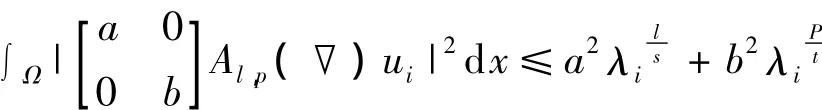
(a,b为实数)
证明 因为v1i,v2i分别是方程(-Δ)sy=λy和(-Δ)ty=λy对应的谱 λi的特征函数,由文献[3]中引理1可知:
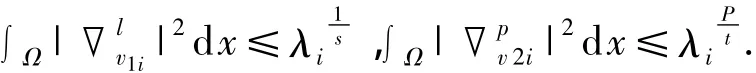
于是:
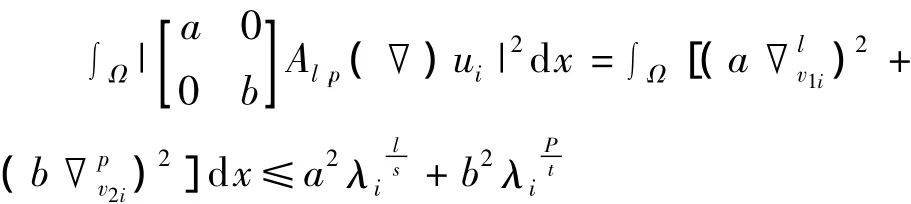
即得引理1.
引理2 设ui是式(2)对应谱 λi(i=1,2,…,n)的特征向量,则:

证明 ①利用分部积分,有:
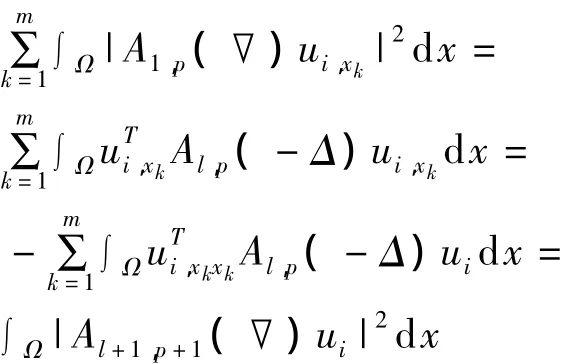
②类似地:
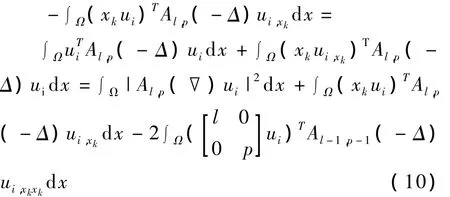
由式(10)可得:
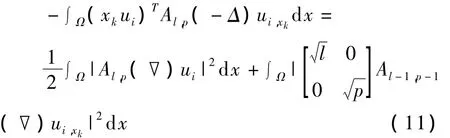
利用引理2①和式(11),有:
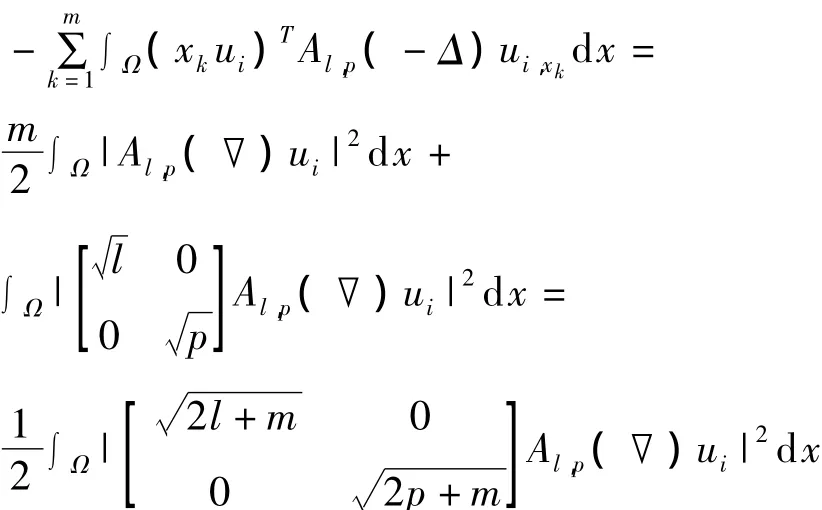
证毕.
引理 3 设 λ1,λ2,…,λn是式(2)的n个谱,则:
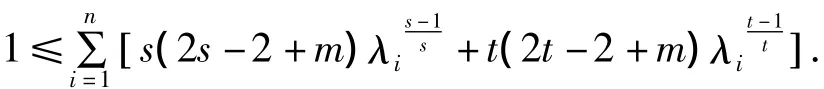
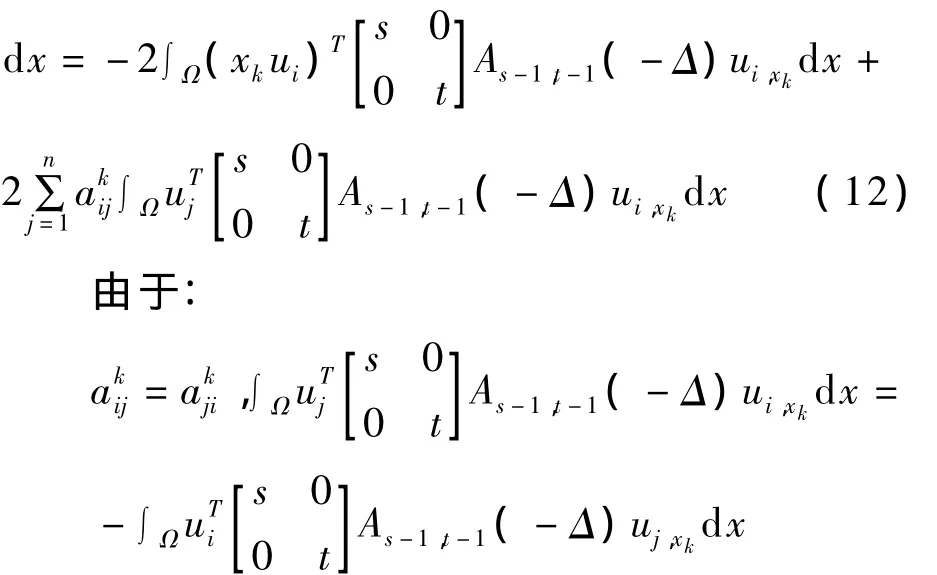
所以有:

利用引理2②,由式(12)知:
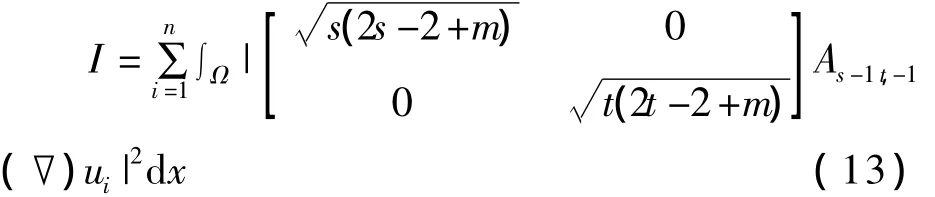
利用引理1和式(13)得:

证毕.
引理4 对于上述 φik和 λi(i=1,2,…,n,k=1,2,…,m),有下列不等式成立:
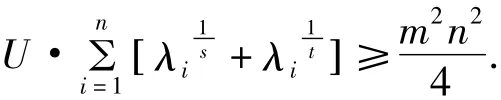
证明 由φik的定义,有:
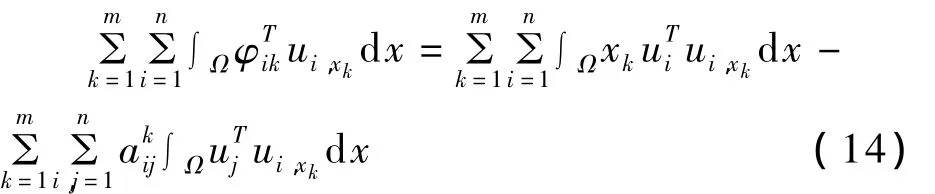
易知式(14)右端第 2项恒等于 0,又

利用式(14)、式(15)和式(3)得:
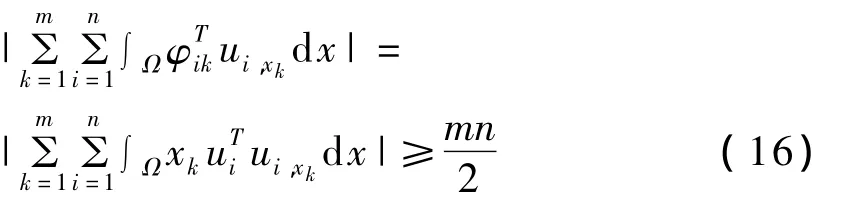
利用式(16)、Schwartz不等式和引理1(取a=b=p=l=1),有:
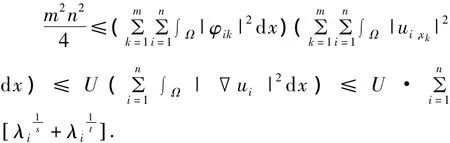
即得引理3.
定理1的证明:利用引理3和引理4,由式(9)可得定理1①,在定理1①右端用λn替代λi,可得定理 1②.
定理2的证明:选择参数 σ>λn,利用式(8),得:
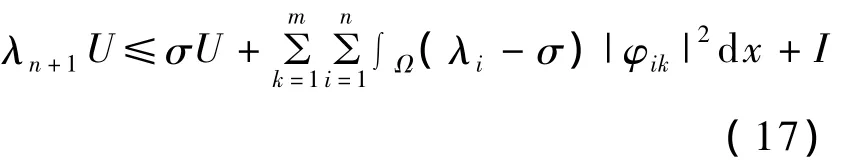
利用式(16)和Young不等式,有:

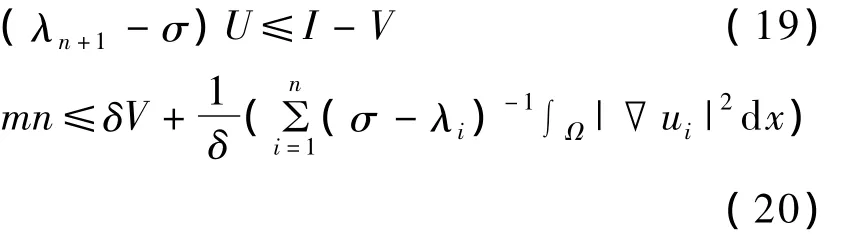
利用引理1和式(20),有:
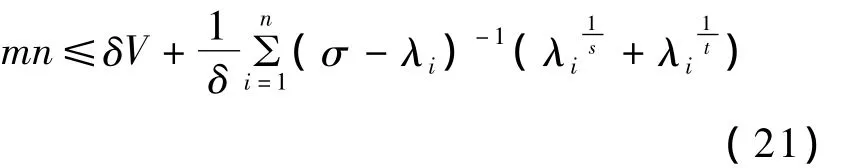
为了使式(21)右端的值达到最小,取δ=

利用式(21)和式(22),得:
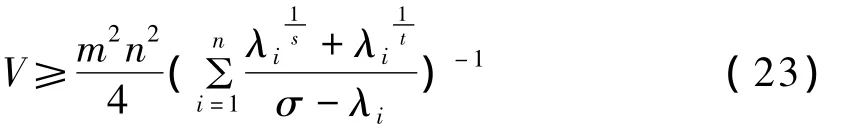
将式(23)代入式(19),得:
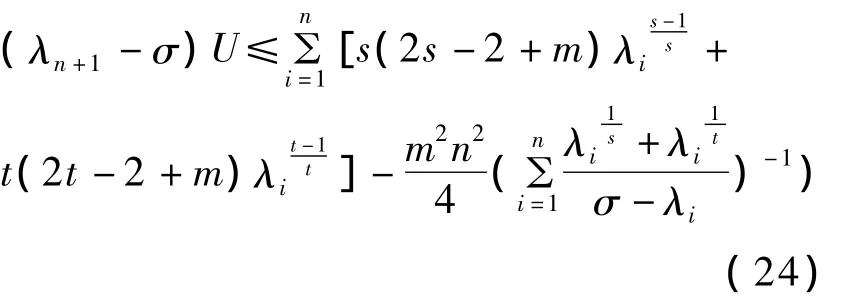
其中σ>λn,选取 σ,使不等式(24)右端等于0,即:
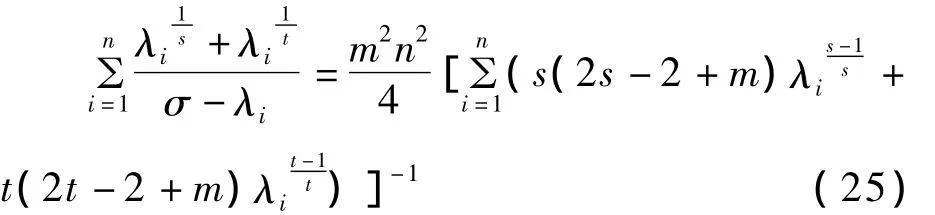
[1]Hile G H,Yen R Z.Inequalities for Eigenvalues of the Biharmonic Operator[J].Pacific J.Math,1984,112(1):115-133
[2]吴平.重调和方程特征值的上界估计[J].苏州铁道师院学报:自然科学版,2002,19(1):21-25
[3]黄振明.多项式算子谱的带权估计[J].南通大学学报:自然科学版,2006,17(2):20-23
[4]钱椿林,蒋麟.某类系统的离散谱估计[J].江苏广播电视大学学报,2000,11(4):1-3
[5]黄振明.一类偏微分系统的离散谱估计[J].苏州科技学院学报:自然科学版,2010,27(2):4-8
[6]陈祖墀,钱椿林.调和算子二次式的离散谱估计[J].应用数学学报,1989,12(3):368-373
[7]CHEN Z C,QIAN C L.Estimates for discrete spectrum of the Laplacian operator with any order[J].China Univ Sci Tech,1990,20(3):259-265
[8]Protter M H.Can one hear the shape of a drum?[J].SIAM Rev,1987,29(2):185-197

