基于正多面体法的单相异步电机优化设计

马吉祥 孙 华

（1.上海交通大学电子信息与电气工程学院，上海 200129；2.江苏省吴江市供电公司，江苏 吴江 215200）

单相异步电动机又称单相感应电动机，具有结构简单，价格低廉，运行可靠，维护使用方便等一系列优点，被广泛运用于轻工设备，日用机电器具等诸多方面，成为最贴近人们生活的电机品种。随着电力电子和控制技术的不断发展，单相异步电机的控制性能也得到了很大的提升，因此对其进行优化设计，降低其成本，提高其性能是必然的趋势。

传统电机优化设计[1-2]采用的优化算法是一种基于设计变量可微分性的数值方法，主要有直接搜索法和随机搜索法两种寻优模式，其中经典寻优策略有Powell法、单纯形法、惩罚函数法（SUMT）[3]、可变容差法和梯度法等等。20世纪90年代以来，模拟退火（SA）[4-8]、遗传算法（GA）[9-14]、禁忌搜索（TS）[15]和模拟进化（SE）等现代启发式优化算法得到迅速发展。其中惩罚函数法（SUMT）的惩罚因子常常难以选取；惩罚因子过大，函数会因对分配的权重过小而忽略对目标函数的影响，将给计算增加困难，惩罚因子过小，惩罚项得不到足够的惩罚，满足约束条件的精度就会降低。模拟退火算法（SA）的温度控制难以掌握，计算量很大，需要太长的计算时间，直接影响了此算法的寻优能力。遗传算法（GA）需要进行大量的目标特性的分析，如果目标分析方法比较耗时，计算量很大，此外在遗传操作中会产生大量的不可行解，对参数的控制要求也比较严格，且易发生早熟现象。

正多面体法是一种约束优化的有效方法，收敛迅速，在搜索过程中只需要计算目标函数值，程序简单，控制量少。算法包含平移、翻转、收缩3个主要动作，利用搜索点的局部测试信息来寻找目标函数的下降方向，并向这个方向平移，越限后翻转或者收缩，然后重复这样的动作直至到达最优点。正多面体法适合于单相异步机这样低成本，结构简单的电机设计，是本文研究的算法。

1 正多面体算法的基本原理

1）选择一个可行点（内点）X(0)作为初始点，在n维欧氏空间中生成一个以 X(0)为形心，边长为T0的初始正多面体。此正多面体具有n+1个顶点。

2）在比较形心点 X(0)和正多面体n+1个顶点的目标函数数值以及约束满足的情况下，使正多面体在n维空间执行平移，翻转和收缩等3种基本搜索策略，并形成一个新的正多面体。在每次变动中必须满足以下条件：

（1）在搜索过程中，始终保持形心在可行域D内。

（2）在搜索过程中，正多面体不发生畸变，始终保持为正多面体的形状，只是位置或大小有所变化。

（3）每次搜索变动后，正多面体形心的目标函数值必须小于变动前的形心函数值。

反复运用上述3种基本搜索策略，使新的正多面体的形心 X(0)逐渐逼近最优点X*。

3）以2维的正三角形为例加以说明。

（1）平移：每在一个新的正多面体形成后，经过形心函数值和各顶点函数值比较后，如果有一个函数值最小的可行顶点 X(L)，其函数值 FL比形心X(0)的函数值F0还要小时，正多面体就沿 X(0)X(L)连线方向平移搜索（如图1所示）。

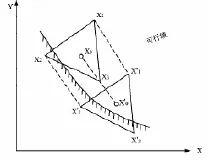
图1 平移策略

平移步长H就是形心 X(0)与那个好顶点 X(L)的距离，即

平移点为

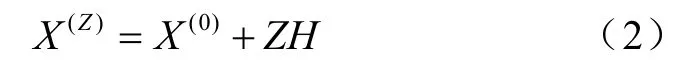
函数值为 F ( Z )= F( X(Z))，一旦平移成功，则按步长H继续平移，直至平移失败，退回最后一个成功点 X(Z)，且把 X(Z)作为新正多面体的形心 X(0)。

如果可行顶点 X(L)的函数值 FL并不比形心函数值F0小时，则无法平移，而进入翻转移动。若各顶点中无一是可行点，则进入收缩。

（2）翻转：当正多面体所有可行顶点的函数值均比形心值F0大时，就准备翻转。所谓翻转就是，除某一顶点 X(U)外，正多面体的其他几个定点不动，将 X(U)用其他n个顶点所决定的超平面对称点X(W)来代替，形成一个新的正多面体（如图2所示）。

图2 翻转策略

翻转后的新正多面体的形心 X(V)称为原正多面体的旁心。显然，一个正多面体有n+1个旁心，可以有n+1种不同的翻转。

为实现最理想的翻转，从n+1个旁心中找出函数值最小的可行旁心，记 X(V)，其函数值记为FL。如果满足

即旁心的函数值 FL小于原正多面体形心得函数值F0，则实施这种翻转，并令 X(0)= X(V)；否则，说明无法进行翻转，只能实现收缩。

（3）收缩：当正多面体的各顶点均为非可行点或无法进行翻转时，就实施收缩。将正多面体的各个顶点均向形心 X(0)收缩相同的距离，本文中收缩1/2，使形成的新正多面体的边长T也相应收缩1/2，即

如图3所示。

2 正多面体法的具体实现

（1）给定维数n，初始可行形心 X(0)，初始边长 T0和精度ε。 T0要取得适当，如果取得过大或者过小都会增加搜索时间。

图3 收缩策略

（2）形成初始正多面体：设形心 X(0)的坐标为函数值为 F0= F ( X(0))则n+1个顶点坐标可用两维数组 X Y( i, j)表示如下，行号i为顶点号，列号j为该顶点的各维坐标分量。

其中

（3）判别正多面体的各个顶点是否均为外点。

如果所有顶点都为非可行点，则转式（9）进行收缩；否则转式（4）。

（4）找出可行域中的最好顶点 X(L)

若满足 F L＜F0，则转式（5）进行平移；否则转式（6）找旁心。

（5）平移搜索：平移的方向是 X(0)→X(L)，平移的步长为 H = X(L)- X(0)。对 Z=1，2，…，n，依次考察 X(Z)= X(0)+ ( Z + 1 )H ， F ( Z )= F ( X(Z))。如果X(Z)是内点，且 F ( Z)＜F0，即平移成功，继续平移，且令 Z = Z+1， F0= F ( Z)；否则，退回最后一个成功点作为形心，即

平移后形成的新正多面体的各顶点坐标为

且转式（3）。（6）计算各旁心，并判别是否均为外点？各旁心的坐标为

各旁心的约束函数最大值

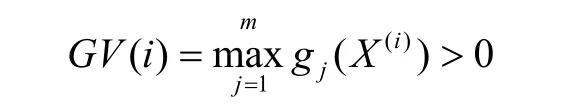
若各旁心均为非可行点，则转式（9）进行收缩；否则找出最好的可行旁心 X(V)，其函数值记为FL。

（7）翻转判别：如果满足 F L＜F0，则转式（8）实施正多面体的翻转，否则式（9）进行收缩。

（8）翻转计算：设翻转前的形心为 X(0)，顶点为 X(U)，翻转后的对应顶点为 X(W)，翻转后的新形心为 X(V)，则

且转式（3）

（9）收缩：当形成的正多面体的各顶点均为非可行点或者无法进行翻转移动时，便实施收缩策略。将正多面体各顶点向形心 X(0)移动一半的距离，形成一个新的小正多面体。各新顶点的坐标为

(i = 1 ,2,… ,n + 1 , j = 1,2,… ,n )边长也减为一半，即

（10）终止迭代判别：如果正多面体的边长满足

此时，则输出最优点

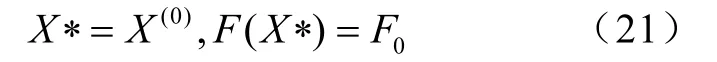
否则转式（3）进行新的迭代。

3 软件开发和算例分析

3.1 软件的主要功能

（1）根据电机结构和尺寸计算其电磁特性、输出转矩、效率、输出功率等力能指标以及温升、损耗和有效材料成本。

（2）采用基于正多面体算法，以成本作为目标函数对电机的结构参数进行优化，并进行优化前后电机性能和成本的比较。

3.2 软件的主题结构

根据软件的主要功能，可分为两个模块，即电机电磁特性、性能、成本等计算模块和优化算法模块。模块图如图4所示。

图4 软件模块图

3.3 算例分析

我们以有效材料成本为目标函数，采用正多面体优化算法对单相异步电机进行了优化设计。这里我们采用的电机仍为单相4极异步电机，额定转速1500r/min，额定功率14W，电压200V。具体结果如表1所示。

表1 参数对比分析

优化后，主绕组槽满率下降了29.02%，副绕组槽满率下降了27.38%，成本降低了6.73%。

4 结论

（1）正多面体算法程序简单，控制量少，在搜索过程中只需要计算目标函数值，避免了因进行大量的目标特性分析、方法比较而造成的速度慢，计算量大，运算时间长等弊端。

（2）正多面体算法具有收敛迅速的优点，操作过程中不会产生大量的不可行解。

（3）正多面体算法适用于低成本，结构简单的电机设计，可有效地降低成本，具有经济实用性。

[1]俞鑫昌,电机、电器优化设计[M].机械工业出版社,1988.

[2]王充权,电机的计算机辅助设计与优化技术[M],上海:上海交通大学出版社,1989.

[3]Martin D W.Tee 1-1 J. Iterative methods for linear equations with symmetric positive definite matrices[J].The Computer Journal. 1961-1962(4).

[4]孟大伟,张弘,基于模拟退火算法及直接搜素法的混合优化策略在电机设计中的应用[J].电机与控制学报,1997, 1(2): 92-94.

[5]满春涛,黄金杰,张筱磊,基于模拟退火算法的模糊控制器优化设计[J].电机与控制学报,2004,8(3): 281-284.

[6]Xi Ziqing and Zhou Keding. An improved simulated annealing algorithm and its application in global optimization of structure of a transformer core [C].Proc. of ICEF’2000,Tianjing 2000,322-324.

[7]Wang Youhua, Yan Weili et al. Adaptive simulated annealing for the optimal design of electromagnetic devices[J]. IEEE Trans. On Magnetics,1996, 32(3):1214-1217.

[8]Annakkage U D, Numnonda T,Pahalawaththa N C. Unit commitment by parallel simulated anneailng[J]. IEE Porc-Gener,Transm..Distrib,1995, 142(6):595-600.

[9]Cao Y J, Wu Q H. Optimal reactive power dispatch using an adaptive genetic algorithm[C]. Glasgow, UK:in Proceedings of Int. Conf. on Geneitc Algorithm in Engineeirng Systems,1997,117-122.

[10]Gomes J R, Saaverdra O R. Optimal reactive power planning using evolutionary Computation: Extended Algorithm[J].IEE Gen. Trans. and Dis,1999,146(6):586-592.

[11]张俊礼,葛斌,遗传算法在压水堆核电机组给水回热分配中的应用[J],中国电机工程学报,2005,25(6):152-156.

[12]GARRET I H, LA IN . A knowledge-based system for designing transformers and inductors[C].IEEE Conference Proceedings, The 4th Conference. on Artificial Intelligence Application,1992.

[13]王育槐,吴建华,杨仕友,倪光正,多目标矢量优化的改进遗传算法及其在电磁装置优化设计中的应用[J],中国电机工程学报,2004,24(7):215-218.

[14]David C Walters,Gerald B Sheble. Genetic algorithm solution of economic dispatch with valve point loading[J].IEEE Trans on PS,1993,8(3): 1325-1332.

[15]杨仕友,倪光正,钱金很,电机电磁场逆问厄数值计算的改进Taba算法[J],中国电机工程学报,1998,18(4):83-86.