基于隶属函数-G1法的变压器状态综合评判
王菲菲 罗日成 刘从法 吴 莹 蒋 琼
(长沙理工大学电气与信息工程学院,长沙 410014)
长期以来,变压器的运行状况都是通过定期维修来判断,这种“到期必修”的维修方式,容易出现“过修”和“欠修”状态。因此,在电力系统高可靠性和经济性的迫切要求下,状态维修取代定期维修已成为电力变压器维修方式的必然发展趋势。对变压器的运行状态进行合理评价是状态维修的重要依据。
目前,变压器的状态评价受到国内外很多学者的关注。文献[3]提出了 0-100分的评分机制,考虑了静态分值和动态分值两个指标,但评分中使用简单的比值法不利于对未来检测数据的准确判断。文献[5]应用证据理论对特征量进行融合,但没有考虑到各个证据体之间的相互关联,降低了评价结果的准确度。文献[8]采用灰靶理论进行评估,提高了评价的可信度和准确性,但由于AHP确定权重计算量大,数据量大时难以达到一致性。
针对上述问题,考虑到变压器状态信息的多层次性、多因素性,分别采用 G1法和隶属度函数法计算内涵性权重和结构性权重,利用组合赋权法将变压器状态各指标有机结合在一起,使得变压器状态评估信息间权重的分配更加合理、客观。然后建立了两级综合评判模型实现了变压器状态的分层多级综合评判。
1 待评价各分项指标的确立
通过对变压器各项信息分析,掌握了其真实情况后,将变压器状态分2级评价,提出变压器状态待评价各分项指标,如表1所示。

表1 待评价各分项指标
2 变压器状态信息综合权重的确定
2.1 用G1法确定各指标的内涵性权重
1)用G1法确定指标的序关系[1]
2)专家给出相邻指标 Xk-1与 Xk重要性程度之比 rk的理性赋值, rk= Xk-1Xk。rk首先由各个专家独自判定,然后取其平均值。对于指标数量较大时,可以取最次要指标 rm= 1 。其中,rk的取值可以参考表2。

表2 比例标度及含义
3)若专家给出了 rk的理性赋值,则准则层下第m个指标对该准则层的G1法权重ωm,1为
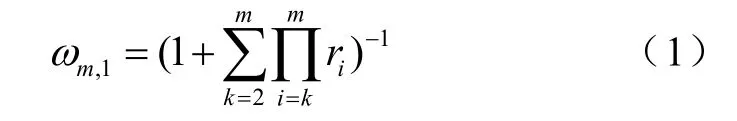
4)由权重ωm,1可得第m-1,m-2,…,3,2个指标的权重计算公式为
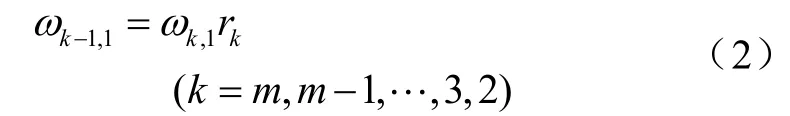
ω1=为各指标的内涵性权重向量。
2.2 用隶属函数法确定各指标的结构性权重

2)定义各指标的结构性权重为

由(4)式可知,对于某一指标,当 λi=0时,ωi,2=1,而其他指标的权重则为0。
2.3 综合权重的确定

内涵性权重反映了专家的经验,不能反映指标的变化,权数确定后不会变动;结构性权重指标的权数与指标值密切相关,随着指标的变化而变动。通过(5)式的组合赋权,使得专家的经验和指标的实际情况有机结合起来,进而实现了权重在各指标间的合理分配。
3 模糊综合评判
如表1所示,变压器状态待评价各分项指标共13项,分为3类,因此我们先对每一类进行综合评判,将其结果看成是一个单因素评判,而这三类指标看成三个因素并赋予权重 A,进行第二级综合评判[4]。
1)一级综合评判模型
通过计算各类指标的隶属度,可得到如下模糊综合评价矩阵:
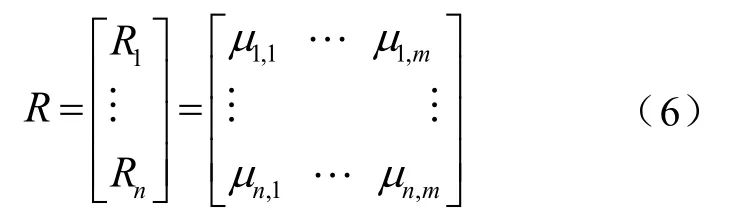
式中,n为指标数;m为质量等级数; Ri为第 i项指标的单因素评价。
将μij进行归一化处理:
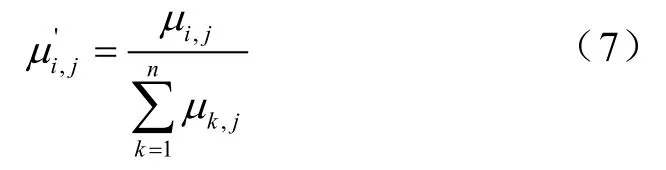
评价结果为

其中,ω为综合权重矢量,B为模糊综合评价结果向量。
2)二级综合评判模型

其中, Bi是第i类指标评判的结果,而C是类之间的综合评判结果。
4 实例应用分析
下面根据某 220kV主变的一次预防性试验记录、运行中绝缘油特性技术资料[2]对其运行状态进行评判。
部分预试数据:工频交流耐压绝缘电阻 8000 MΩ(32℃时),吸收比1.5(没有做极化指数试验);泄露电流22μA;主变本体介损值为0.33%(32℃时);直流电阻不平衡系数为0.9%(30℃时)。
经过整理后绝缘油试验数据见表3所示。
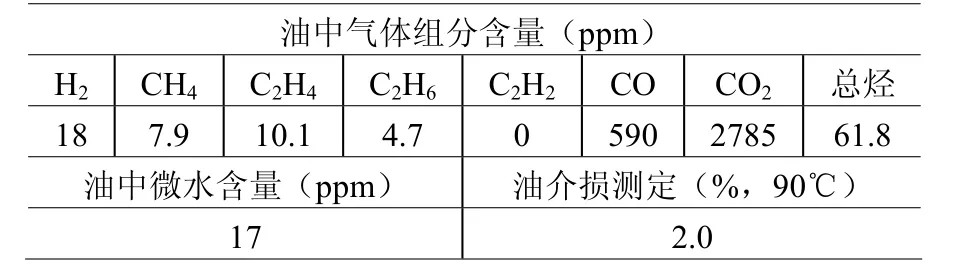
表3 绝缘油试验数据
计算步骤如下:
第一步以变压器一级评价为例,根据 G1法综合一些专家的意见,对评价指标建立如下序关系:试验项目>运行工况>检修指标。
第二步各个专家独自判定然后取其平均值,确定指标之间的相对重要程度: r2= 1 .8, r3= 1 .6。
第三步根据式(1)、式(2)可得


ωi,1为步骤一所确定的序关系所对应的指标内涵性权重,如ω1,1为试验项目的内涵性权重。即一级指标的内涵性加权向量为 ω1= ( 0.5255,0.2920,0.1825)。
第四步同理,可求得变压器状态二级指标的内涵性加权向量,分别为

第五步本文中将变压器状态统一划分为:良好状态、较好状态、一般状态和注意状态,并建立单个指标对这四种状态的隶属度函数,最终求得试验项目、检修指标和运行工况的评判矩阵。

采用隶属函数法[2]对该变压器的试验项目二级指标数据进行分析,可得试验项目二级指标结构性加权向量为

同理

第六步根据式(5)可得待评价二级指标的综合权重向量

第七步将该变压器各项试验数据代入隶属度函数,可以得到相应的隶属度。对二级指标隶属度数列用步骤六所得到的权重向量进行加权平均后可得到相应的二级指标隶属度。采用隶属函数法对变压器状态二级指标隶属度分析可得到一级指标结构性加权向量ω2为

第八步根据式(5)可得变压器状态一级指标综合权重向量
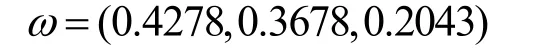
第九步将步骤5得到的评判矩阵和步骤6、8得到的综合权重向量代入式(8)和式(9),可分别求得一级评判结果和二级评判结果。评判结果分别为

第十步对综合评判结果进行加权处理,用1,2,3,4分别代表良好状态、较好状态、一般状态和注意状态,对评判结果进行加权平均得 V = 1 .8169。V介于1和2之间,更接近于2,所以该变压器的整体状态介于“良好状态”和“较好状态”之间,且更接近于“较好状态”。同理,对一级评判结果进行加权处理后,可得 V1= 1 .8007, V2= 1 .9117,V3= 1 .6809。可见 V1, V2, V3均介于1和2之间且更接近于 2,所以分别从试验项目、检修指标、运行工况方面可以看出此变压器运行状态较好。这与文献[2]的判断结果是一致的,且更接近实际情况,对状态检修现场具有重要的指导意义。
5 结论
由以上计算结果看出,该方法不仅考虑了专家的主观权重,解决了AHP判断矩阵一致性检验的问题,而且确定了各指标间的动态权重,得出了比较科学的权重系数。针对变压器信息繁多和复杂的特点,建立了两级综合评判模型。该方法将相关状态参量有机的结合起来,对变压器运行状态的正确评估作出了积极的探索,对变压器的故障诊断和状态检修现场实践具有重要的指导意义。该方法投入工程实际后,经检验具有准确实用、计算结果明确、易于推广等特点,基本适应目前变压器状态评价水平和要求。
[1]迟国泰,祝志川,张玉玲.基于熵权-G1法的科技评价模型及实证研究[J].科学学研究,2008,26(6):12-13.
[2]王谦.基于模糊理论的电力变压器运行状态综合评估方法研究[D].重庆:重庆大学,2005:43-54.
[3]WANG M, VANDERMAAR A J, SRIVASTAVA K D.Review of Condition Assessment of Power Transformers in Service[J]. IEEE Electrical Insulation Magazine,2002, 18(6):12-25.
[4]杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,2001:144.
[5]TANG W H, SPURGROR K, WU Q H, et al. An Evidential Reasoning Approach to Transformer Condition Assessments[J]. IEEE Transactions on Power Delivery,2004,19(4):1696-1731.
[6]刘有为,李光范,高克利等.制订《电气设备状态维修导则》的原理框架[J].电网技术,2003,27(6):64-67,76.
[7]李连结,姚建刚,龙立波等.组合赋权法在电能质量模糊综合评价中的应用[J].电力系统自动化,2007,31(4):56-60.
[8]郑玲峰,王建元,白志亮等.用改进的灰靶理论评价变压器状态[J].中国电力,2011,44(1):28-29.
[9]Yann-Chang Huang, Hong-Tzer Yang, Ching-Lien Huang. Developing a new transformer fault diagnosis system through evolutionary fuzzy logic[J]. IEEE Transactions on Power Delivery,1997,12(2):761-767.
[10]杜林,袁蕾,熊浩等.电力变压器运行状态可拓层次评估[J].高电压技术,2011,37(4):897-902.
[11]吴建锋,刘卓明.基于综合权重的变压器状态评估[J].广东电力,2009,22(9):9-10.
[12]Agou S, et al. Increasing the reliability of online insulation condition assessment of MV-HV equipment[J]. Electricity Today,2000,12(6):22-27.
[13]Qian Z, Yan Y. Fuzzy synthetic method for life assessment of power transformer[J].IEE Proc-Sci Meas Technol,2004,151(3):175-180.
[14]贾卫军.基于组合赋权的变压器状态模糊综合评估模型及其专家系统[D].北京:华北电力大学,2009:20-21.

