一种新型转速调节器在交流调速系统中的应用研究
吴冠平 林荣文 喻 晓
(福州大学电气工程与自动化学院,福州 350108)
随着电力电子器件和微电子技术的发展,自从磁场定向矢量控制技术和直接转矩控制(DTC)技术诞生以后,交流调速系统已广泛应用于现代高性能调速领域。在交流调速系统中对速度要求较高的场合一般都采用经典的比例积分(PI)调节器对速度进行闭环控制,PI调节器有良好的动态和静态性能,但在负载突变情况下速度会出现超调,一旦应用在需要频繁起、制动的场合,太大速度超调将严重影响控制效果甚至损坏机械设备,虽然可以调节PI控制器参数来消除超调,但会降低系统动态响应性能。而采用新型控制器,即可消除超调,又能使得系统具有较高的抗干扰能力,同时还能提高系统的响应时间。
本文先对交流调速系统进行简要分析,再对PI和新型控制器进行理论分析,并在 Matlab/simulink下构建了异步电动机直接转矩控制和永磁同步电动机矢量控制模型,分别对新型转速调节器与常规PI转速调节器的控制性能进行了对比分析,验证了新型速度控制器可进一步提高系统的抗干扰能力和动态响应能力。
1 交流调速系统
调速即转矩控制,是指在传动系统运行中人为或者自动地改变电动机的转速,以满足工作机械对不同转速的要求。电动机调速的任务是控制转速,转速通过转矩来改变,从给定电机转速到实际电机转速的闭环控制框如图1所示,其中 Go( s)为转速调节器的传递函数。

图1 闭环调速系统转速闭环框图
根据电机动力学可知道从转矩到转速是一个积分环节—机械惯量,即

式中, G D2为电动机和负载机械的飞轮转矩,n为转速, Te、 TL为电动机的电磁转矩和负载转矩。从上式看出,如果能快速准确地控制转矩,电机转矩实际值 Te与给定值 Te*之间是一个时间常数σT的惯性系统,则其传递函数为

转速通过转矩来改变,转矩不只和电流有关,还与磁链有关,电动机的转速、转矩和磁链耦合在一起,要实现高性能调速必须解开耦合,实现转矩和磁链的分别控制。变频调速的控制策略有两类:按电机稳态模型控制的调速系统和高效能控制系统,高性能调速通过控制定子电压电流矢量(幅值和相角)来分别控制转矩和磁链,从而控制转速,它主要有两种:矢量控制和直接转矩控制。
1.1 矢量控制系统
20世纪70年代西门子工程师F.Blaschke首先提出异步电机矢量控制理论来解决交流电机转矩控制问题。其基本思想是根据坐标变换理论将交流电机两个在时间相位上正交的交流分量,转换为空间上正交的两个直流分量,从而把交流电机定子电流分解成励磁分量和转矩分量两个独立的直流控制量,分别实现对电机磁通和转矩的控制,然后再通过坐标变换将两个独立的直流控制量还原为交流时变量来控制交流电机,从而实现了像直流电机那样独立控制磁通和转矩的目的,提高了调速的动态性能。图2给出了永磁同步电动机矢量控制框图,此矢量控制系统采用转速、电流双闭环系统,对永磁电机三相电流进行坐标转换,得到转矩电流和励磁电流,并与给定电流比较后经过调节器调节生成两相定子坐标系矢量电压,系统利用空间电压矢量确定逆变器的开关状态。
1.2 直接转矩控制
1985年德国鲁尔大学的狄普布洛克(M.Depenbrock)教授首先提出了基于六边形乃至圆形磁链轨迹的直接转矩控制理论,三相异步电动机直接转矩控制系统中定子磁链轨迹可以控制为六边形也可以是圆形。
图3给出了按定子磁链控制的异步电动机直接转矩控制系统的原理框图,此控制系统是分别控制异步电动机的转速和磁链,转矩和磁链的控制采用双位式砰一砰控制器,并在 PWM逆变器中直接用这两个控制信号产生电压的SVPWM波形,从而避开了将定子电流分解成转矩和磁链分量,省去了旋转变换和电流控制,简化了控制器的结构。转速调节器ASR的输出作为电磁转矩的给定信号 Te*,在Te后面设置转矩控制内环,它可以抑制磁链变化对转速子系统的影响,从而使转速和磁链子系统实现了近似的解藕。

图2 永磁同步电动机矢量控制原理图
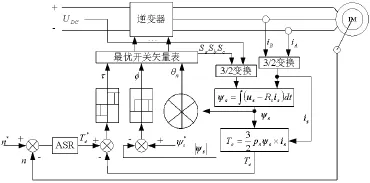
图3 异步电动机直接转矩控制原理图
2 转速调节器
从上面分析可知,调速的任务是控制转速,但调速的关键是转矩控制,高性能交流调速系统解决的就是转矩控制问题,所有调速系统的转速调节部分都一样,在图1中,从给定电机转速到实际电机转速的闭环控制系统开环传递函数
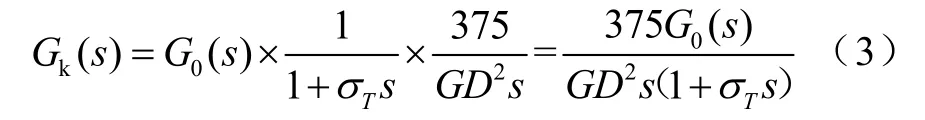
其闭环传递函数

Go( s)为转速调节器的传递函数,现在根据不同的控制策略进行确定。
2.1 PI转速调节器
PI控制器包含比例和积分两部分(如图 4所示),其中积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。因此PI控制器具有良好的动态和静态性能,并且可以通过极点配置改善系统的稳定性。如上图虚线框内所示,其中n、n*分别为实际速度、给定速度,Kp为比例增益, K1为积分增益。

图4 PI控制器原理图
则PI调节器的传递函数

采用 PI控制器作为转速调节器时控制系统的闭环传递函数为

从上式中可看出 PI控制器闭环控制时引入了零点 Kps + KI,在阶跃信号作用下,其比例和积分项同时作用,会引起较大超调,影响系统的稳定。
2.2 新型转速调节器
新型转速调节器原理图如图5所示,就是将传统 PI控制器中的比例控制环节由前向通道移到反馈通道,经过结构的改变,形成一种新型控制器。采用新型控制器作为转速调节器时闭环传递函数

从上式可以看出新型转速调节器控制系统闭环传递函数中没有零点,同时也增加了阻尼比,故新型转速调节器能明显的降低超调,但对瞬态响应提高不太明显。由于比例环节移到反馈通道中,从而形成反馈补偿,可有效提高系统的瞬态响应。若给定的速度发生阶跃变化,由于比例与积分的共同作用于速度误差,PI调节器的输出会快速变化,出现较大的超调。而在新型转速调节器中,只对速度误差起积分作用,而它的比例环节只对速度信号起作用并起到反馈补偿的作用,从而不会出现输出突变。同样,对于负载突变,新型转速调节器也能快速响应且超调量小,显出强抗干扰的能力,新型转速调节器的这些特点将在下面的实验仿真中得到验证。

图5 新型转速调节器原理图
3 Matlab/Simulink建模仿真
Matlab是当今流行的科学计算和仿真软件,具有强大的矩阵运算能力。Matlab提供的Simulink是一个用来对动态系统进行建模、仿真和分析的功能强大的软件包。Simulink具有友好的用户开发界面、开放的编程环境,用户可以开发自己的模型。根据上面给出的永磁同步电动机矢量控制原理图和异步电动机直接转矩控制原理图分别建立控制系统,其中ASR分别采用PI控制器和新型控制器。
3.1 永磁同步电动机矢量控制系统仿真结果
选用永磁同步电机参数:定子电阻 Rs= 2.875Ω,直、交轴的等效电感 Lq= Ld= 0 .0085H转子磁链ψf= 0 .175Wb,转动惯量J=0.0008kg·m2,粘滞系数B=0,极对数 pn=2,在此基础上仿真分析矢量控制系统的性能指标以及各因素的影响。在仿真过程中,t=0.2s时,负载转矩由1N·m突加到5N·m,在t=0.4s时,转速由 600r/min突变为 1200r/min。仿真得到分别采用 PI控制器和新型控制器作为转速调节器时永磁同步电动机矢量控制系统的转速和转矩的仿真图(如图6、图7所示)。

图6 两种不同转速控制器下转速仿真图

图7 两种不同转速控制器下转矩仿真图
3.2 异步电动机直接转矩控制系统仿真结果
选用异步电动机参数:额定功率 PN= 3730W ,定子电阻 Rs=1.115Ω,转子电阻 Rr=1.083Ω,转子电感 Lr=0.005974H,定子电感 Ls=0.005974H,定转子互感 Lm=0.2037H,极对数 pn=2,在此基础上仿真分析异步电动机直接转矩控制系统的性能指标以及各因素的影响。此模型建立一个运动轨迹近似为圆形的定子磁链,磁链给定值为 1.5Wb。仿真过程中,起动时负载转矩为20N·m,速度设为1000r/min,在t=1s时,负载转矩突加到5N·m,在t=2s时,转速突变到500r/min。仿真得到分别采用PI控制器和新型控制器做为转速调节器时异步电动机直接转矩控制系统的转速和转矩的仿真图(如图8、图9所示)。
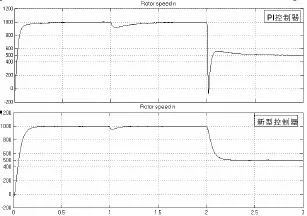
图8 采用不同转速控制器时转速仿真图

图9 采用不同转速控制器时转矩仿真图
3.3 仿真结果分析
上面给出了两个系统分别采用不同控制器作为转矩调节器的仿真波形图,从转速仿真图(如图6、图 8所示)中,我们可以看出,相对于采用 PI转速控制器,在负载发生突变时,采用新型控制器的转速恢复时间特别快,速度变化幅度非常小;在转速突变时,转速响应也很迅速,速度变化平稳,稳定性好。在转矩仿真图(如图7、图9所示)中,我们可以看出,相对于采用PI转速控制器,在负载和转速发生突变时,采用新型控制器时系统的转矩振荡幅度小,且能迅速响应。可见,新型转速调节器的控制性能优于PI转速调节器的,尤其表现在给定负载突变时新型转矩控制器控制时转速在极小波动后快速地达到稳定,进一步说明采用新型控制器时控制系统有更好的稳定性和抗扰动性能。
4 结论
本文对交流调速控制系统和转速PI调节器、新型转速调节器做了简要分析,并在Matlab/Simulink中构建的异步电动机直接转矩控制和永磁同步电动机矢量控制系统模型下分别采用转速 PI调节器和新型转速调节器进行仿真,通过仿真结果对比,易知,采用新型转速调节器时交流调速系统具有更好稳定性和抗干扰能力、动态响应能力。
[1]周扬忠,胡育文.交流电动机直接转矩控制[M].北京:机械工业出版社, 2010.
[2]马小亮.高性能变频调速及其典型控制系统[M].北京:机械工业出版社, 2010.
[3]姚俊,马松辉.SIMULINK建模与仿真[M].西安:西安电子科技大学出版社,2002.
[4]陈伯时.电力拖动自动控制系统.第二版.北京:机械工业出版社,2005.
[5]王洋,刘永光.基于 Smiulink的永磁同步电机矢量控制系统仿真.组合机床与自动化加工技术,2011 (2):78-82.

