基于两级Hough变换的机载雷达建航方法

段芳芳 王 伟 韩 星 张 明

(西安电子工程研究所 西安 710100)

1 引言

强地杂波环境下快速、准确的航迹起始是机载雷达数据处理的一个难点，并且由于载机的非直线运动、处理过程中的近似误差、大气扰动等一系列因素［2］，导致机载雷达测得的目标方位角在运动补偿后仍存在误差，使得正确航迹起始的难度进一步加大。目前常用的航迹起始方法［3，5，6］有基于逻辑的航迹起始方法、Hough变换法以及多假设航迹起始法。基于逻辑的航迹起始方法在大量地物杂波的密集多目标情况下，对判断规则要求苛刻，易引发较高的虚警率或漏警率;Hough变换法在密集杂波环境下，通常需要多次的扫描才能较好地航迹起始，因此不利于航迹的快速起始;多假设航迹起始法在理论上是最优的，但是其算法复杂，占用资源大，限制了它在工程中的使用。本文针对机载雷达目标特点，从工程实现背景出发，提出一种基于运动状态的两级Hough变换法。通过仿真和试验数据分析，证明该方法在保证航迹快速起始的前提下，可以有效降低虚假航迹起始概率。

2 原理简介

2.1 基于运动状态的Hough变换法［1，4］

在强地杂波环境下，目标的运动状态信息比位置信息更能反映目标航迹的特征，所以如果用目标状态信息对备选航迹进行检验，不但会极大地提高正确航迹起始概率，而且会减少虚假航迹起始概率。在Hough变换中，如果选取位移——时间作为参量，则匀速运动目标的问题转变为直线检测，其斜率反映目标的运动状态。假设候选航迹l的N次扫描中得到的量测为{(ri，θi)，i=1，2，…，N}，其中ri为第i次斜距量测值，θi为第i次方位角量测值，对其进行坐标转换得到两维笛卡儿坐标系中的量测值{(xi，yi)，i=1，2，…，N}。

对相邻的两次量测做如下变换:

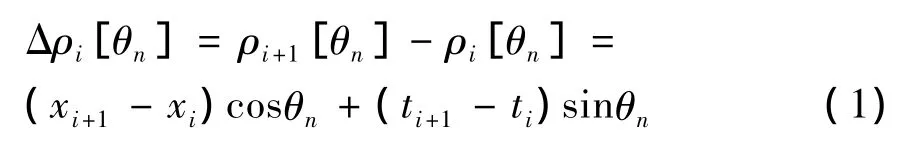
其中

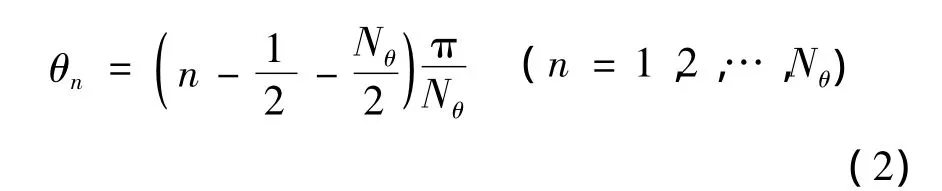
式中Nθ为参数θ的分割段数。

对于来源于同一航迹的量测，在短时间内由于其运动状态相同，所以总能找到θn=θ0(n=1，2，…，Nθ)，使得 Δρi［θn］=0，此时:

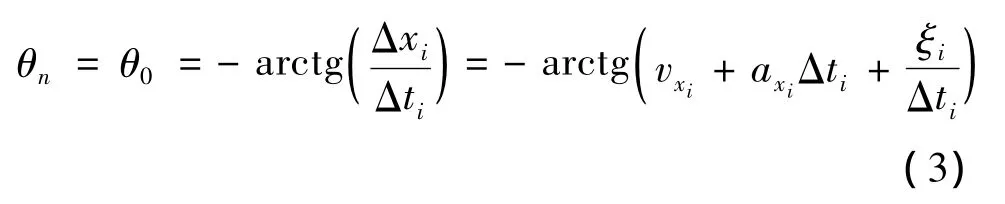
式中，i=1，2，…，N-1;Δxi=xi+1-xi是两次量测的x坐标之差，Δti=ti+1-ti是两次量测的时间差，ξi为量测高斯白噪声。由式(3)可以看出，对于来源于同一目标的量测，在短时间内应具有相同的运动状态，即目标的速度vxi、加速度axi不变。因此由公式(3)得到的θn应保持不变。图1中的实线为目标的运动状态vx+axΔti和θn(θ0)的关系，可以看出在θn∈［-50°，50°］时，线性度较好。为了使提取的目标运动状态有良好的线性和对应关系，可以根据目标运动状态的先验信息，对Hough进行修正，修正Hough为:

其中k=(vmax+amaxT)/12为比例系数，vmax和amax分别为目标的最大速度和最大加速度，T为采样周期。图1中虚线为利用修正Hough得出的目标运动状态和 θn(θ0)关系图，其中

2.2 基于运动状态的两级Hough变换法

在实际使用中，按照2.1节的方法对xi和yi分别做Hough变换，由于方位角误差的存在，xi和yi都受到方位角的影响。该影响导致，如果航迹起始波门选择过小则大多数航迹都不能起始，而过大则会产生很多虚假航迹。针对该问题，本文提出两级Hough变换的概念，即在基于运动状态的Hough变换后单独再做一级斜距的Hough变换，原理如下。

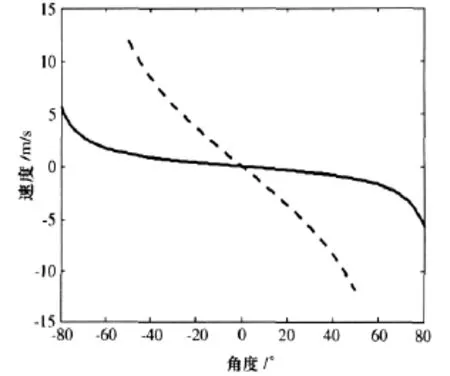
图1 运动状态和角度关系图

2.2.1 第一级Hough变换

先对xi和yi做基于运动状态的Hough变换。

选用稍大的波门δx和δy做粗筛选，去掉一部分航迹。即如果航迹满足和，则认为该航迹可能为可靠航迹，如果不满足，则该航迹为虚假航迹，直接从备选航迹中删除。

2.2.2 第二级Hough变换

由于在大于1km处，斜距ri与时间ti基本成线性关系，因此可以对斜距 ri做基于运动状态的Hough变换，用精细的波门δr做限制，得到最终的要起始的航迹。

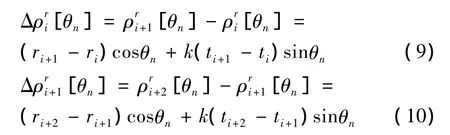
3 实现步骤

基于运动状态的两级Hough变换法的实现步骤如下:

a.为第一个雷达扫描帧接收到的每一个量测建航，作为备选航迹;

b.对于每一个备选航迹，如果超过一个以上的量测位于相关波门内，则利用简化的全局最近邻法则，找到此备选航迹的点;如果没有量测位于确认区域内，则此备选航迹进行一步外推;

c.当备选航迹有三个量测时，利用基于运动状态的两级Hough变换进行起始判定;

d.如上过程持续到第n个雷达扫描帧(一般n选为5～7)，如果备选航迹都能满足起始条件，且也满足n个雷达扫描帧中有m次观测，即符合m/n起始规则，则该航迹成功起始。

4 仿真试验

机载雷达监视区域为斜距2～20km，方位-45°～+45°。设虚警在整个监视区域内服从均匀分布，在目标跟踪门内虚警出现概率服从泊松分布，虚警概率密度为λ=4×10-4/m2。雷达扫描帧周期为1s。m/n逻辑法中 m=3，n=5，Hough变换中波门为 δx=δy=10°，δr=5°。模拟目标为 2 架飞机和 3辆车。2架飞机的飞行速度分别为v1=150m/s和v2=180m/s，起始位置分别为［r1，θ1］=［2500m，-5°］和［r2，θ2］=［3500m，1°］。3 辆车的行驶速度分别为 v3=50m/s，v4=80m/s，v5=70m/s，起始位置分别为［r3，θ3］=［10000m，0°］，［r4，θ4］=［5000m，12°］，［r5，θ5］=［3000m，5°］。

引入评价指标:

其中N为Monte-Carlo仿真试验次数，fi为在第i次仿真中起始的虚假航迹数;ni为在第i次仿真中起始的航迹总数。

其中lit代表第i次仿真试验中目标航迹t是否被正确起始。

表1为m/n逻辑法、基于运动状态的Hough变换法和本文提出的基于运动状态的两级Hough变换航迹起始方法的仿真结果比较。

表1 三种航迹起始方法仿真结果对比

从三种航迹起始方法的仿真结果可以看出，本文提出的方法在正确航迹起始概率和起始时间两项指标与m/n逻辑法和基于运动状态的Hough变换法相当，而虚假航迹起始概率明显降低。

5 试验结果

在某型号机载雷达航迹起始的试验中，进行6次试验，每次试验约300个雷达扫描帧的数据，试验中有两架飞机作为合作目标，飞机的下方是一条四车道的公路，路上车辆为非合作目标。试验结果见表2，其中作为合作目标的两架飞机的航迹起始概率均为100%。

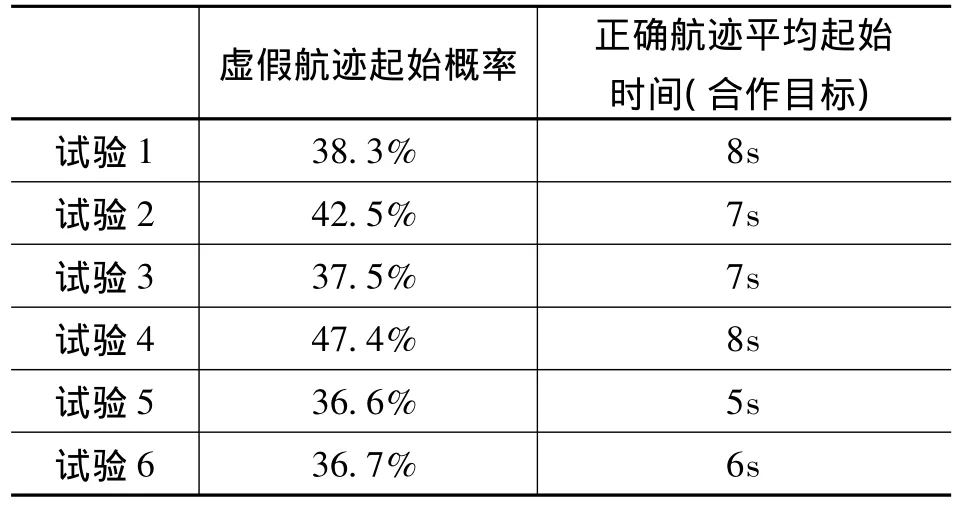
表2 试验结果

从试验结果可以看出，本文提出的方法在实际使用中虚假航迹起始概率较低，航迹起始时间满足系统要求，该方法有效可行。

6 结论

本文针对机载雷达下视目标的特点，提出了一种基于运动状态的两级Hough变换航迹起始方法。经过Monte-Carlo仿真分析和试验数据证明，该方法在保证航迹快速起始的前提下有效降低了虚假航迹起始概率。

［1］Hu Z.J.，Leung H.Statistical performance analysis of track initiation techniques［J］.IEEE Trans.on AES(S0018-9251)，1997，45(2):445-456.

［2］George Stimson.机载雷达导论［M］.吴汉平等译.北京:电子工业出版社，2005.

［3］朱自谦.并行联合概率航迹起始逻辑［J］.电子学报，2007，35(12):2421-2424.

［4］汤琦，黄建国，杨旭东.航迹起始算法及性能仿真［J］.系统仿真学报，2007，19(11):149-152.

［5］朱洪艳，韩崇昭，韩红，左东广.航迹起始算法研究［J］.航空学报，2004，25(3):284-288.

［6］王国宏，苏峰，毛士艺，何友.杂波环境下基于Hough变换和逻辑的快速航迹起始算法［J］.系统仿真学报，2002，14(7):874-876.