涡旋式水源热泵系统性能仿真

(上海交通大学机械与动力工程学院 上海 200240)

传统涡旋式水源热泵的设计需要进行大量的实验，耗费巨大且设计周期长，而利用数学模型对系统性能进行仿真，并在此基础上进行性能分析和优化，则将大大缩短设计周期并节省设计费用。目前，计算机仿真技术已应用于小型制冷装置[1]和大型螺杆冷水机组[2]的优化设计。而对以涡旋式水源热泵为代表的中型热泵，其关键部件涡旋压缩机和电子膨胀阀的大规模商业运用限于近十多年，因此对于其模型和系统算法方面的研究还不够成熟。

压缩机模型方面，兼顾速度与精度的半经验压缩机模型[3-5]在系统仿真中被优先考虑。但现有的半经验模型在某些方面未尽完善，如未考虑吸气加热过程对工质流量的影响[3]，需要较多的实验数据来确定模型参数[4]以及不能预测排气温度[5]等。电子膨胀阀的建模方面，反映电子膨胀阀动态控制特性的模型大多较为复杂，影响计算的速度和稳定性[6]；若忽略电子膨胀阀对过热度的控制，从而将之简单地作为节流短管来处理[7]，则又会因为无法反映阀的开度的影响而导致精度不够，且开度值难以确定。系统算法大致可归纳为三种，即连续迭代法[8]、顺序模块法[9]和方程联立求解法[10]。连续迭代法在迭代变量较多的情况下收敛性难以保证，但在处理小规模问题时速度快且稳定。后两者虽然都存在速度较慢、健壮性较差的问题，但适于处理中大规模问题，尤其是顺序模块法通过模块化提高了模型的易维护性。因此设计系统算法时可综合各种算法的优点。

以下将建立适用于系统仿真的涡旋式热泵系统模型，为了保证系统模型的稳定性和易维护性，将结合顺序模块法和连续迭代法对模型进行求解。

1 系统模型

系统模型由压缩机、换热器以及节流装置等子模型构成。

1.1 涡旋压缩机模型

系统仿真计算中，压缩机模型需要输出工质流量、输入功率和排气温度这三个参数，而输入参数则为吸气温度和压力、排气压力、环境温度以及压缩机的结构参数。

气体在涡旋压缩腔中压缩结束时(点3)的压力p3取决于涡旋压缩腔内容积比εv，如果出现过压缩或欠压缩时，气体将会在压缩腔排气口进行一个等容过程直到压力等于排气压力pdis(点4)。因此，压缩机输入功率Pin可以表示为式(1):

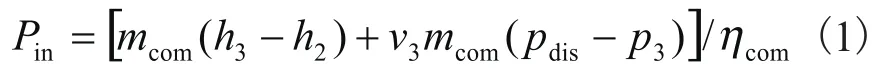
式中:v3—压缩终了比容，v3= v2/εv。

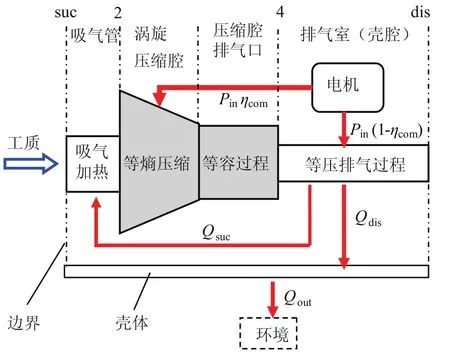
图1 涡旋压缩机压缩过程能量流动图Fig.1 Working process energy flow of scroll compressor

如图1所示，涡旋压缩腔排出的高温气体在壳体内与壳体以及电机换热，并且加热吸气管中的吸气，从而温度降低[8]。吸气过程模型如式(2)所示，排气过程模型如式(3)和(4)所示。由于壳体会与环境换热，而输入功率耗损被机体吸收，为了反映该关系还需要补充压缩机能量平衡方程与流量方程，分别如式(5)和(6)所示。

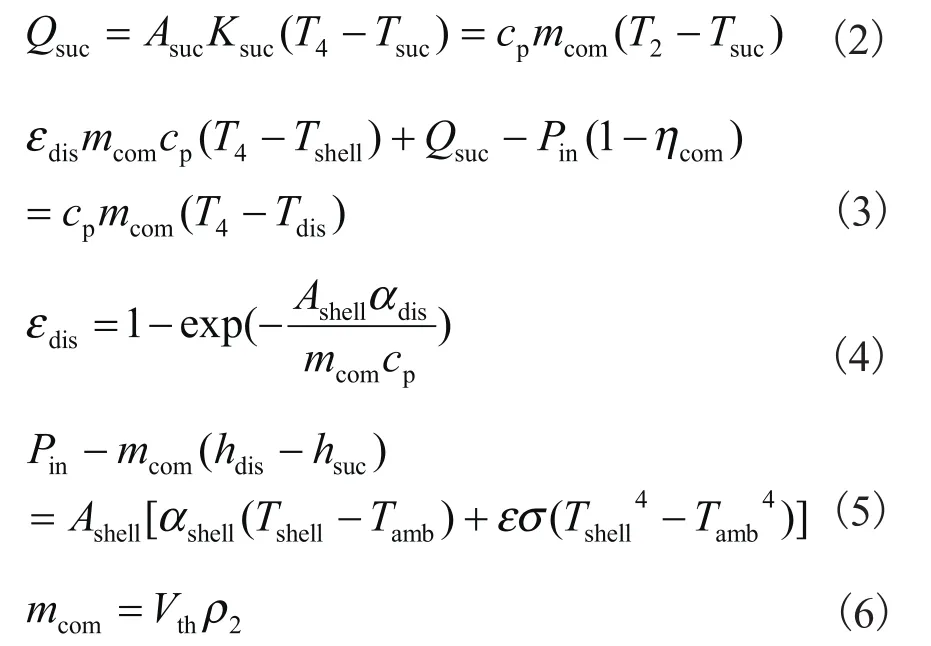
式中:Ksuc—吸气阶段总换热系数，其中吸气管内换热系数可视为强制对流，见文献[11]；管外换热系数可视为自然对流，见文献[12]；

αdis和αshell—为壳体与工质换热系数和壳体与环境换热系数，可视为自然对流，见文献[12]。

1.2 电子膨胀阀模型

膨胀阀模型的输入参数为膨胀阀入口工质的状态参数、膨胀阀背压，输出参数为工质流量。

工质流量可由以下公式求得:

式中:Cval—膨胀阀的流量系数，可由实验数据或厂家提供的标准测试数据进行标定；

Aval—膨胀阀的阀芯过流面积。

膨胀阀开度Aval对蒸发器出口过热度当前计算值ΔTsh,e,i与系统设定过热度ΔTsh的差值进行控制，使得系统平衡时计算所得过热度与设定过热度相等。对膨胀阀开度的调整采用PID控制算法中的比例环节(即去除含时间因素的积分和微分环节):

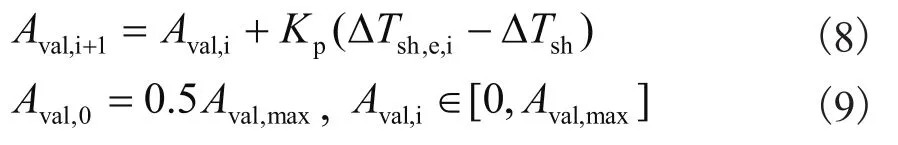
式中:Kp —比例常数；

Aval,max、Aval,0、Aval,i和Aval,i+1—阀最大开度、开度初值、当前迭代步和下一迭代步开度。

1.3 板式换热器模型

板式换热器中工作流体为逆流流动。模型输入参数为入口工质状态参数、工质流量、水流量和入口水温，输出参数为出口工质状态参数以及出口水温。

一维分布参数模型被建立，换热器沿工质流动方向被划分成若干控制容积，对于第每个控制容积建立能量方程:

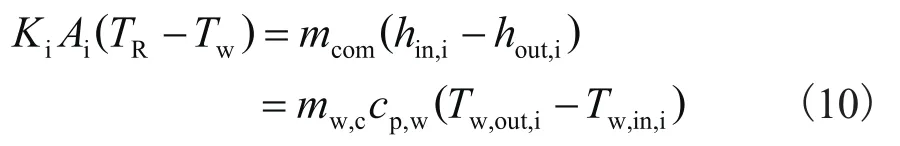
式中:Ki—控制容积总换热系数，其中冷凝或蒸发换热系数可采用Yan模型[13]，单相换热系数可采用Dittus and Boelter模型[14]；

换热器总压降Δp可用式(11)来计算:

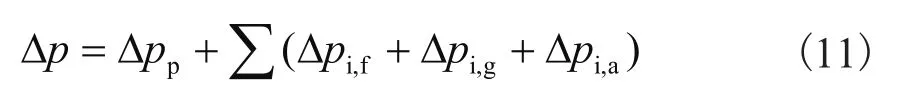
式中:Δpp—进出端口与分配器压降，可用式(12)计算；

Δpi,f、Δpi,g、Δpi,a—控制容积的摩擦压降、重力压降和加速压降。

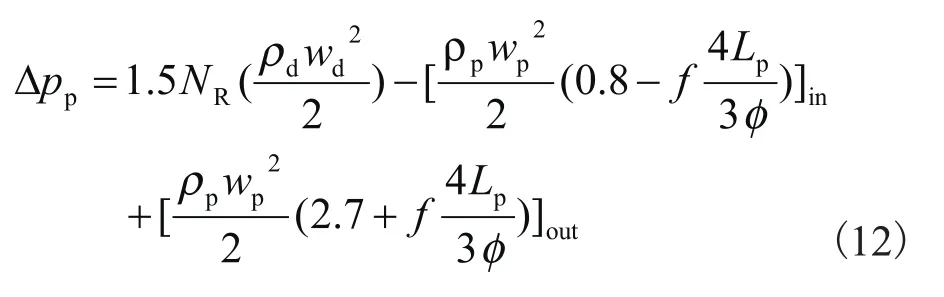
1.4 充注量模型

系统的工质绝大多数分布在两器以及冷凝器出口到节流装置入口的液管内。系统充注量ch可表示为换热器两相区工质质量和换热器单相区以及液管内工质质量之和:

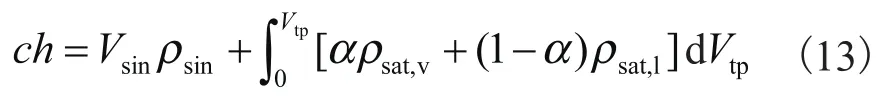
式中:Vsin—换热器单相区和液管内容积；

Vtp—换热器两相区工质侧内容积；

2 系统算法

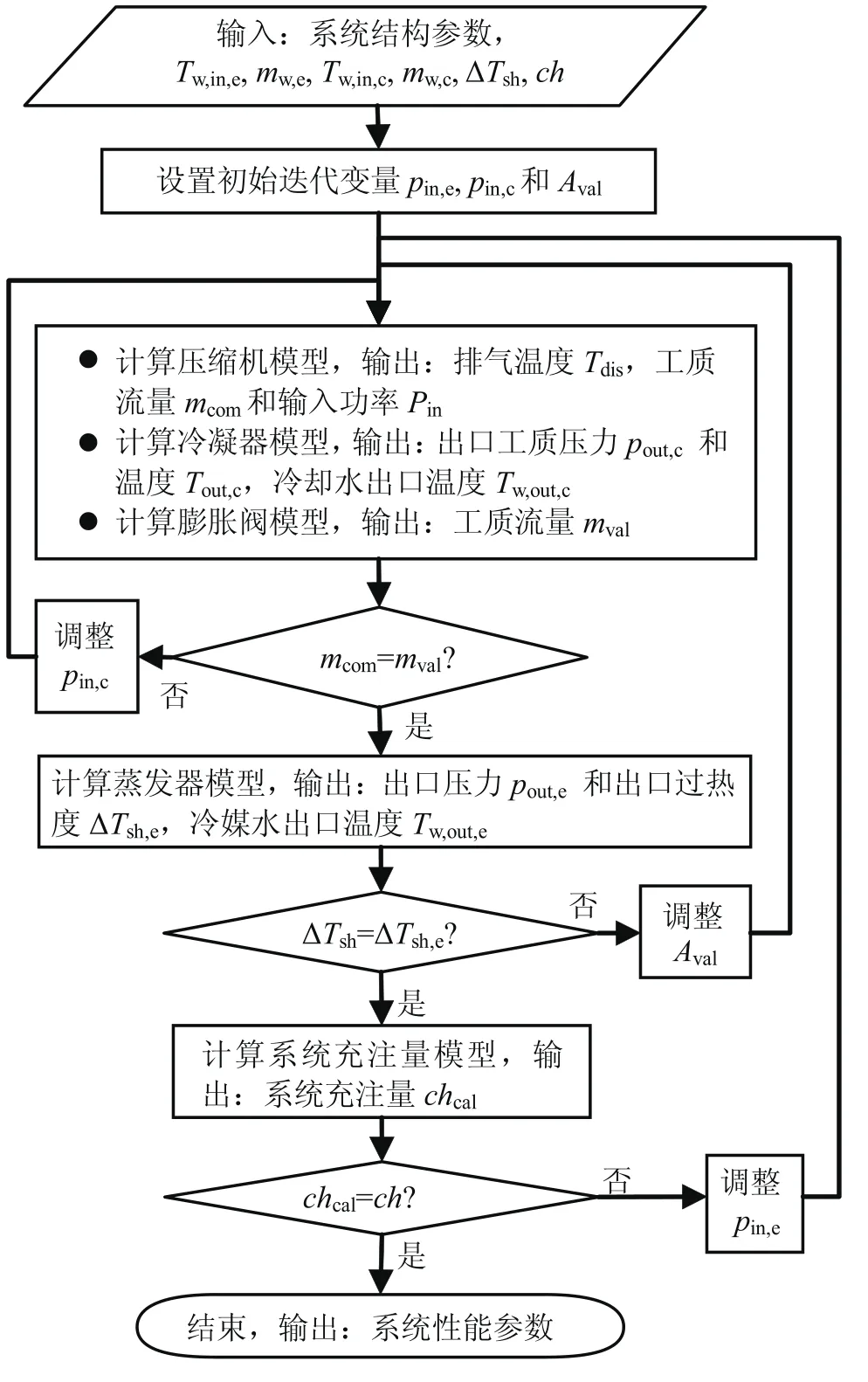
图2 系统算法流程图Fig.2 Flow chart of systematic algorithm

系统模型是通过系统算法将部件模型组合一起，模拟系统的性能参数。系统仿真模型的输入参数为系统结构参数，冷却水进口温度Tw,in,c、冷却水流量mw,c、冷媒水进口温度Tw,in,e、冷媒水流量mw,e、压缩机入口过热度设定值ΔTsh以及系统充注量ch。

结合连续迭代法和顺序模块法，将部件独立成模块。部件模块内采用小规模的连续迭代求解。系统层面，按顺序计算各个部件模块(即顺序模块法)，并设置系统平衡判据，用连续迭代法求解得到系统平衡。将部件模块化处理，提高了模型的可维护性，而部件内部和部件之间的小规模连续迭代保证了求解的稳定性和速度。图2为系统算法的流程图，具体说明如下:将热泵系统的工质回路从压缩机吸气口断开，设定系统初始迭代变量(蒸发器入口压力pin,e、冷凝器入口压力pin,c以及电子膨胀阀开度Aval)，然后计算从压缩机模块开始，并按照工质流动的方向对部件模块逐一计算，前一模块的输出参数作为下一模块的输入参数。另一方面，通过三层迭代计算调整pin,e、Aval和pin,c三个参数(即连续迭代法)，使系统最终达到能量和质量平衡。其中，pin,e和pin的调整采用两分法。

3 模型验证

利用涡旋式水源热泵性能测试台进行了水源热泵测试实验，用得到的实验数据对模型的预测精度进行了验证。测试台为单级蒸汽压缩涡旋式热泵循环，由三个回路构成，分别是工质回路，冷媒水回路和冷却水回路，其中水回路流量采用变频泵控制，控制原理为PID反馈控制:流量计测得实际流量，与设定流量进行比较，经变频器系统内置的PID调节器运算，输出频率控制信号调节输出频率，从而达到控制流量的目的，实际流量与设定流量的误差控制在±1%以内。温度测量采用K型热电偶，精度为0.3˚C；高压以及低压侧压力测量采用L520447型号压电式压力传感器，精度为0.05×105Pa；水侧流量测量采用体积流量计，精度为±0.8%。试验台在5个工况下进行测试，每个工况在基本稳定后以一定时间间隔进行采样，取采样点平均值作为该工况的最终实验值。

工质采用R134a。5组实验工况的实验参数如表1所示。模型预测的结果如图3所示。

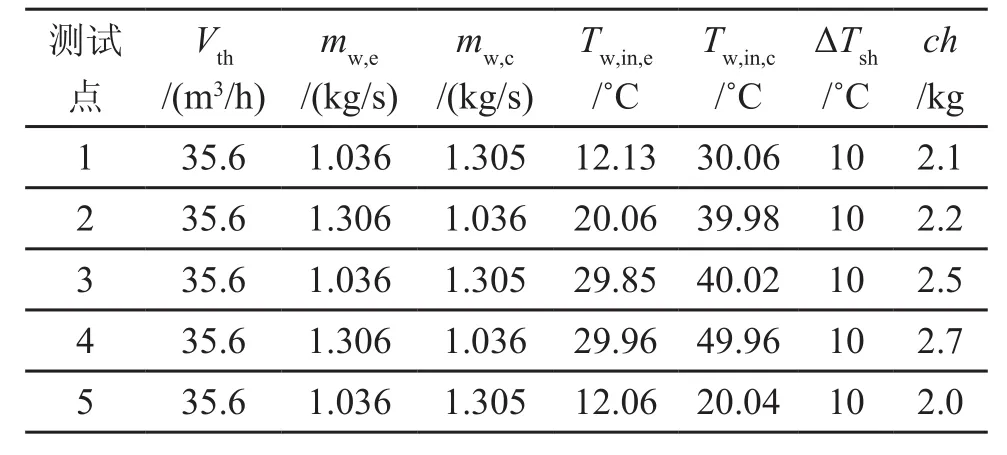
表1 热泵的实验参数(仿真主要输入参数)Tab.1 Experimental parameters of water source heat pump(main input parameters of simulation)

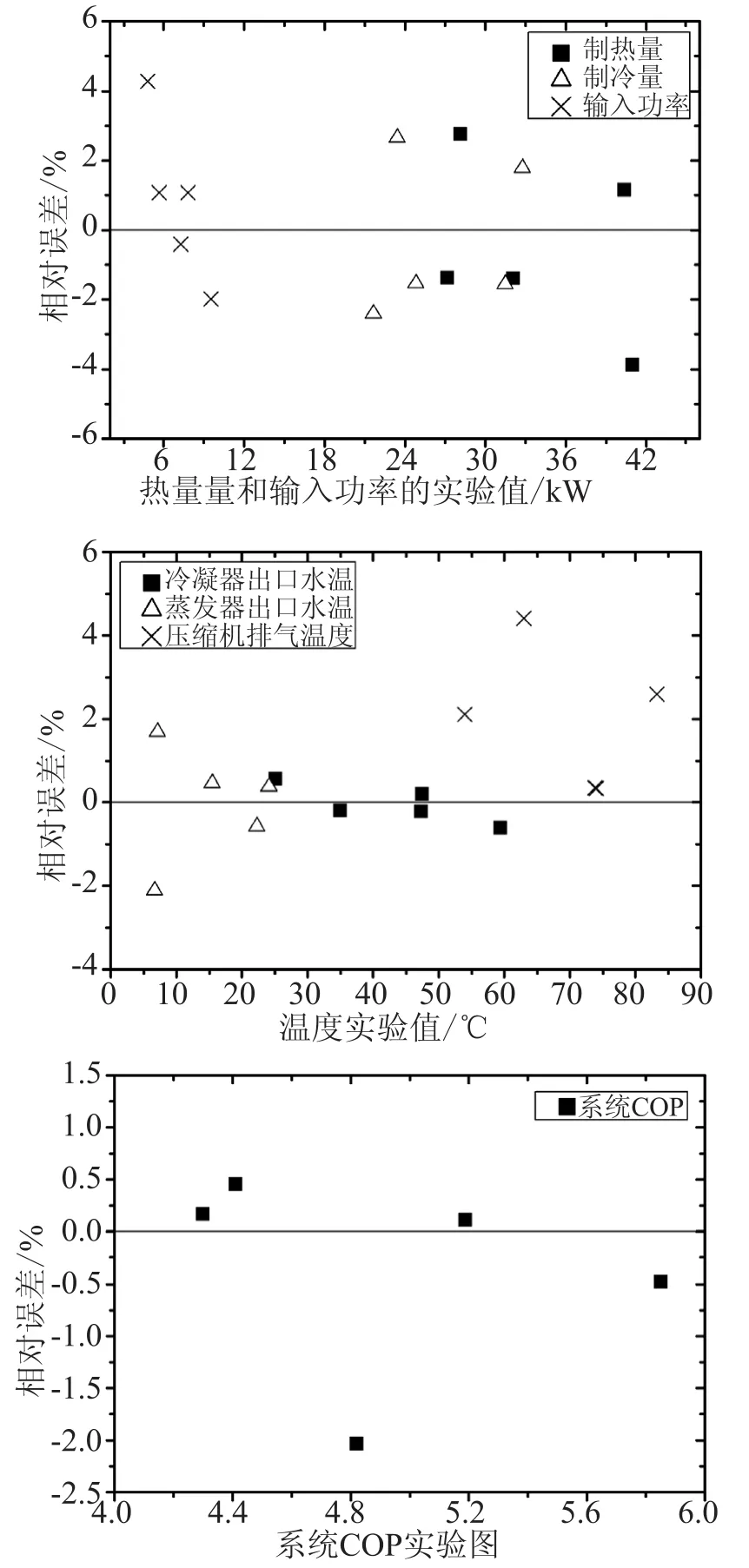
图3 模型预测值与实验结果对比Fig.3 Comparison between model prediction value and experimental data

4 系统分析

这里将利用已建立的系统仿真平台对涡旋式水源热泵的参数敏感性做一些分析，探讨冷两器水流量和入口水温等参数对系统性能的影响。

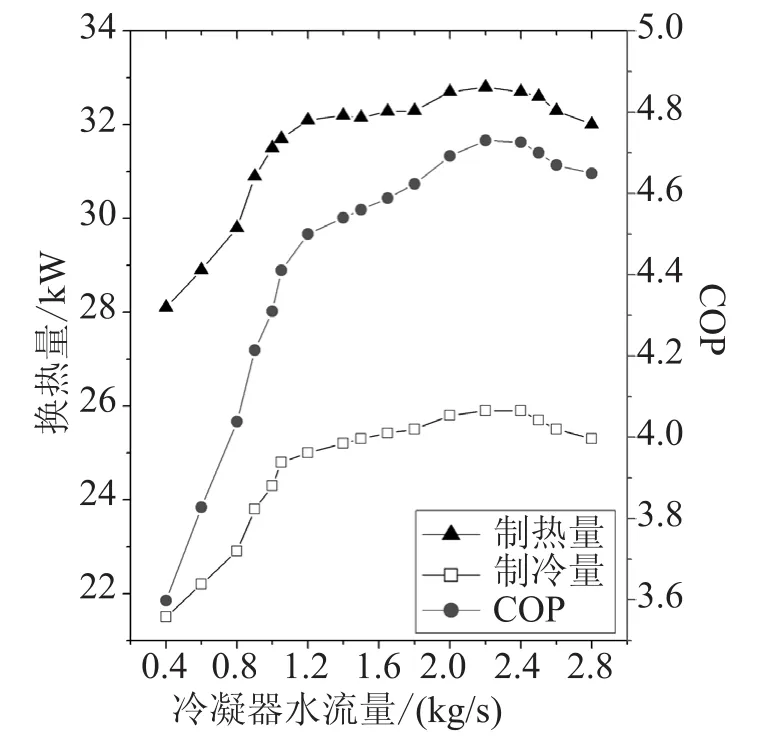
图4 (a)制热量、制冷量和COP 随冷凝器水流量的变化Fig.4(a) Variation of parameters with mass flow of cooling water

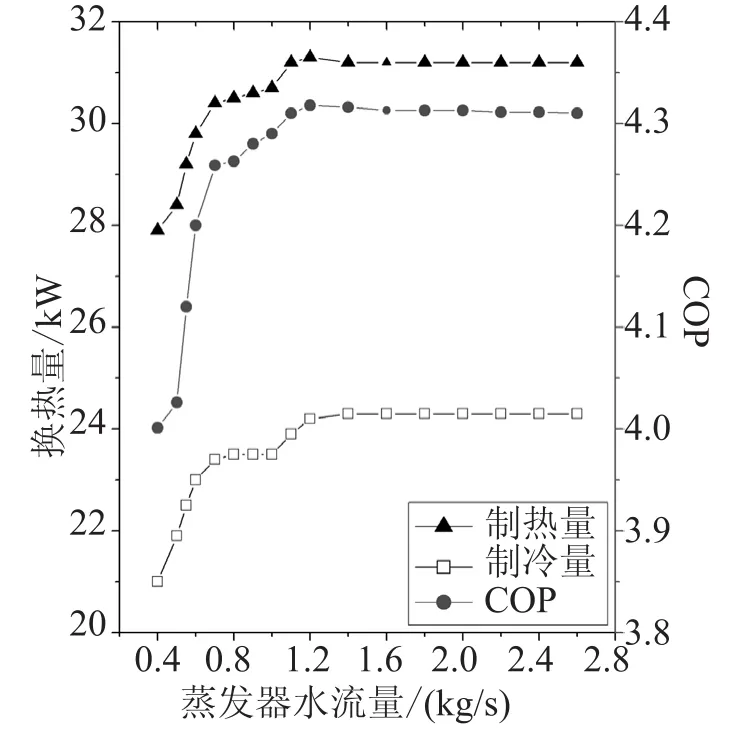
图4 (b)制热量、制冷量和COP 随蒸发器水流量的变化Fig.4(b) Variation of parameters with mass flow of chilled water

图4(a)反映了冷凝器水流量的变化对制热量、系统COP以及制冷量的影响。可以发现，虽然在小流量的情况下，各参量随水流量的增加而迅速增加，但达到一定值之后变化趋缓甚至下降。这是因为:小流量情况下，水流量增加可导致传热温差和换热系数增大，从而改善冷凝器换热，增加COP。同时蒸发器的进口焓变小，制冷量增加。但对于充注量一定的系统，当水流量继续增加，冷凝器出口过冷度增加，换热温差和平均传热系数变小，导致制热量和COP变化趋缓甚至下降。同时过冷段占的工质过多导致蒸发器中缺少工质，从而制冷量略有下降。

图4(b)反映了蒸发器水流量的变化对制热量、系统COP以及制冷量的影响。可以发现，虽然在小流量的情况下，各参量随水流量的增加而迅速增加，但达到一定值之后变化趋缓甚至下降。这是因为:小流量情况下，水流量增加可引起换热系数和冷热流体温差增加，从而制冷量增加，同时由于膨胀阀增大开度对过热度进行控制，引起工质流量变大和压缩机压差减小，从而制热量增加，功耗减小。但对于过热度受膨胀阀控制的系统，当水流量继续上升，阀开度的增大会导致蒸发压力上升，从而制冷量变化趋缓。而工质流量的进一步增大则抵消了前期压缩机压差变小对功耗的影响，并且导致冷凝器出口干度变大，换热恶化，从而制热量和COP变化趋缓甚至下降。

5 结论

建立了涡旋式水源热泵系统的稳态仿真模型，并设计了系统算法对该模型进行了求解。

压缩机模型方面，考虑了吸、排气换热以及能量流动对工质流量和排气温度的影响，同时只需少量结构参数。验证结果表明排气温度以及输入功率的预测误差在±4.2%以内。电子膨胀阀方面，增加膨胀阀开度对蒸发器过热度的控制算法避免了以往研究中将阀开度设为定值处理导致的开度输入值难以确定和精度不够的问题。系统算法方面，通过结合连续迭代法和顺序模块法，避免了前者处理大规模迭代问题时收敛性差以及后者在速度和健壮性方面的劣势，保证了系统模型求解的健壮性和易维护性。

开发的模型能够较好的预测涡旋式水源热泵稳态性能参数如换热量、压缩机输入功率、系统COP、冷却水出口温度和冷媒水出口温度等，预测精度范围在±4.4%以内。利用模型对热泵系统的分析表明，由于系统中充注量的分配和电子膨胀阀的控制作用，冷凝器和蒸发器水流量存在一个最优值，在该值下两器换热量和系统COP能达到最大。

[1] 丁国良, 张春路. 制冷空调装置仿真与优化[M]. 北京:科学出版社, 2001.

[2] 伏龙. 螺杆式制冷机组仿真的研究及应用[D]. 上海: 上海交通大学动力与能源工程学院, 2003.

[3] P Haberschill, S Borg, M Mondot, et al. Hermetic compressors models determination of parameters from a minimum number of tests [C], Purdue International Compressor Engineering Conference Proceedings, 1994:133-138.

[4] E Winandy, O C Saavedra, J Lebrun. Experimental analysis and simplified modeling of a hermetic scroll refrigeration compressor[J]. Applied Thermal Engineering,2002, 22: 107-120.

[5] Marie-Eve Duprez, Eric Dumont, Marc Frere. Modeling of reciprocating and scroll compressors[J]. International Journal of Refrigeration, 2007,30: 873-886.

[6] 陈文勇, 陈芝久, 等. 电子膨胀阀调节蒸发器过热度的控制算法[J]. 上海交通大学学报, 2001, 35(8):1228-1232. (Chen Wenyong, Chen Zhijiu, etal. Control algorithm for electrical expansion valve to adjust superheat of evaporator[J]. Journal of Shanghai Jiaotong University, 2001, 35(8): 1228-1232.)

[7] Fu Long, Ding Guoliang. Steady-state simulation of screw liquid chillers[J]. Applied Thermal Engineering,2002, 15: 1731-1748.

[8] Bourdouxhe J H, Grodent M, Lebrun J J, et al. A toolkit for primary HVAC System energy calculation, Part 2:Reciprocating chiller models[J]. ASHRAE Transactions.1994, 100(2): 774-786.

[9] Jolly F G, Tso C P, Wong Y W, et al. Simulation and measurement on the full-load performance of a refrigeration system in a shipping container[J]. International Journal of Refrigeration, 2000, 23: 112-126.

[10] U. Van Houte, E. Van den Bulck. Modelling chiller performance using simulations equation-solving procedures[J]. International Journal of Refrigeration,1994, 17 (3): 191-198

[11] 王启川. 热交换器设计[M]. 台北:五南出版社，2007.

[12] M. Fukuta, T. Yanagisawa, T. Shimizu, Compression characteristics of refrigerant–oil mixture in refrigerant compressors[J]. Trans. Jpn. Soc. Mech. Eng, 1995, 61(582): 542–548.

[13] Y Y Yan, H C Lio, T F Lin. Condensation heat transfer and pressure drop of refrigerant R134a in a plate heat exchanger[J]. International Journal of Heat and Mass Transfer, 1999, 42 (6): 993–1006.

[14] FW Dittus, LMK Boelter. Heat transfer in automobile radiators of the tubular type[J]. University of California Publications in Engineering, 1930, 11: 443-461.