舰载旋转机械基础冲击响应建模和数值计算＊

贺少华，吴新跃

（海军工程大学船舶与动力学院机械工程系，湖北 武汉430033）

对于舰载设备在水下非接触爆炸冲击环境中的响应研究，目前，海军部门使用的规范冲击动力学分析方法只能针对设备静态时的情况，对于动态运行时设备的冲击响应则简单地规定为静态响应与工作载荷的绝对值相加，忽略了冲击激励与设备动态运行工作载荷的耦合，对于动态即设备运行条件下的冲击响应还没有标准的建模计算方法。对于旋转机械来说，相对静态非工作条件，动态工作条件下的冲击响应无疑更有研究价值。本文的主要目的就是要建立一套标准的运行条件下旋转机械冲击响应建模和计算理论方法，并将其运用于工程实际。

对舰载旋转机械即转子－轴承系统的冲击响应研究，主要方法为：首先对转子－轴承系统建模，用基础运动（位移、速度和加速度）来模拟基础冲击，建立系统动力学方程；然后通过数值计算求解方程得到响应。通过响应分析检验以下几个方面的内容：（1）润滑油膜在任何时候必须保持一个最小的油膜厚度以避免转子和轴承发生碰摩；（2）轴承基础能够承受冲击轴承反力；（3）转子冲击应力在安全范围内。

以往的类似研究［1－4］主要采用了刚体模型和梁模型两种转子建模方法：刚体模型在对润滑油膜厚度进行预测和轴承反力的计算上是足够合适的，此时转子一般仅由2个轴承支撑。这种建模方法牺牲了精确性，因为它忽略了转子的柔性，但还是可以得到一些有意义的分析结果，而且避免了复杂的数学建模和计算问题。当转子由2个以上轴承支撑，或者需要考察转子本身受冲击时的应力和变形时，梁模型就成为了首选。

本文中，将采用Galerkin有限单元模型来对转子进行建模，使计算实际复杂舰载旋转机械设备的冲击响应成为可能，而不是仅局限于简单抽象的转子－轴承系统。根据水下非接触爆炸冲击在舰船设备基础处形成的冲击环境的特点，冲击激励只考虑平动形式，不考虑转动形式。

1 基础冲击动力学方程

考虑一个弹性圆形截面转子（轴）单元绕它的轴旋转和在空间做任意运动。它的任意瞬时运动状态可以通过欧拉角来描述。如图1所示，XYZ为全局惯性坐标系，原点位于初始时刻单元的质心G；xyz为随动坐标系，xyz随单元进行绕x轴的转动，角度设为θ；绕y轴的转动，角度设为ψ，但它不随单元绕其自身z轴转动。此外，对于单元自身来说，还有绕z轴的转动，角度设为φ。根据牛顿运动和动量矩定律，单元的力学方程有

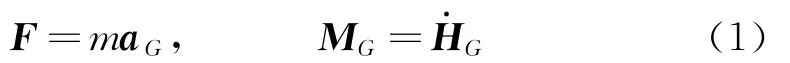
式中：F为单元所受合力，aG为单元质心的绝对加速度，MG为外力对质心的主矩，HG为单元对质心的角动量距。的一般表达式为

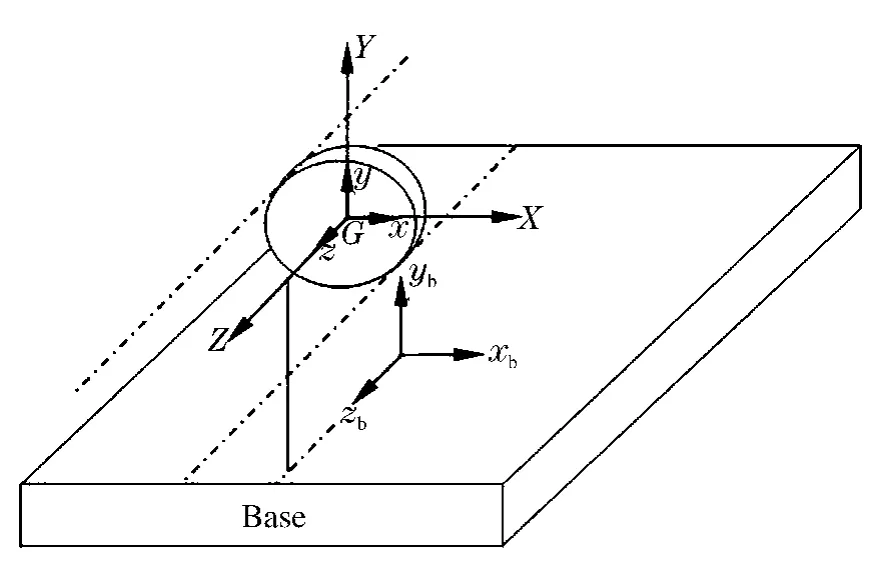
图1 转子单元、基础及其坐标系Fig.1Rotor element，base and their coordinate system

式中：ρ为材料密度，ds为单元长度，IP为轴段单元截面极惯性矩，IT为截面赤道惯性矩，对于圆形截面，IP＝2IT。

转子由轴承支撑，轴承基础被认为是刚性的，附连参考坐标系为xbybzb。坐标系的方向和原点位置如图1所示。轴承润滑油膜提供刚度和阻尼给轴承与转子的相对运动。在冲击响应分析中，轴承基础施加已知的加速度冲击激励，分析的目的就是要预测转子的瞬态响应。

冲击激励将使基础从平衡位置发生偏离，偏离以平移运动形式存在。由于基础的运动，将导致转子从平衡位置也发生偏离，以平移和转动2种形式存在。

单元的质心相对xbybzb坐标系的微小平动位移设为ux、uy、uz，类似地，单元的质心相对xbybzb坐标系的微小转动位移设为θx、θy、θz。因为θx、θy、θz一般为小量，所以他们的转动顺序可以不予考虑，因此有下面的关系式

另外，前面已经假定单元的自转（绕z轴）角速度是恒定的，即＝ω（为定值）＝0。

将式（3）代入式（2），能够得到以下表达式

在上述表达式中，包含IPω项即为由于转子旋转带来的陀螺惯量项。单元质心G的绝对加速度为

即为基础加速度冲击运动激励。从式（4）、（5）可以看出，在单元的动力学关系式中，旋转惯性力、陀螺效应和基础运动激励都被考虑进来。

单元的自由体受力分析（在ybzb和xbzb平面的情况）如图2所示，根据Timoshenko梁理论，横向剪切力的表达式为

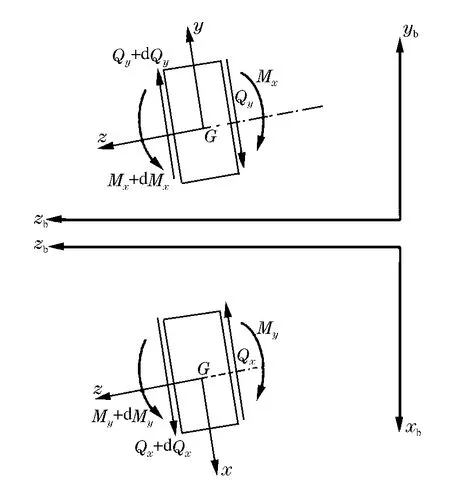
图2 单元受力分析Fig.2Load analysis for the rotor element

式中：k为Timoshenko系数，H为材料刚性模量，A为单元横截面积。弯矩表达式为

综上所述，考虑轴承油膜支撑力得到单元总的受力和力矩表达式为

轴承油膜力fx、fy在这里可以采用8系数油膜力模型，即

考虑工作载荷轴向力Tp和扭矩Mp的对应于方程（8）的单元受力和力矩表达式为

综合以上各式，方程组（1）可以具体化为

以上4式加上式（6）和式（7）中的4式总共8个方程，未知数也为8个：2个剪切力Qx、Qy，2个弯矩Mx、My，2个平动位移ux、uy，2个转动位移θx、θy（不考虑z向的情况）。

2 方程的求解、算法的程序编制和理论的准确性验证

由以上推导结果可知，系统的动力学微分方程为偏微分方程，包含空间变量s和时间变量t，可以尝试在空间域采用有限单元法和在时间域采用直接积分法。在本文中，利用Galerkin方法和有限单元法将系统偏微分方程转化为常微分方程，然后采用Newmark直接积分方法迭代求解响应时间历程，Newmark直接积分方法无条件稳定，在瞬态响应计算中最常用［5］。最终得到系统总的运动微分方程形式为

式中：qe为节点位移向量，包括2个平动位移ux、uy和2个转动位移θx、θy；Me为系统质量矩阵；Ce为阻尼矩阵，由2部分组成，一部分为陀螺矩阵，另一部分为轴承阻尼带来的阻尼矩阵；Ke由4部分组成，第1部分为轴单元本身刚度项，第2部分为工作轴向力Tp带来的刚度项，第3部分为工作扭矩Mp带来的刚度项，第4部分为轴承刚度项；Qe为节点力和力矩载荷向量。

在ANSYS－APDL软件平台上，首先建立单元模型，然后根据式（12）组装各系数矩阵，最后采用Newmark法进行迭代程式求解。算法程序的部分内容可以直接利用软件本身提供的功能，如（冲击）瞬态响应计算的Newmark法程式、转子（轴）单元的插值函数等。计算完成后，利用软件的后处理功能描绘和显示计算结果即响应的时间历程。

以一个简单转子系统的自由振动来验证本文方法的可靠性，即令式（12）的右边等于零，该简单转子系统的相应参数参考文献［6］。由于考虑了陀螺力矩，所以转子有4个进动角速度，其中2个值大于零，为正进动的频率f＋，另2个值小于零，为反进动的频率f－。将本文方法计算结果与精确解对比如表1所示。对比计算结果可以发现，本文方法计算结果与精确解吻合较好，证明了本文建模理论的正确性。

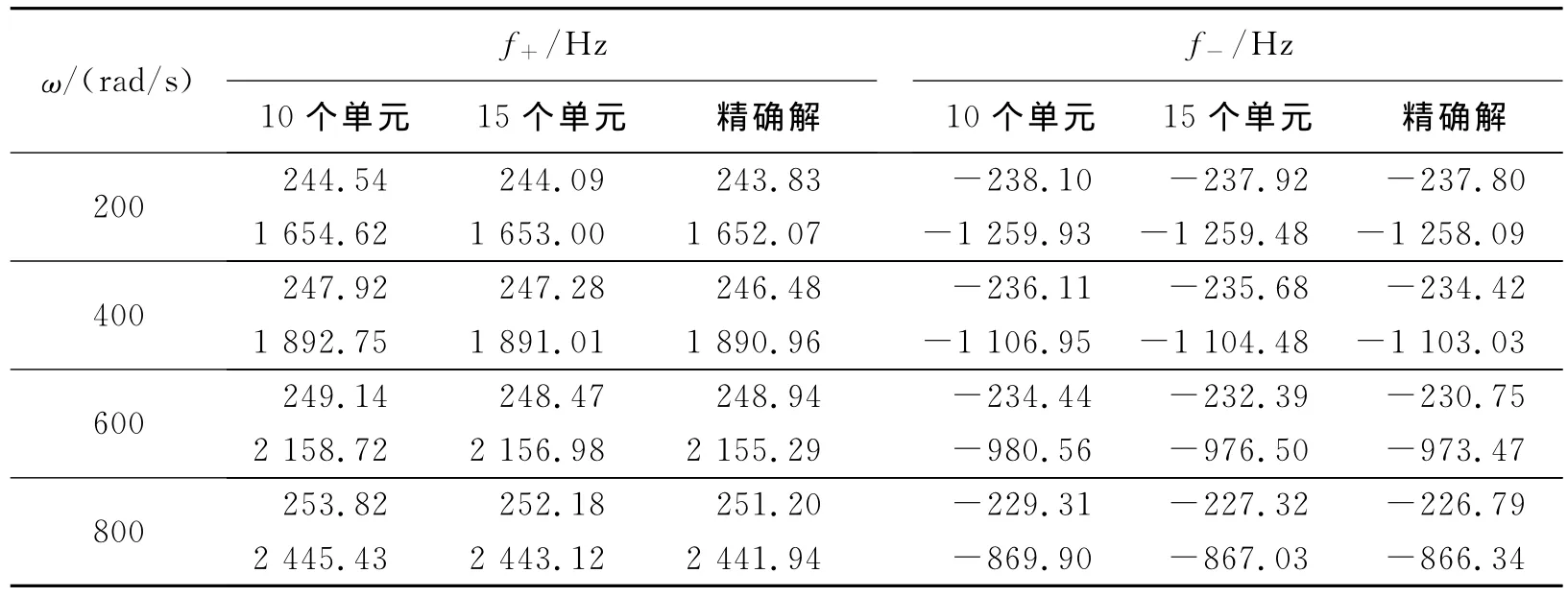
表1 自由振动固有频率对比Table 1Comparison of free－vibration frequencies

3 工程应用

一实际旋转机械转子系统模型如图3所示，具体的系统参数为：E＝200GN／m2，ρ＝7.8t／m3，刚性圆盘m＝500kg，IP＝250kg·m2，IT＝126.7kg·m2。轴承参数为：（kxx）1＝0.589GN／m，（kxy）1＝（kyx）1＝ －1.290GN／m，（kyy）1＝1.870GN／m，（kxx）2＝0.676GN／m，（kxy）2＝ （kyx）2＝－1.490GN／m，（kyy）2＝2.270GN／m。冲击加速度激励形式如图4所示，该冲击加速度形式取自联邦德国海军规范BV0430［7］，其正反双波的形式最能模拟水下非接触爆炸在舰载设备基础处形成的冲击环境。冲击加速度激励持续时间为100ms，计算时间为500ms。

图3 计算实例转子－轴承系统模型Fig.3Model of a rotor－bearing system

图4 基础冲击加速度激励形式Fig.4Base shock excitation in acceleration form

3.1 转速（陀螺效应）对响应的影响

考察陀螺效应即转速对响应的影响。得到的计算结果为：当转速ω为0、500、1 000、1 500、2 000、3 000rad／s时，单元的最大瞬时应力Qy分别为390、352、431、400、427、459MPa。从计算结果可以发现，陀螺效应即转速对冲击响应的影响是明显的，不同转速下应力响应最大差别达30%。从本文计算结果来看，随转速的升高响应似乎也随之升高，但这不具有普遍意义，因为本文作者在另一工程应用中计算得出了具有相反特征的结果［8］，所以，陀螺效应对冲击响应的影响应该是具体问题具体分析，不同的冲击激励和不同的对象可能会有不同的影响规律。

3.2 工作载荷对响应的影响

考察工作载荷对系统响应的影响规律，并求解冲击激励和工作载荷共同作用下的系统响应规律。对于旋转机械系统如推进轴系来说，在运转状态除要承受陀螺力和旋转惯性力外，还要承受工作负荷带来的扭矩、轴向力等载荷，上文中已经建立了考虑这些载荷的冲击动力学理论模型。在本工程实例中，假定系统工作载荷为轴向力100MN。经计算，该工作载荷产生的稳态应力值Qy＝800MPa。表2所示为工作载荷对系统固有频率的影响，工作稳态应力使得系统固有频率增大，等效于系统刚度变大。

表2 固有频率对比Table 2Comparison of natural frequencies Hz

图5（a）、（b）分别为不考虑和考虑工作载荷时某相同位置的应力响应时间历程（转速ω＝500rad／s）。不考虑工作载荷即式（11）中的Tp、Mp均等于零，此时系统响应的主要决定因素为陀螺效应即IPω项；考虑工作载荷时，陀螺效应IPω和工作载荷Tp、Mp共同对响应结果产生影响。可以发现，考虑工作载荷时的冲击响应≠工作载荷下稳态响应＋不考虑工作载荷时冲击响应，就关心的最大瞬时应力而言，前者要明显大于后者，即图5中的：2 050＞800＋352。而从20世纪90年代初沿用至今的GJB1060.1－91［9］中的冲击规范部分却规定“动力学分析得到的冲击应力与分析系统的运行特性如旋转力、蒸汽压力等产生的连续工作应力的应力综合为两者的绝对值相加”，很显然，该项标准受当时计算条件的限制和出于简单的考虑，从本文的研究结论可以看出，已经不合时宜，需要进行修正。

图5 相同位置应力响应时间历程Fig.5Time－varying stress response at the same position

4 结 论

建立了一套旋转机械转子－轴承系统基础冲击响应的理论建模方法，基于的理论主要有牛顿运动定理、动量矩定理、Timoshenko梁理论和有限元理论，方程全面综合考虑了各种物理因素：旋转惯性力、剪切力、陀螺效应、轴向力、轴向扭矩以及轴承的油膜力，克服了以往类似研究考虑条件单一的缺点，同时，本文研究也使得运行状态下旋转机械的冲击响应计算成为了可能，而目前海军部门舰载机械设备冲击响应计算还只能针对静态的情况。通过对一工程实例的解算，得到了一些重要的结论，概括起来主要有：陀螺效应对响应影响明显，陀螺效应对冲击响应的影响应该是具体问题具体分析，不同的冲击激励和不同的对象可能会有不同的影响规律；考虑工作载荷时的冲击总响应不是工作载荷稳态响应与不考虑工作载荷时的冲击响应的简单相加，两者差别较大，需要对GJB1060.1－91相关条文进行修正。

［1］Hori Y，Kato T.Earthquake－induced instability of a rotor supported by oil film bearings［J］.Journal of Vibration and Acoustics，1990，112（2）：160－165.

［2］Singh M P，Chang T S，Suarez L E.A responses spectrum method for seismic design evaluation of rotating machines［J］.Journal of Vibration and Acoustics，1992，114（2）：454－460.

［3］Gaganis B J，Zisimopoulos A K，Nikolakopoulos P G，et al.Modal analysis of rotor on piecewise linear journal bearing under seismic excitation［J］.Journal of Vibration and Acoustics，1999，121（2）：190－196.

［4］Victor V K，Andrei V P，Peter S V.An advanced seismic analysis of an NPP powerful turbogenerator on an isolation pedestal［J］.Nuclear Engineering and Design，2007，237（12／13）：1315－1324.

［5］An S L，Byung O K.A finite element transient response analysis method of a rotor－bearing system to base shock excitations using the state－space Newmark scheme and comparisons with experiments［J］.Journal of Sound and Vibration，2006，297（3／4／5）：595－615.

［6］钟一谔.转子动力学［M］.北京：清华大学出版社，1987.

［7］中国舰船研究院科技发展部.联邦德国国防军舰艇建造规范译文集－BV0430冲击安全性［S］.1998.

［8］贺少华，吴新跃.运转条件下推进轴系冲击响应计算［J］.中国造船，2011，52（4）：10－15.

HE Shao－hua，WU Xin－yue.Shock response analysis for propulsion shaft system in running state［J］.Shipbuilding of China，2011，52（4）：10－15.

［9］GJB1060.1－91.舰船环境条件要求机械环境［S］.