冲击载荷下猪后腿肌肉的横向同性本构模型＊

王宝珍，胡时胜

（中国科学技术大学中国科学院材料力学行为和设计重点实验室，安徽 合肥 230026）

在汽车安全、军事工程和医疗诊断中，都需要对人体受冲击状态进行分析，研究人体组织的冲击力学性能，并发展能描述其动态性能的本构关系，以得到相关的参数，对于安全设计等方面有着重要的意义。肌肉是人体组织中一个重要的组成部分，按性质的不同通常分为3类：骨骼肌、平滑肌和心肌。骨骼肌在人体中占有很大的比重，躯体的各种运动和呼吸均离不开骨骼肌。骨骼肌由许多平行排列的肌纤维及纤维间的结缔组织组成，其力学性能由肌纤维和结缔组织共同决定。与其他工程材料有很大不同的是，它可以产生2种不同形式的力，即主动力和被动力。

研究骨骼肌在外部冲击载荷作用下的被动承载能力，对人体安全设计有重要意义。但由于肌肉组织具有一定的活性，试样获取困难，且极其柔软，给实验特别是动态实验带来了很大的困难，因而相关研究很少。B.Song等［1］、C.Van Sligtenhorst等［2］曾利用SHPB装置获得了肌肉的动态压缩应力应变曲线，但其动态拉伸性能还无相关报道。为弥补这一空白，王宝珍等［3－4］利用改进的SHPB装置和套筒式SHTB装置对猪后腿肌肉的动态压缩和拉伸性能进行了研究，获得了不同应变率下的应力应变曲线。然而，描述肌肉材料动态力学性能的本构模型还需要进一步讨论。

关于骨骼肌的本构模型，以往的研究往往集中于描述肌纤维的主动收缩性能，如著名的Hill模型。而为了描述骨骼肌的被动力学性能，通常结合其特殊的纤维组织结构，将骨骼肌看作横向同性体。M.Van Loocke等［5］曾借用横向同性弹性理论，并引入应变相关杨氏模量，从而描述骨骼肌静态压缩下的非线性横向同性性能。J.D.Humphrey等［6］则从另一种思路出发，将肌肉看作纤维增强复合材料，在参考构形中，引入一个纤维方向的单位矢量，由该方向矢量与右Cauchy－Green变形张量可表述出5个应变不变量，他们将应变能密度函数用这5个应变不变量来表示，从而发展了描述心肌被动力学性能的横向同性超弹性本构模型，后被许多学者用于研究骨骼肌［7－8］的横向同性超弹性。然而，由于一直以来缺乏肌肉动态性能研究的实验结果，因而未能得到一个描述肌肉动态性能的率相关本构模型。

本文中，将结合已有的猪后腿肌肉动态压缩和拉伸实验结果，发展一个既能描述肌肉动态压缩性能又能描述其动态拉伸性能的率相关本构模型。

1 纤维增强材料应变能函数表示方法

肌肉、韧带等生物软组织通常可看作是柔性基质中分布了一簇簇连续纤维的复合结构。对于纤维增强复合材料，A.T.M.Spencer［9］提出了由5个应变不变量表示横向同性超弹性应变能函数的方法，该方法被一些研究者应用于生物软组织材料的本构模型研究中，并发现行之有效［10］。

式中：N0＝n0⊗n0为对称的二阶张量，单位方向矢量n0（X）表示各向异性材料的对称轴方向。其中I1、I2和I3表示材料的各向同性，在不可压假定下，I3＝1。不变量I4和I5用来表示材料的各向异性。则不可压纤维增强材料的应变能函数可表示为

通常可将式（2）进行解耦，以便与材料的结构特征相联系，如

式中：W1代表各向同性基体组织的力学性能，W2用来代表具有纤维集合的增强作用，W3表示纤维和基体之间的相互作用。

2 粘弹性性能

粘弹性材料最大的特点就是力学性能受之前变形的影响，应力依赖应变和应变率历史，对于不可压各向同性材料的粘弹性本构模型通常用下式来表示

式中：σv、pv分别为表征粘弹性性能的Cauchy应力和静水压力；Ω是张量泛函，反映应变历史对应力的影响，前人已经提出了多种形式的泛函的近似表达式，如BKZ模型、ZWT模型，这些模型通常采用积分形式来表示。

对于软组织材料，Z.A.Taylor等［11］曾采用类似的积分形式来表示横向同性粘弹性性能，即

3 肌肉的本构模型

按照前文的本构理论，将描述准静态下的本构模型与描述粘弹性性能的本构模型进行简单的相加，以表示肌肉的动态本构模型，那么总的Cauchy应力可分为2部分，一部分表征材料的准静态超弹性，一部分表征材料的粘弹性，即

3.1 肌肉准静态本构模型

取n0＝ （1 ，0 ，0） ，对于纤维向加载，假定纤维向伸长比为λ，则3个主伸长比为λ1＝λ，λ2＝λ3＝λ－1／2。 变形梯度F和右Cauchy－Green变形张量C可表示为

5个基本不变量可分别表示为

选用Yeoh模型［12］来描述基体的各向同性性能，即

假定肌纤维不能承受压缩载荷而仅能承受拉伸载荷，选用这样一个描述纤维伸长的应变能函数

式中：符号 〈x〉表示当x≤0时，〈x〉＝0，当x＞0时，〈x〉＝x。

对于纤维与基体的相互作用部分，参考J.C.Criscione等［13］提出的2个表示纤维向剪切和横向剪切性能的新变形不变量，并将其改写为

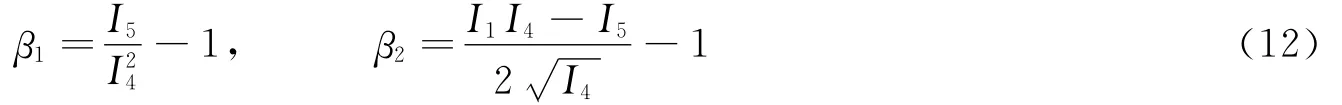
纤维与基体相互作用的那部分应变能函数表示为

将式（9）代入式（12），有

因此

则表征准静态超弹性性能的Cauchy应力分量可以表示为

图1 准静态肌肉纤维方向压缩和拉伸的应力应变曲线Fig.1Compressive and tensile stress－strain curves of muscle under quasi－static loading along the fiber direction

采用式（18）对纤维向单轴压缩和单轴拉伸曲线进行拟合，如图1所示。可得到参数C10＝821Pa，C20＝1.81kPa，C30＝－72.4Pa，a＝7.09kPa，b＝13.94。发现实验曲线和拟合曲线有很好的一致性。

3.2 动态本构模型

对纤维向动态压缩，仍假定肌纤维不承压，式（6）表示为

这里取

由实验得到的应力应变曲线，发现3 200s－1下的应力应变曲线与另2种应变率（1 100、2 000s－1）下的应力应变曲线间距较大，即在高应变率区，应变率增加时应变率敏感性增加，为描述这一现象，令

式中：为伸长速率，压缩为负，拉伸为正；A1、A2和均为材料参数。由式（19）～（21）可得到

同样，由σ22＝σ33＝0，可以得到

则动态单轴压缩时沿纤维方向的工程应力σ（＝σ11／λ）为

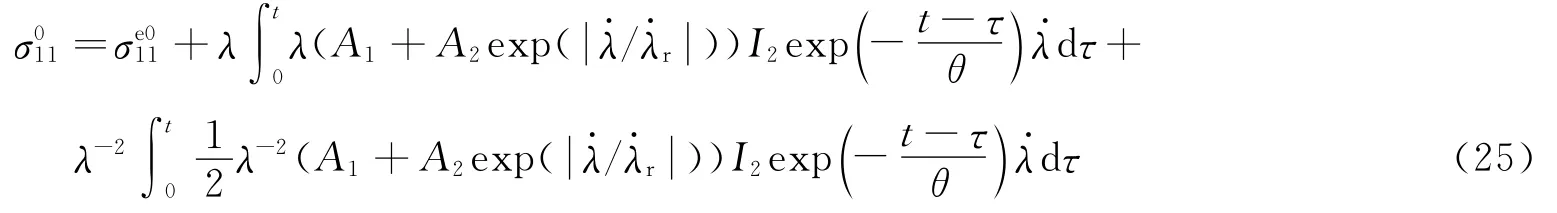
图2 高应变率下肌肉沿纤维方向压缩的应力应变曲线Fig.2Compressive stress－strain curves at high strain rates along the fiber direction

式中：由式（18）给出，采用上式对高应变率下纤维方向的动态压缩工程应力－伸长比曲线进行拟合，如图2，参数A1＝12.1kPa，A2＝15.4kPa＝1 237s－1，θ＝67.11μs。结果发现，拟合曲线与实验结果一致性较好。

为了描述纤维向动态拉伸的情况，需对式（25）进行修改，即在等号右侧增加2项：一项考虑肌纤维在拉伸时对粘弹性性能的贡献，另一项考虑动态拉伸应力应变曲线与动态压缩曲线形状的不同。动态拉伸曲线的初始阶段不存在低应力幅值区，而是有一类似屈服点的转折点，且动态实验结果在小应变时也并不可靠，因此拟合曲线时并非从零点开始，而是仅考虑该点以后的情况。最终得到动态单轴拉伸沿纤维方向的工程应力－伸长比本构关系为

式中：f（I4）＝A3〈I4－1〉／2，那么

图3 高应变率下肌肉沿纤维方向拉伸的应力应变曲线Fig.3Tensile stress－strain curves at high strain rates along the fiber direction

采用上式对高应变率下纤维方向的动态应力应变曲线进行拟合，如图3所示，参数A3＝300kPa，A4＝3kPa，A5＝3.09，发现理论模型与实验结果有很好的一致性。

4 结 论

肌肉软组织可看作是一种纤维增强复合材料。应用相关本构理论，提出了一个既能描述动态压缩力学性能又能描述动态拉伸力学性能的横向同性率相关本构模型，该模型由描述准静态响应的超弹性模型和描述高应变率响应的粘弹性模型组成，理论曲线与实验得到的应力应变曲线有很好的一致性。说明提出的模型能够很好地描述肌肉的力学性能，可为人体安全防护设计提供理论依据。

［1］Song B，Chen W，Ge Y，et al.Dynamic and quasi－static compressive response of porcine muscle［J］.Journal of Biomechanics，2007，40（13）：2999－3005.

［2］Sligtenhorst V C，Cronin D S，Brodland G W.High strain rate compressive properties of bovine muscle tissue determined using a split Hopkinson bar apparatus［J］.Journal of Biomechanics，2006，39（10）：1852－1858.

［3］王宝珍，胡时胜.猪后腿肌肉的冲击压缩特性实验［J］.爆炸与冲击，2010，30（1）：33－38.

WANG Bao－zhen，HU Shi－sheng.Dynamic compression experiments of porcine ham muscle［J］.Explosion and Shock Waves，2010，30（1）：33－38.

［4］王宝珍，郑宇轩，胡时胜.猪后腿肌肉的动态拉伸性能研究［J］.爆炸与冲击，2010，30（5）：449－455.

WANG Bao－zhen，ZHENG Yu－xuan，HU Shi－sheng.Dynamic tensile properties of porcine ham muscle［J］.Explosion and Shock Waves，2010，30（5）：449－455.

［5］Van Loocke M，Lyons C G，Simms C K.Viscoelastic properties of passive skeletal muscle in compression：Stressrelaxation behaviour and constitutive modelling［J］.Journal of Biomechanics，2008，41（7）：1555－1566.

［6］Humphrey J D，Strumpf R K，Yin F C P.Determination of a constitutive relation for passive myocardium［J］.Journal of Biomechanical Engineering，1990，112：333－346.

［7］Gielen A W，Oomens C W，Bovendeerd P H，et al.A finite element approach for skeletal muscle using a distributed moment model of contraction［J］.Computer Methods in Biomechanics ＆Biomedical Engineering，2000，3（3）：231－244.

［8］Martins J A C，Pires E B，Salvado R，et al.A numerical model of passive and active behavior of skeletal muscles［J］.Computer Methods in Applied Mechanics and Engineering，1998，151（3）：419－433.

［9］Spencer A J M.Continuum theory of the mechanics of fibre－reinforced composites［M］.New York：Springer－Verlag，1984：1－32.

［10］Limbert G，Middleton J.A constitutive model of the posterior cruciate ligament［J］.Medical Engineering ＆Phys－ics，2006，28（2）：99－113.

［11］Taylor Z A，Comas O，Cheng M，et al.On modelling of anisotropic viscoelasticity for soft tissue simulation：Numerical solution and GPU execution［J］.Medical Image Analysis，2009，13（2）：234－244.

［12］Yeoh O H.Characterization of elastic properties of carbon－black－filled rubber vulcanizates［J］.Rubber Chemistry and Technolog，1990，63（5）：792－805.

［13］Criscione J C，Douglas A S，Hunter W C.Physically based strain invariant set for materials exhibiting transversely isotropic behavior［J］.Journal of the Mechanics and Physics of Solids，2001，49（4）：871－897.