内置式永磁同步电动机转子结构的优化设计

刘 坚，黄守道，浦清云，程泽高

(湖南大学，湖南长沙410082)

0 引 言

随着永磁材料性能的不断提高，永磁电机越来越广泛地应用于高性能的控制系统中。相对于传统的电励磁电机，永磁电机具有体积小、重量轻、能量密度高、效率和功率因数高等优点。然而永磁电机中，齿槽转矩产生的振动和噪声及转动惯量过大是影响其控制精度的主要原因，因此如何减小永磁电机齿槽转矩和转动惯量是高性能永磁电机设计和制造中必须考虑和解决的关键问题。

本文以一台额定功率为7.5 kW(8极、30槽)的内置式永磁同步电动机为例，从电机转子结构设计出发，首先根据所推导出的削弱齿槽转矩解析表达式，提出了采取添加辅助槽的方法来降低齿槽转矩。然后采用转子轭部凿空的方法降低转动惯量。最后采用有限元法对上述方法的有效性进行了验证。分析结果表明:本文提出的采取辅助槽的方法对原有的齿槽转矩谐波有较好的削弱作用，能较好地减少齿槽转矩，同时采用转子轭部凿空方法能较大减小电机的转动惯量，从而验证了此种转子结构的优越性。

1 转子结构优化设计

1.1 削弱齿槽转矩

1.1.1 齿槽转矩分析

齿槽转矩是永磁电机绕组不通电时永磁体与铁心之间相互作用产生的转矩。当定转子间存在相对运动时，处于永磁体极弧部分的电枢齿与永磁体间的磁导基本不变，因此这些电枢齿周围的磁场也基本不变。而与永磁体两侧面对应的由一个或两个电枢齿所构成的一小段区域内，磁导变化大，引起磁场储能变化，从而产生齿槽转矩。齿槽转矩定义为电机不通电时的磁场能量W相对于转子位置角θ的负导数，即

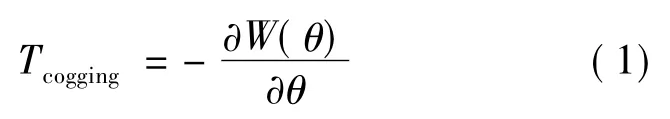
假设p对永磁磁极均匀地分布于转子轭部中，转子磁极中心位置相对于坐标原点的角度是θ，永磁电机磁动势可用傅里叶级数表示:

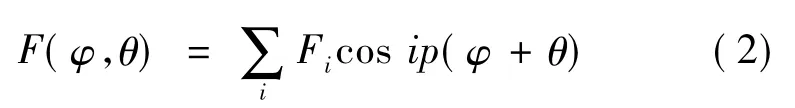
式中:i是磁动势的谐波次数，φ=ωt。磁动势方程的平方可用下式表示:

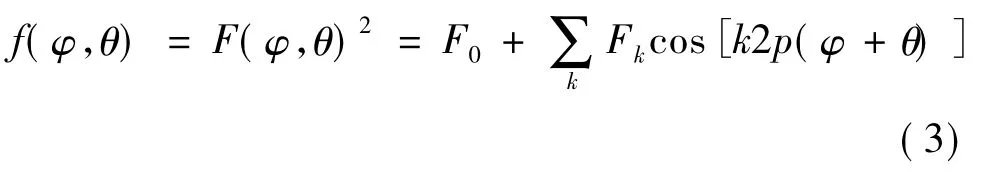
式中:F0为场函数的常量;Fk为场函数k次谐波的幅值。

气隙磁导分布可由磁导方程表示，用傅里叶级数表达如下:

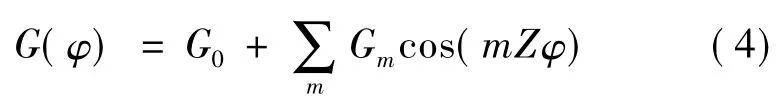
式中:G0为磁导方程的常量;Z为定子槽数;Gm为m次谐波的幅值。电机储存的磁场能量可用下式表示:

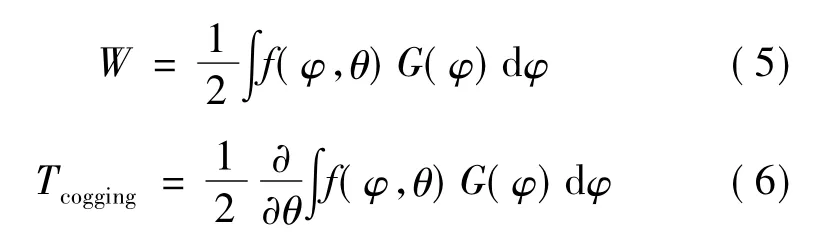
即:

2.3 各序列对各级软骨损伤的诊断能力 Fiesta-c对软骨损伤分级诊断的灵敏度、特异度、Kappa值分别为95.96%、96.41%、0.892，优于MERGE序列或FS-3D-SPGR序列，见图1～3，组间Kappa值经U检验，差异有统计学意义(P<0.05)。各序列诊断各级软骨损伤的准确度、灵敏度、特异度、Kappa值见表5。

齿槽转矩的k次谐波幅值如下:

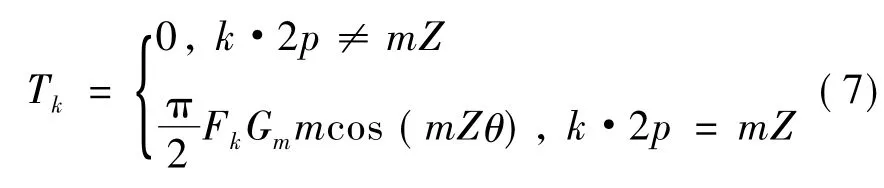
齿槽转矩是场函数和磁动势函数相互作用的结果。场函数中引起齿槽转矩的谐波频率为:

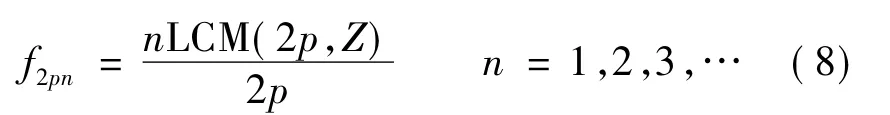
式中:LCM(2P，Z)表示槽数Z与2p的最小公倍数。当n=1时，谐波最低频率:

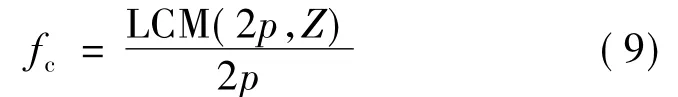
1.1.2 辅助槽削弱齿槽转矩的方法

为了削弱齿槽转矩，将场函数中引起齿槽转矩的谐波成分去掉。本文采用在永磁磁极极面上挖一些辅助槽的方法来去掉这些谐波。添加了辅助槽的永磁磁极的场函数可用傅里叶级数表示，由式(3)展开可得［2］:

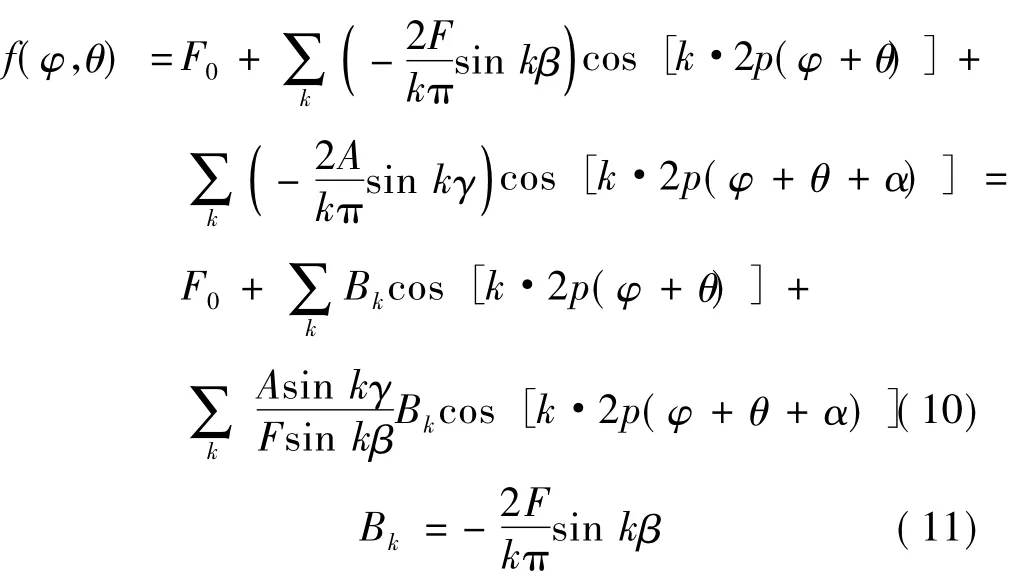
式中:F为未加辅助槽时单位角度下的气隙体积;A为添加辅助槽后单位角度下的气隙体积;β为定子槽宽的一半;α、γ分别为辅助槽的位置和宽度。式(10)右边第二项是未加辅助槽时的谐波，第三项是辅助槽所产生的谐波，两项相加就抵消了场函数中的谐波含量。要移除fc，就必须满足下式:

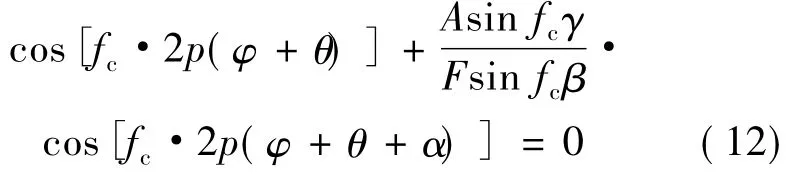
为了保持永磁电机的高转矩密度，通常永磁磁极上的辅助槽不能太深，宽度也应尽可能得小。所以本文中分析的辅助槽宽度范围为kγ＜2π，位置α为每一磁极极面中心，式(12)的解如下:

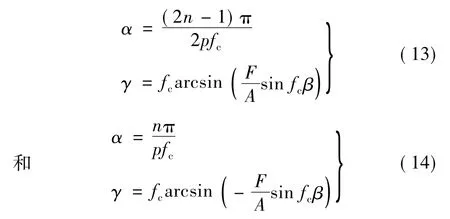
因此，可以得到满足式(12)的所有解，选择最优辅助槽的位置α和宽度γ。

本文选择辅助槽的宽度γ以及深度δ作为减少齿槽转矩的设计参数，位置α为每一磁极极面中心，原始模型和设计模型如图1所示。

图1 内置式永磁电机转子设计模型

1.2 减小转动惯量

图2给出的是该永磁同步电动机完整的磁力线分布。可以看出，转子铁心轭部近轴处平均磁密比较低，磁场分布主要集中在靠近永磁体附近。

1.2.2 转子轭部凿空方法

基于上述分析，根据转子轭部磁力线的分布情况，在尽量不改变原有磁场分布，将转子内部磁场很弱的区域部分凿空，转子轭部凿空后的电机1/4模型如图3所示。这样在不影响电机本身性能的基础上，不仅改善了转子内部的磁场分布，提高了永磁体的利用率，而且减小了电机的转动惯量，同时节约了材料，改善了电机的动态特性，使转子结构得到优化。

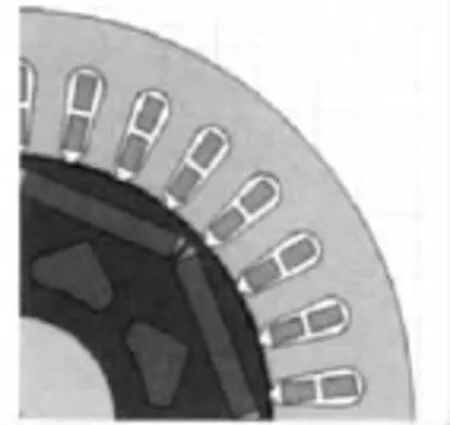
图3 转子轭部凿空后1/4模型

2 设计实例及有限元仿真

为了验证上述设计方法，设计了一台额定功率为7.5 kW(8极、30槽)的永磁同步电动机，并进行二维场的有限元分析，设计电机的主要参数如表1所示。

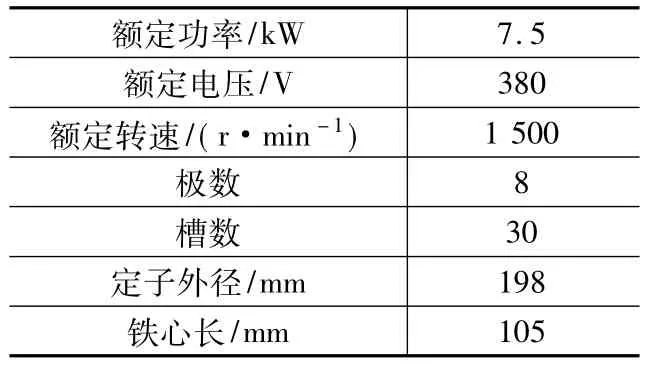
表1 电机主要参数

2.1 辅助槽有限元分析

电机有限元模型中，在永磁磁极极面上挖一些辅助槽，通过改变辅助槽的宽度γ和深度δ，达到减小齿槽转矩的目的，如图4所示。

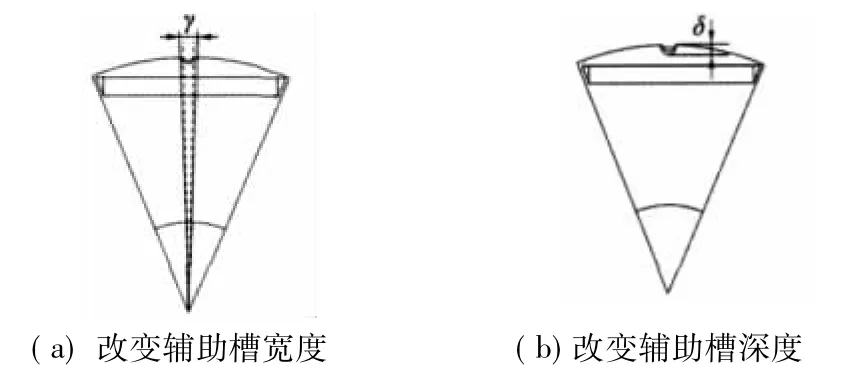
图4 辅助槽的设计参数

在辅助槽深度δ=1 mm、不同的宽度γ值条件下齿槽转矩的有限元对比如图5所示，可以看出，当δ=1 mm，γ =3.5°时，齿槽转矩最小。

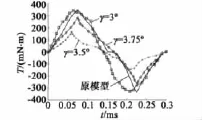
图5 不同γ值齿槽转矩对比(δ=1 mm)

在辅助槽宽度γ=3.5°、不同的深度δ值条件下齿槽转矩的有限元对比如图6所示，可以看出，当γ =3.5°，δ=1 mm 时，齿槽转矩最小。

采用辅助槽(γ =3.5°，δ=1 mm)前后齿槽转矩的有限元对比如图7所示。原模型的齿槽转矩最大值为350.56 mN·m，而采用辅助槽的齿槽转矩最大值为165.91 mN·m，为原来的47.33%，可见有辅助槽极大削弱了齿槽转矩。

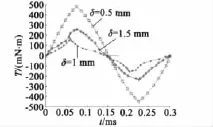
图6 不同δ值齿槽转矩对比(γ=3.5°)

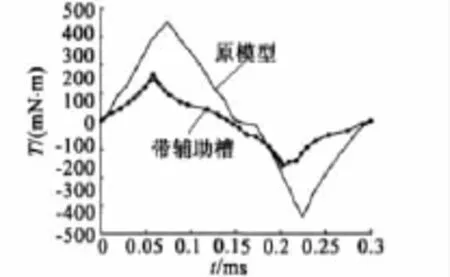
图7 采用辅助槽前后齿槽转矩对比

2.2 转子轭部凿空有限元分析

2.2.1 转动惯量计算

转子凿空前电机转子转动惯量为0.020 524 5 kg·m2，而转子凿空后的转动惯量为0.019 041 4 kg·m2，减小了 7.23%。

2.2.2 空载磁场分布分析

转子凿空后转子磁场分布如图8所示，从图中可以看出，与凿空前相比磁力线分布变化不大，分析表明转子凿空部分形状和大小适合，对永磁电机的磁路没有产生不良影响。

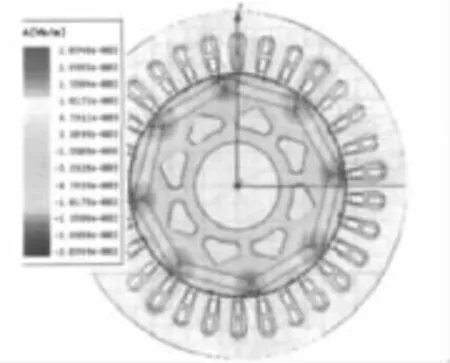
图8 转子轭部凿空后磁场分布

2.2.3 空载电动势对比分析

转子凿空前后的A相空载电动势如图9所示，其有效值分别为205.79 V和205.53 V，几乎没有变化，表明该处理对电机的空载磁场几乎没有影响。

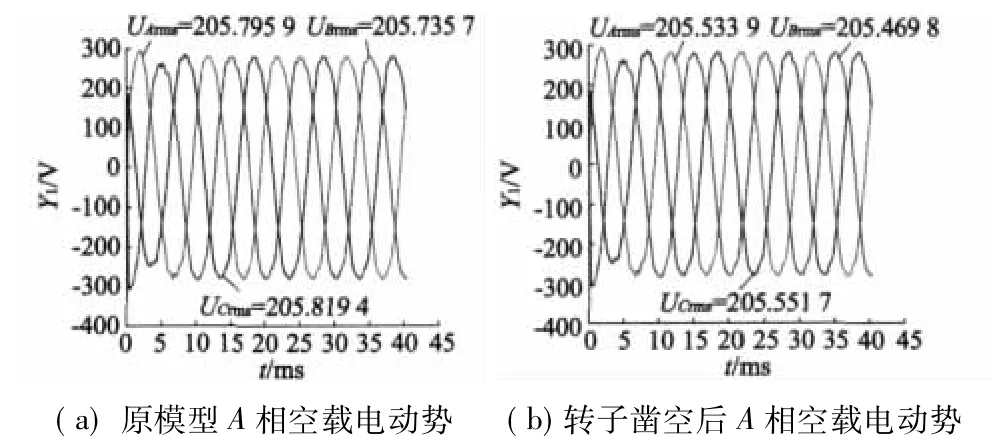
图9 转子凿空前后的A相空载电动势

3 结 语

本文以减小永磁同步电机齿槽转矩和转动惯量为出发点，通过对永磁电机的齿槽转矩数学模型和空载轭部磁场进行分析，提出采用辅助槽削弱齿槽转矩的方法，同时采用转子轭部凿空的方法来优化电机转子结构，然后以一台7.5 kW的永磁同步电机为例，运用Ansoft软件对该电机模型进行有限元分析。分析结果表明，本文所设计的转子结构比一般永磁电机的转子结构性能优越。

［1]Kioumarsi A，Moallem M，Fahimi B.Mitigation of Torque Ripple in Interior Permanent Magnet Motors by Optimal Shape Design［J］.IEEE Trans.Magn.，2006，42(11):3706－3711.

［2]Wu L，Jin W，Ni J，et al.A Cogging Torque Reduction Method for Surface Mounted Permanent Magnet Motor［C］//ICEMS Conference on Electrical Machine and Systems.2007:769－773.

［3]Kang G H，Son Y D，Kim G T，et al.A Novel Cogging Torque Reduction Method for Interior－Type Permanent－Magnet Motor［J］.IEEE Trans.Magn.，2009，45(1):161－167.

［4]唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，2007.

［5]王秀和.永磁电机［M］.北京:中国电力出版，2007.