基于互模糊函数的快速时差频差联合估计

王奉帅，刘聪锋，张 亚，甘 昶

(1.西安电子科技大学，电子对抗研究所，西安 710071;2.解放军73677部队，南京 210016)

0 引言

互模糊函数计算被认为是对时差频差联合估计的基础，在相当多的应用中，要求的准确性需要对很长的数据进行积分，这就对数据的实时处理造成了困难[1]。互模糊函数在很多领域具有重要的应用，如雷达、声纳、医学成像及语音分析等方面。为了计算模糊函数，经常用到有限模糊函数，将利用互模糊函数来估计时差频差。

在大多数情况下，由于目标与接收器之间存在相对运动，接收器之间接收到的信号既存在TDOA(到达时间差)，也存在由相对运动引起的FDOA(到达频率差)，因此不能单纯的计算其中任何一个参数。互模糊函数是计算信号TDOA和FDOA的基本测量算法，很多算法已经用来计算窄带信号的互模糊函数，这些算法在结构上有很多共同点(如抽取、滤波等)。这些算法的一个应用就是对辐射源定位，定位算法根据信号的TDOA和/或FDOA计算出目标的位置。在辐射源定位中，目的是尽可能快的计算互模糊函数，并利用计算出来的结果来确定目标的位置[2]。

由于采样点数很多，互模糊函数又可以看成是时差和频差的两维相关，因此计算量巨大，为此如何降低其运算量成为一个研究热点[3～5]。仔细观察互模糊函数的计算公式，可以看出，针对每一个延迟单元，计算参考信号与延迟信号内积的快速傅里叶变换，保存变换后的最大幅度值以及对应的频率，然后在这些最大之中进行一维搜索，搜索到的最大值所对应的延迟值就是接收信号之间的TDOA，对应的频率就是接收信号之间的FDOA，但是，采样频率一般远远大于多普勒频差，所以计算的很多频率点不在期望的频率范围内，因此需要更好的算法来计算互模糊函数。从这几种算法中可以看出，计算互模糊函数需要的先验知识为信号的最大延迟时间以及最小延迟时间。

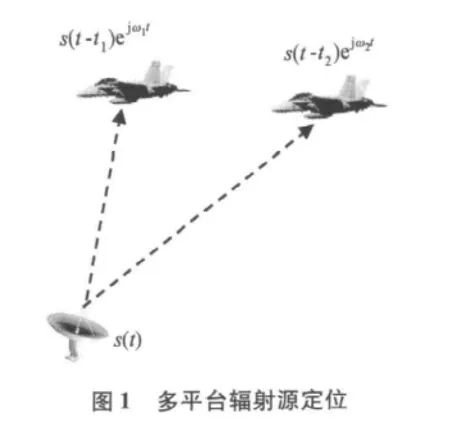
1 互模糊函数时差频差联合估计原理

辐射源发射的信号用s(t)表示，用飞机表示的接收器接收信号，每一个接收器与辐射源有一段特定的距离，因为辐射源的准确位置未知，所以各接收器到辐射源的距离也是未知的。辐射源在某时刻t发射信号，因为接收器到辐射源之间存在一定距离，发射的信号经过一段时间到达接收器，接收到的信号是发射信号的延时形式。假设辐射源是固定的，接收器运动是的，根据多普勒效应，接收到的信号跟源信号相差一个多普勒频移，多平台辐射源定位，如图1所示。在图1中，两个接收信号从左到右，包括时间延迟和多普勒频移为 s(t－t1)ejω1t，s(tt2)ejω2t，其中 t1，t2表示时间延迟，ω1，ω2表示接收信号相对源信号的多普勒频移[2]。因为信号的发射时间及载频是未知的，无法求出到达接收机处的t1，t2，ω1，ω2，但是应用互模糊函数可以将两接收器接收到信号之间的时差频差估计出来。二维向量互相关示意图，如图2所示。

如图2所示的二维矢量，假设要求出θd，其中一种方法是固定V1，顺时针旋转V2一个角度增量θ，对于每一个θ值，计算两向量的内积如下

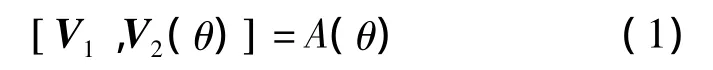
这就变成了一个θ的函数。当θ的值等于θd时，A(θ)达到最大值。

令

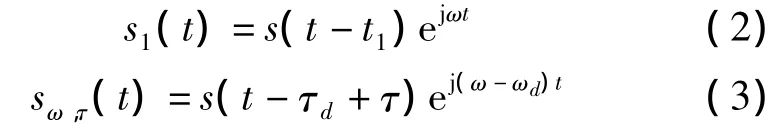
式(3)为τ和ω的函数。将上面的方法应用到接收到的两信号中可以得到

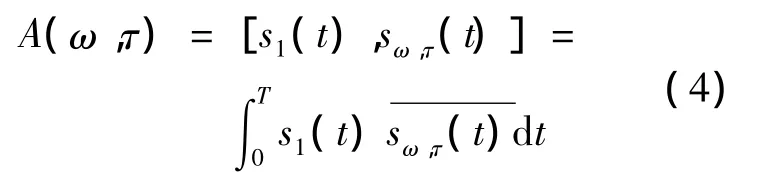
将式(3)带入式(4)并取共轭可以得到

由式(5)可以看出，当τ=τd且ω=ωd时，两信号的内积达到最大值。

2 互模糊函数快速计算

根据实际情况，两个接收机1、2接收到的信号可以建模为

式中，s(t)为待定位辐射源发射的信号;α1，α2为衰减因子;td，fd分别为接收器2相对接收器1的时间延迟以及多普勒频率差;n1(t)，n2(t)为互不相关的高斯白噪声[6]。

令

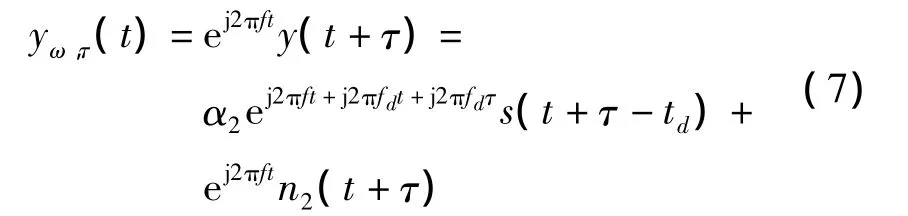
根据式(5)可以得到接收信号的互模糊函数为

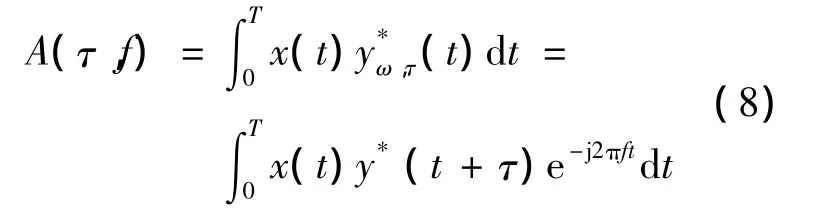
式中，T为积分上限;理论上τ的最大值等于两接收器之间的直线距离R除以光速c。而且从式(8)可以看出，求两信号的互模糊函数实际上是对x(t)和y*(t+τ)之积做傅里叶变换。

可以得到式(8)的离散形式为

如果接收信号的采样频率为fs，则离散时间点为 t=nTs=n/fs，n=0，1，2，3…，N －1，若总的采样时间长度为T，则采样点数为N=Tfs，时间延迟为τ =k/fs，频率延迟为 f= νfs。

2.1 互模糊函数的离散傅里叶计算形式

上面介绍了信号模型，以及计算时差频差的互模糊函数，如果令

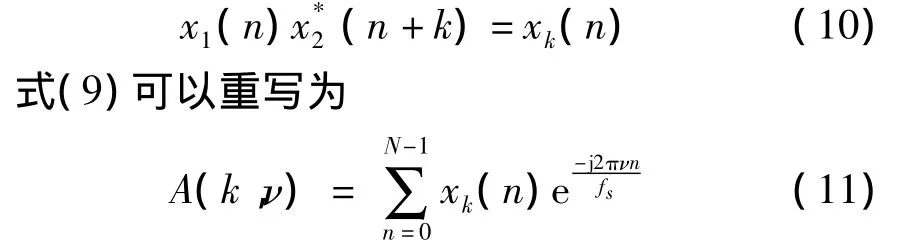
可以看出，式(11)其实就是计算两信号内积的离散傅里叶变换。对每一次时延做一次离散傅里叶变换，搜索出最大值所对应的频率值，然后对Rfs/c个频率值中找出一个最大值，所对应的序号为信号的时延值。R为两个接收器之间的直线距离。

2.2 互模糊函数的简化计算形式

当计算式(11)时，离散傅里叶变换的频域范围为(－fs/2，fs/2)，但是，实际中信号的多普勒频移ν＜＜fs，所以根据式(11)计算的大部分频率点不在期望的频率范围内。因此，需要一种更有效的方法来计算式(11)。首先简化式(11)，令n=mL+p，m=0…M－1，p=0…L－1，为了保证产生 M个模块，x(n)的长度必须能被L整除，如果不能整除可以补零。这样式(11)就可以写为

从式(18)可以看出，计算量比式(11)减小了L倍。

3 仿真结果分析

仿真用到的信号形式及参数，见表1。

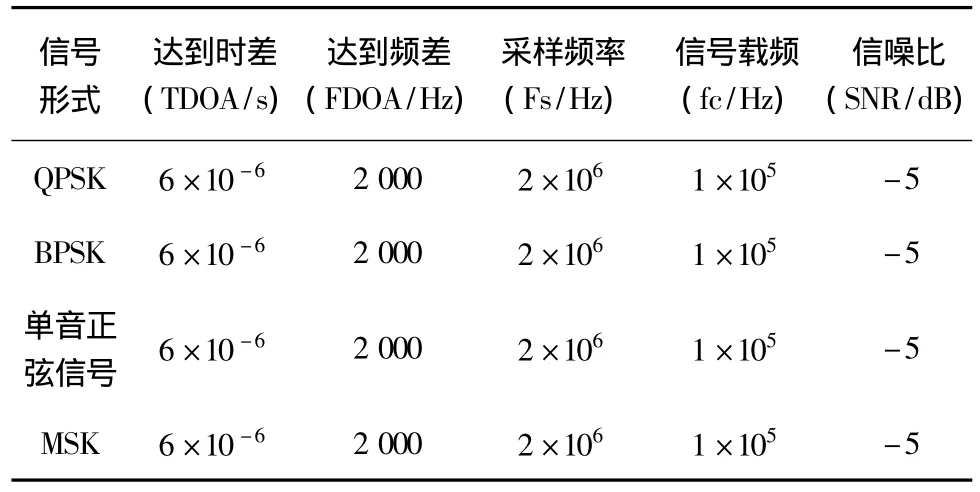
表1 信号形式及参数

在不同的采样点数下，分别利用两种方法对表一中的信号进行时差频差联合估计，可以得到频差估计误差曲线，如图3所示，时差估计误差曲线，如图4所示，对应的计算时间，如图5所示。

由图3可以看出，在采样点数相等的情况下，传统时差频差联合估计的到达频差估计精度要高于简化后的算法，而且随着采样点数的增加，两种算法的精度都在提高，精度差距越来越小。

由图4可以看出，在采样点数相等的情况下，传统时差频差联合估计与简化后的算法都能够精确的估计出到达信号的时差。

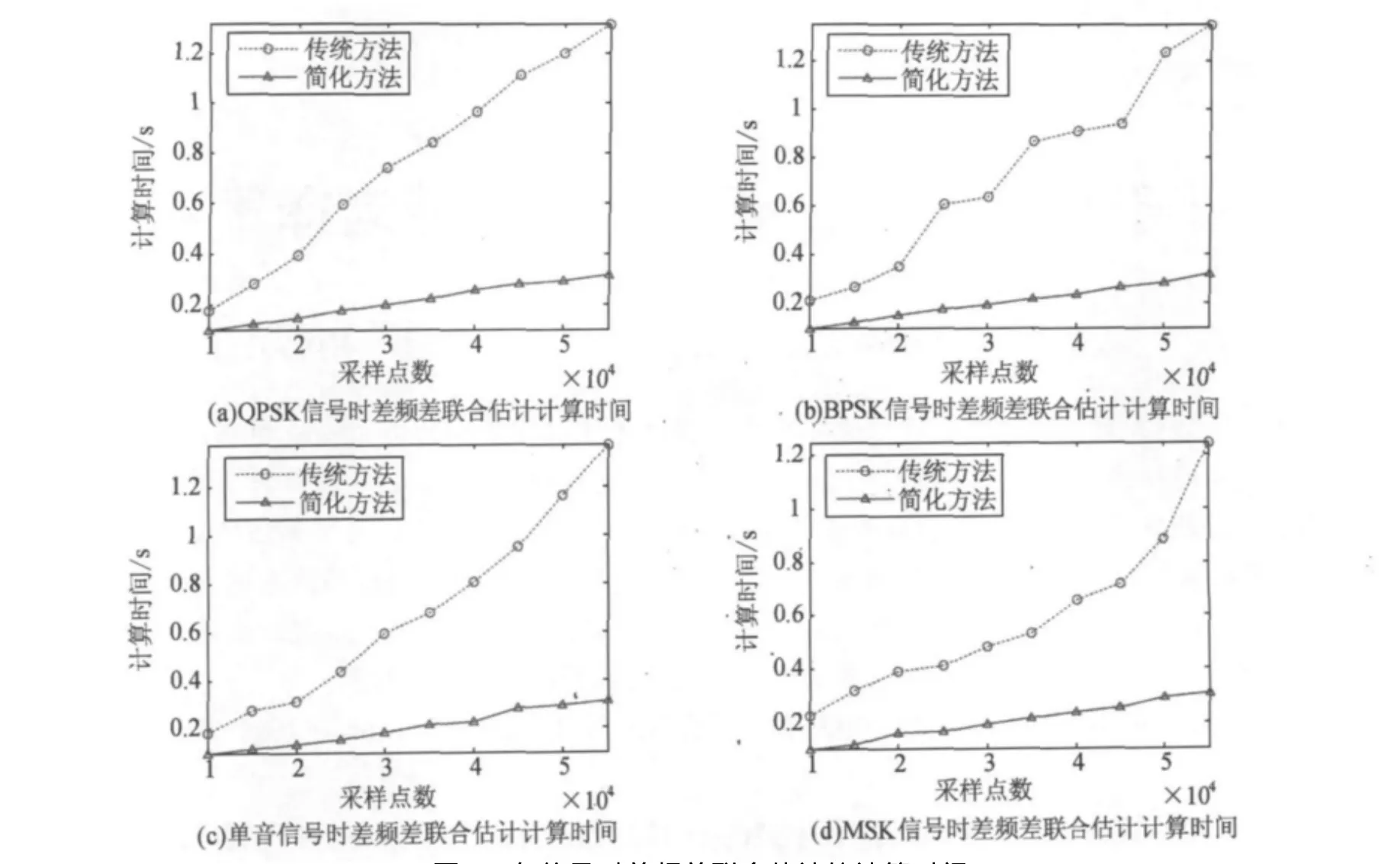
图5 各信号时差频差联合估计的计算时间

由图5可以看出，在采样点数相等的情况下，传统时差频差联合估计的频差估计消耗的时间远远大于简化后的算法，随着采样点数的增加，两种算法的计算时间虽然都有增加，但是简化后的算法计算效率明显优于传统的时差频差联合估计算法。

所以，如果提高简化算法的计算精度，可以增加采样点数，综合考虑精度与计算时间，简化后的算法优于传统算法。

4 结语

传统的利用互模糊函数进行时差频差联合估计，需要在一定的时差和频差范围内搜索最大值，在时差和频差范围已知的情况下，缩小搜索范围可以减少计算量，但是当它们未知时就需要搜索很大范围，这样不能保证实时估计参量。利用离散傅里叶变换，在满足采样定律的前提下，采样频率大于两倍的多普勒频率，就能够计算出多普勒频率，虽然计算量也比较大，但是与二维搜索相比，已经减少了不少计算时间。而将两接收信号的内积分块，再对分块后的内积做快速离散傅里叶变换能进一步降低计算量。

[1]STEIN S.Algorithms for Ambiguity Function Processing[J].IEEE Transactions on Acoustics，Speech and Signal Processing，1981，29(3):588-599.

[2]CHRISTOPHER L YATRAKIS.Computing the Cross Am-biguity Function-A Review[Z].2005.

[3]OZDEMIR A K，ARIKAN O.Fast Computation of the Biguity Function and the Wigner Distribution on Arbitrary Line Segments[J].IEEE Trans on Signal Processing，2001，49(2):381-393.

[4]TAO R，ZHANG W O，CHEN E Q.Two-stage Method for Joint Time Delay and Doppler Shm Estimation[J].1ETRadar，Sonar＆Navigation，2008，2(1):71-77.

[5]朱伟强，黄培康，张朝.利用互模糊函数联合估计的双星高精度定位技术[J].系统工程与电子技术，2006，28(9):1294-1298.

[6]朱伟强，黄培康，张朝.基于互模糊函数的时差频差估计算法及实现途径[J].南京理工大学学报，2009，33(4):511-515.