短波信道时间选择性衰落特性的实验研究

鲁转侠，凡俊梅，柳 文，娄 鹏

(中国电波传播研究所青岛研发中心电波环境特性及模化技术重点实验室，山东 青岛 266107)

0 引言

短波信道是一种时变的信道。电离层的运动所引起的多普勒频移造成了短波信道的频率扩散，而信道的频率扩散则产生了接收信号频谱的扩散，即造成时间选择性衰落。描述信道时间选择性衰落特性的参数较多，但是，最常用的有信号电平幅度衰落的累积分布、衰落率、衰落深度、基本相关时间、基本不相关时间、多普勒展宽和相位起伏等，它们对利用短波信道工作的探测系统设计是特别有意义的。

早在20世纪30年代Ratcliffe等人就开展了有关于电离层传播信号衰落特性的研究[1];许多学者已对垂直探测路径上的电离层衰落特性进行了大量研究[2～4];1965年至20世纪80年代中期，中国电波传播研究所利用短波授时台信号及国际通信电台信号在大圆距离(范围为700～19602 km)不等的多条电路上进行了短波信道时间选择性衰落测试实验[5]，但未进行分模式统计分析，其结果体现的是混合模式下的整体特性。1995年宁百齐等人[6]对混合模式下短波一跳天波多普勒频移和展宽开展了研究;近年来，凡俊梅等学者分析了不同传播模式电波信号的衰落特性[7～9]，研究结果表明1000 km左右单程电路单跳模式的时域信号幅度衰落并非瑞利分布，亦非正态分布，但频域信号幅度衰落满足正态分布。

以上研究证明，对于收发固定的短波斜向探测电路，即使工作频率相同，同一种传播模式在不同电离层状态下的衰落特性也不相同;而同一电离层条件下，不同传播模式信号的衰落特性也存在较大差异。

本文在以上研究的基础上对短波信道的时间选择性衰落特性开展了进一步的研究，具体分析了六个常用于描述短波信道时间选择性衰落特性的参数:信号电平幅度衰落的累积分布、衰落深度、衰落率、基本相关时间、基本不相关时间和多普勒展宽。

本文针对一组电离层稳定状态下的试验数据还进行了不同积累时间积累效果(频谱)的分析。

1 试验情况及理论分析

1.1 试验情况

2009年12月本课题组对大圆距离约770 km的斜向探测电路的电离层传播模式特性的变化进行了观测。试验方法为先扫频探测，获取固定电路的电离层传播模式状态信息，然后进行长时间固定频点的连续观测。信号形式有调频信号和编码信号两种，每帧输出为经匹配滤波器处理之后的探测结果。扫频探测数据可为定频探测频谱上传播模式的识别提供重要参考，定频探测数据不只可获得固定频点不同传播模式的频谱信息，还能够获取不同传播模式的幅度和相位信息。

1.2 理论分析

(1)幅度衰落的累积分布

短波信道中可用初等函数来表示的幅度衰落分布，有[10，11]:瑞利分布、正态分布、威布尔分布、极值分布及指数分布等，其概率密度函数分别为:

a)瑞利分布

其中η(大于0)为尺度参数;γ为位置参数;β为形状参数。威布尔分布是一种具有广泛通用性的分布概型，指数、瑞利、正态等分布均为威布尔分布中的特例。

(2)衰落深度

通常定义累积分布曲线上90%与10%两点之间所对应的信号电平之差为衰落深度，其可充分地反映信号幅度衰落变化的范围。衰落深度与电路距离、电路地理位置、工作频率和工作时间等因素有关。

(3)衰落率

衰落率是描述信号电平变化快慢的参量，通常定义单位时间内以正(或负)斜率越过中值电平的次数为衰落率。像衰落深度一样，衰落率与电路距离、地理位置、工作时间和工作频率有密切的关系。

(4)基本相关时间及不相关时间

幅度衰落的自相关分析能较好地反映信号电平随时间变化的关联程度。

若用S( t)代表信号幅度随时间变化的函数，那么信号幅度衰落的自相关函数可用R(τ)表示，其由下述关系式确定:

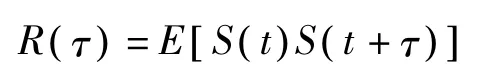
信号幅度间线性联系的密切程度可用相关系数描述，其表达式为

式中，mS(t)为信号幅度序列均值。

通常，称对应于 ρ( τ1)=0.9的时间 τ1为“基本相关时间”，而称对应于 ρ( τ2)=1/e的时间 τ2为“基本不相关时间”，ρ( τM)=0.5所对应的时间 τM为自相关半径。它们的物理意义是:在[0，τ1]时间区间的任一时间间隔上，前后两时刻的接收信号电平的衰落是基本相关的，而在[τ2，+∞)时间区间的任一时间间隔上，前后两时刻的接收信号电平的衰落是基本不相关的。

(5)多普勒展宽

多普勒展宽即信道的频率扩散量，它是反映信道频率色散的重要参量。从理论上讲，信号的多普勒展宽与衰落率成正比，并与基本不相关时间成反比。因此，当测得信道的时间选择性衰落的幅度分布和相关特性时，可用衰落率或基本不相关时间等统计参数来对多普勒展宽参数进行理论估计。

2 试验数据分析及结果

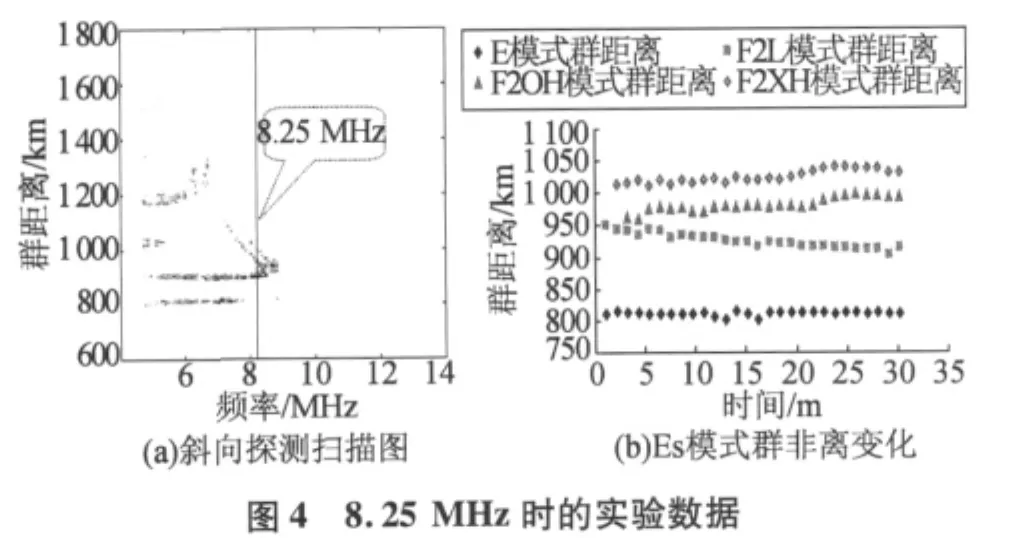
本文对此次试验的11组不同频率(4～13 MHz)、不同时间(11:00～19:00)的定频试验数据进行了不同传播模式(E(Es)、F2L、F2OH和F2XH)的时间选择性衰落特性分析。考虑到时域(匹配滤波后的结果)和频域(对某段时间上的样本频谱分析的结果)不同的信号特性，选取了4组群距离变化较稳定的实验数据(如图1～图4所示)从时域进行统计。频域信号提取时，定义最小信噪比为10 dB。时域信号提取时，首先在频谱图上搜寻每个传播模式信号最强的点所在的距离门，然后在时域不同脉冲上提取出该距离门对应的信号幅度。

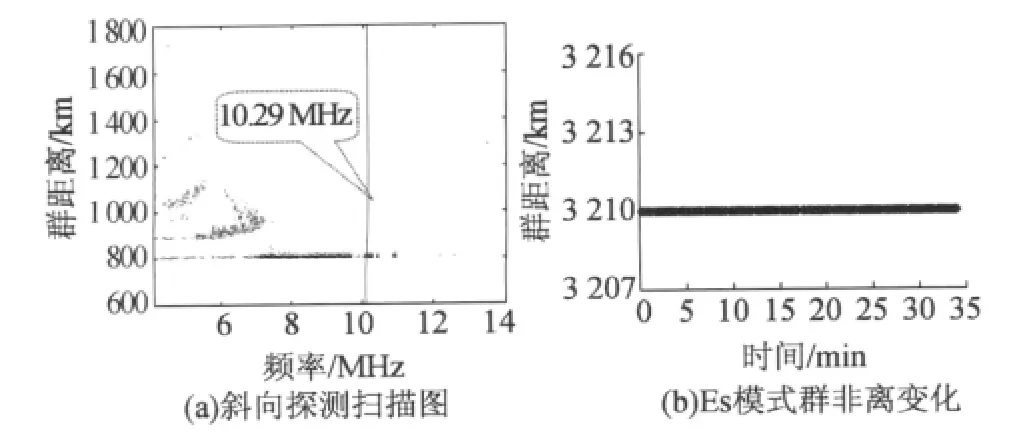
图1 10.29 MHz时的实验数据

(1)幅度衰落累积分布特性的分析

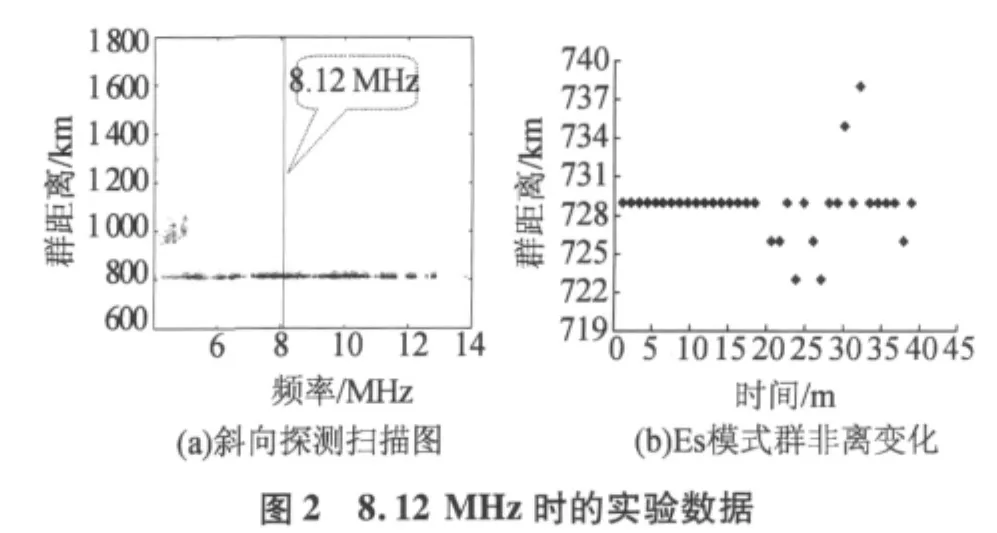
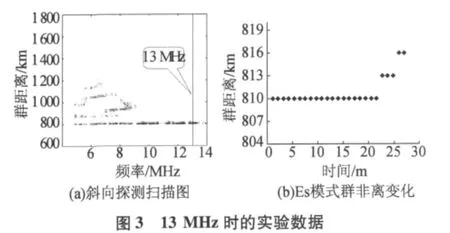
多普勒域(频域)体现的是较长时间的积累效果;时域则不同，是短时的变化特性。因此二者的幅度衰落特性也不尽相同。本文从多普勒域和时域两方面考虑，结合以上五种分布类型，分析了不同传播模式信号的幅度衰落特性。此次试验数据的幅度衰落累积分布特性分析结果，见表1。

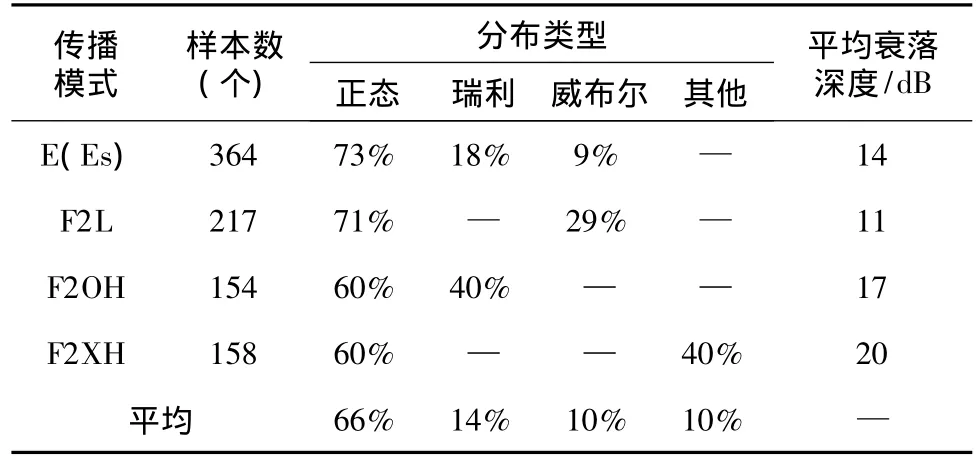
表1 多普勒域不同模式信号幅度累积分布及幅度分布的平均衰落深度

(2)衰落深度和衰落率的分析

衰落深度和衰落率可充分地反映信号幅度衰落变化的范围及快慢。此次试验数据的衰落深度和衰落率分析结果，见表2。

表2 时域不同模式信号幅度累积分布及幅度分布的平均衰落深度、衰落率

(3)基本相关时间及不相关时间的分析

幅度衰落的自相关分析能较好地反映信号电平随时间变化的关联程度。此次试验数据的基本相关时间及不相关时间分析结果，见表3。

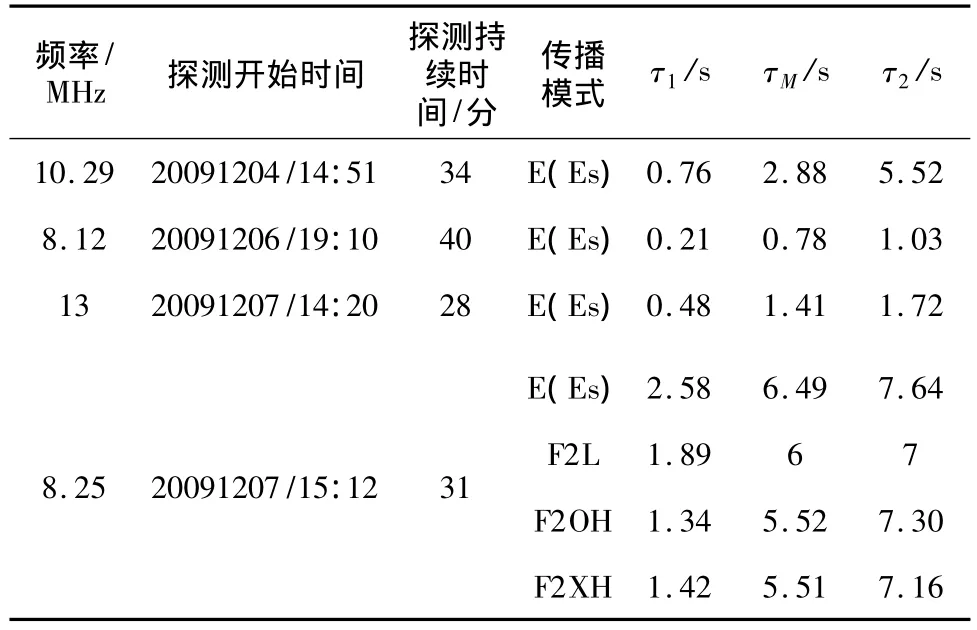
表3 不同模式幅度衰落自相关的特征值

(4)多普勒展宽的分析

分析时，首先对匹配滤波后的数据用FFT算法进行多普勒谱分析，其获得频谱的多普勒分辨率为0.0186 Hz，时间分辨率为54 s;然后，多普勒展宽D按传统的均方根宽度定义[11]测量，其中心代表平均的多普勒频移，表达式为

式中，Bi为频谱的幅度值，它对应的频移用fi表示;是平均的多普勒频移，表达式为

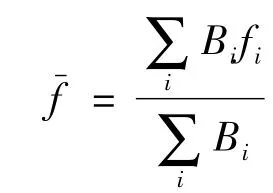
此次试验数据多普勒展宽及多普勒展宽的变化范围分析结果，见表4。

表4 不同频率、不同模式的平均多普勒展宽

(5)不同积累时间频谱的分析

对匹配滤波后的数据采用FFT算法分析获得的多普勒谱与电离层状态、传播模式及积累时间等因素有关。这里定义频谱图上峰值以下4 dB处无多峰现象就为电离层有效积累，对应的积累时间为有效积累时间。本文对这次试验数据进行了电离层有效积累时间的分析，其中，E(Es)模式最短的有效积累时间约为20 s，电离层状态较稳定时可达6 min左右(如8.25 MHz定频数据E(Es)模式，如图5～图7所示，图中虚线为峰值以下4 dB位置)。由于试验期间F层传播模式群距离变化均较快，根据统计分析结果，无法给出关于有效积累时间的定量描述。

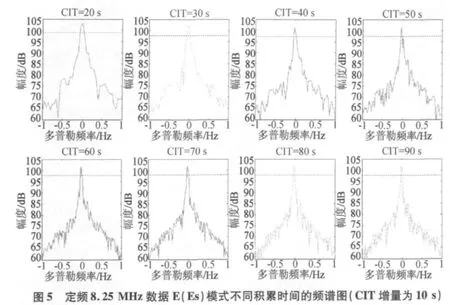
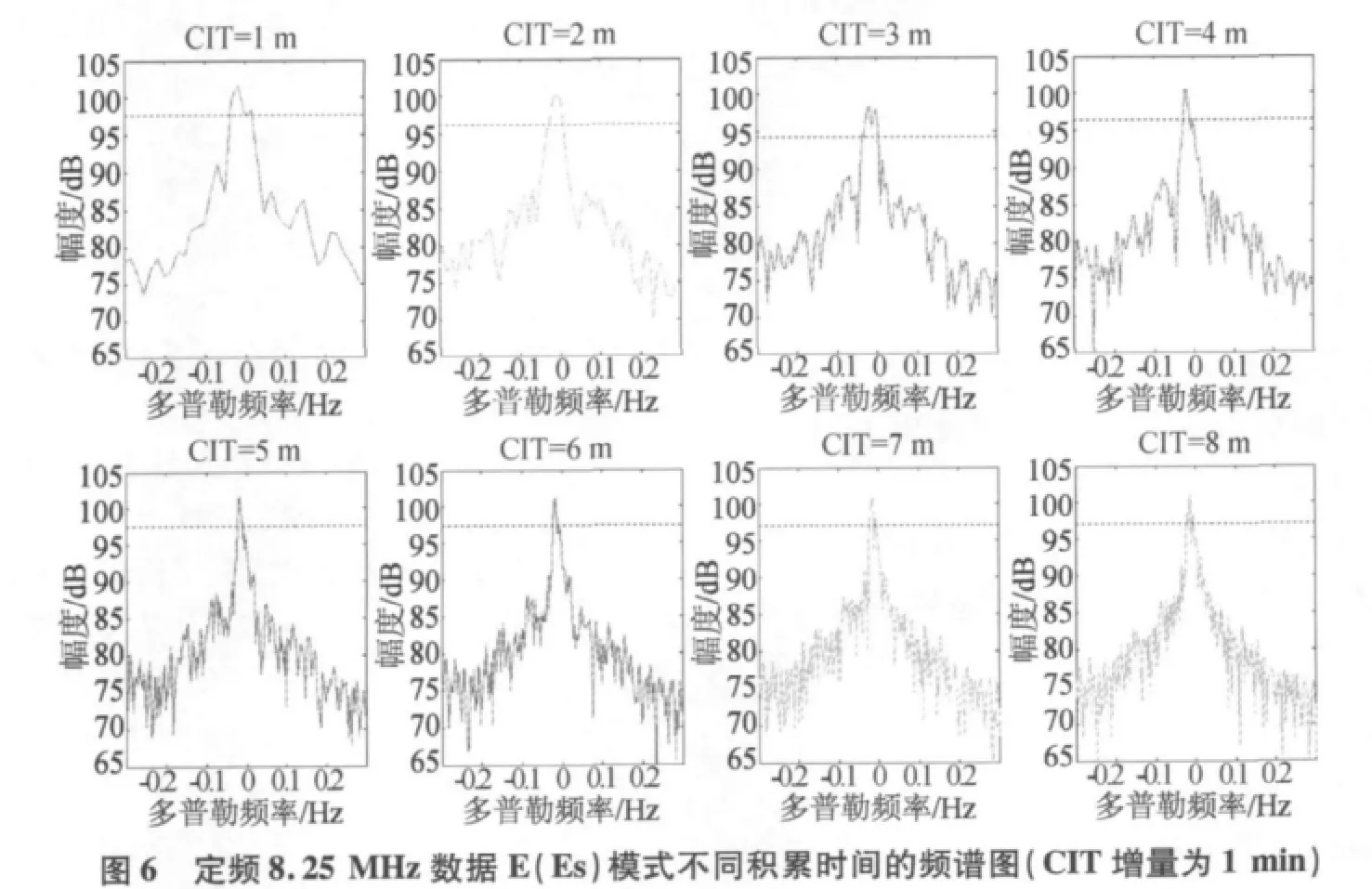
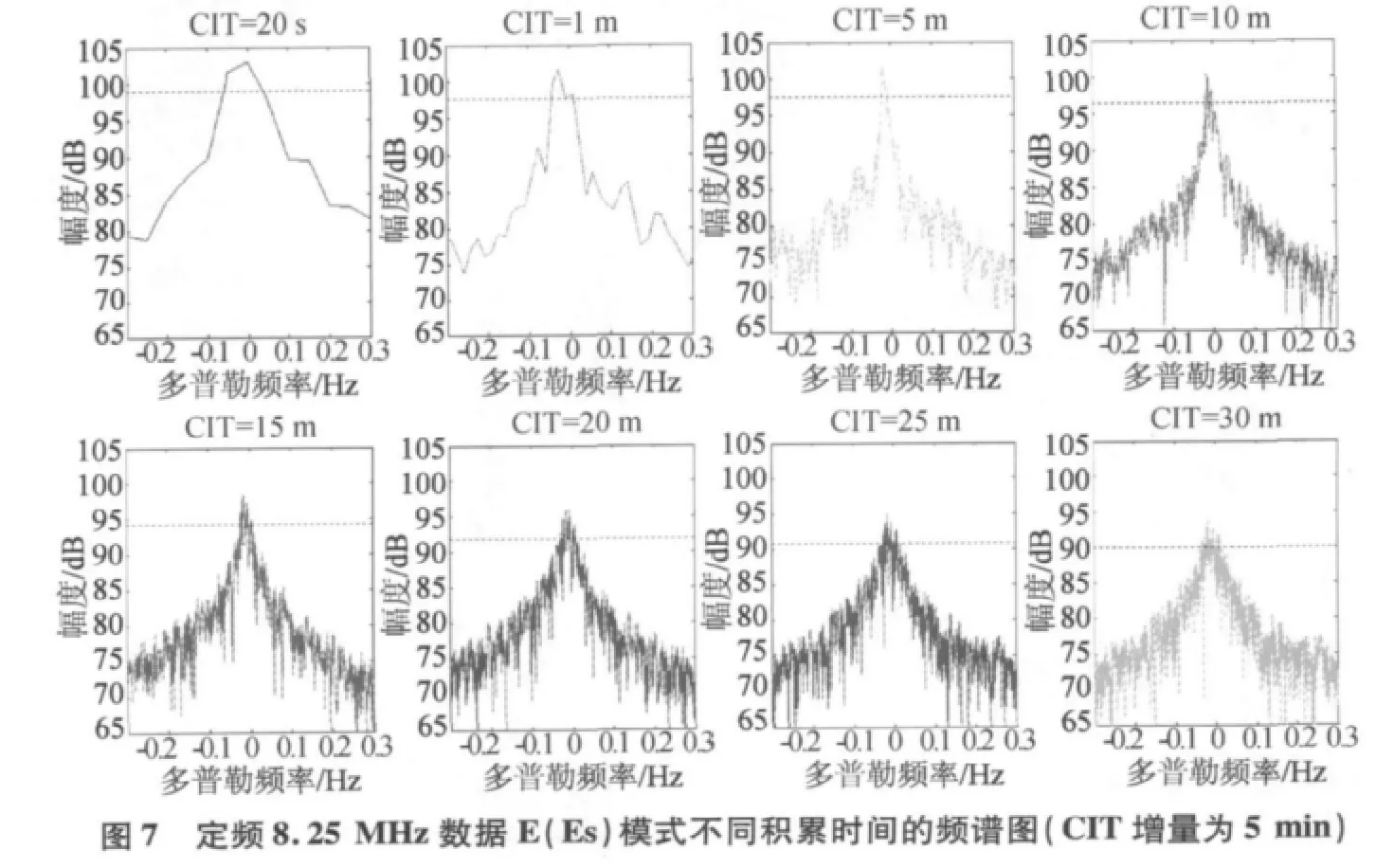
为了进行不同积累时间下的信号幅度比较，这里利用不同积累时间的积累点数对积累后的频谱进行了归一化。对8.25 MHz定频数据E(Es)模式的不同积累时间下幅度的分析结果，如图8所示，归一化后幅度整体趋势上减小。

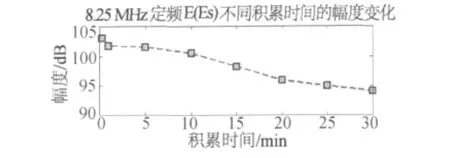
图8 E(Es)模式不同积累时间信号幅度的变化

3 结语

稳定的电离层状态是利用短波信道工作的系统实施有效探测的重要条件。通过以上试验数据的分析，可获得如下对后继工作具有参考意义的结论。

(1)幅度衰落特性

不同传播模式，多普勒域幅度衰落66%较为符合正态分布(见表1)，时域幅度衰落73%较为符合维布尔分布(见表2)。

(2)衰落深度和衰落率

多普勒域F2层低角模式的衰落深度小于E(Es)模式，但均达10 dB以上。

时域E(Es)模式衰落深度均达10 dB以上;所选8.25 MHz定频数据F2层在等时间间隔的短时样本中，高角的衰落深度远小于低角;F2层低角模式衰落率小于E(Es)模式，F2层高角模式衰落率最大。

(3)基本相关时间及不相关时间

8.25MHz定频探测数据E(Es)模式的基本相关时间最长，约达3 min，基本不相关时间和自相关半径也最长，而且自相关半径较为接近基本不相关时间，这主要是由于此组数据衰落率较小、电离层较稳定的原因。

(4)多普勒展宽

E(Es)模式和F2层低角模式的多普勒展宽及变化范围没有明显的大小之分，但二者基本都大于F2层高角。

(5)不同积累时间积累效果

有效积累时间:不同电离层状态下，其有效积累时间也不同，此次试验最长的有效积累时间约为6 min，最短的只有不到20 s，甚至更短。

积累效果:有效积累时间内，积累时间越长，多普勒分辨力越高，信号更加锐化，峰值以下4 dB展宽越小;积累时间大于有效积累时间时，相干性变差，出现明显的多峰现象，随着积累时间增长，多峰现象加重，积累效果恶化。

幅度:随着积累时间增长，归化后幅度大多数趋势上呈整体减小，这与电离层信道状态和相关性有关。

(6)探测频率的选择

本次试验较低频率(如 4.365 MHz、4.1 MHz)的探测效果绝大多数较差，通过此次试验数据的分析，建议利用短波信道工作的系统应尽量选择模式少、稳定的较高频率。

[1]RATCLIFFE J H，PAWSEY J L.A Study of the Intensity Variations of Down Coming Wireless Waves[C].Proc Camb Phil Soc，1996 IEEE National Radar Conference，1933(29):301-318.

[2]ESSEX E A，HIBBERD F H.Frequency and Spatial Correlation of Fading Radio Exhoes From the Ionosphere[J].J Atmos Terr Phys，1968，30(5):1019-1031.

[3]ESSEX E A.Periodic Fading of Ionospheric Echoes[J].J Atmos Terr Phys，1968，30(7):1441-1443.

[4]FELGATE D G，Golley M G.Ionospheric Irregularities and Movement Observe with a Large Aerial Array[J].J Atmos Terr Phys，1971，33(9):1353-1369.

[5]戴耀森.短波数字通信自适应选频技术[M].浙江科学技术出版社，1992.

[6]宁百齐，李钧.短波一跳天波多普勒频移和展宽的变化[J].电波科学学报，1995，10(4):66-72.

[7]凡俊梅，焦培南等.电离层不同传播模式信号多普勒频移的实验研究[J].电波科学学报，2008，23(1):34-40.

[8]凡俊梅，马小村等.电离层不均匀体对短波信号影响的实验研究[J].电波科学学报，2008，23(3):443-448.

[9]凡俊梅，焦培南等.电离层不同传播模式信号衰落特性的实验研究[J].武汉大学学报，2009，55(2):244-248.

[10]张卓奎，陈慧婵.随机过程[M].西安电子科技大学出版社，2003.

[11]许承德，王勇.概率论与数理统计[M].科学出版社，2001.