基于模糊聚类的交通小区划分方法研究

刘乙霏 （上海海事大学 经济管理学院，上海 200135）

基于模糊聚类的交通小区划分方法研究

刘乙霏 （上海海事大学 经济管理学院，上海 200135）

阐述了交通小区的定义，划分交通小区的目的与原理，依据模糊聚类分析法，运用MATLAB软件进行聚类分析，提出整合方案。

交通小区；模糊聚类分析法；MATLAB

1 交通小区概念

交通小区是具有一定交通关联度和交通相似程度的节点或连线的组合，随时间、关联度和相似度的变化而变化，反映了城市道路网交通的时空变化的特性[1]。

2 交通小区划分的目的和原理

在交通规划领域中提出了划分交通小区。交通小区是指研究交通生成与分布的基本空间单位。划分交通小区是交通调查与规划中最基本的工作。其主要目的是在满足精度要求的情况下，强调交通调查的实际可操作性，尽可能减小交通调查的工作量，降低交通分析和预测的难度；交通需求量可以在交通小区的分布图上动态地显示出来，可以直观的反应交通需求分布，从而为城市道路网络的交通流提供数据，进而运用交通分配理论模拟道路网上的交通流。

交通小区的划分遵循以下原则：

·保证小区内土地利用、经济社会指标的一致性，不应打破城市行政区的划分；

·尽量将铁路、河川等天然屏障作为分区界限，避免小区内存在的自然或人为的障碍线；

·小区形状尽量为规则形状；

·应充分考虑城市道路网结构，尽可能使小区划分与道路网协调一致；

·尽可能使交通小区出行中心位于路网节点 （交叉口和干道）上；

·不以干道作为划定小区的界线，尽可能使道路两侧同在一个交通小区，以便于资料收集整理；

·划定区内的出行次数尽可能不超过全区域内出行总数的10%～15%。

3 传统交通小区划分的理论分析

从根本上讲，划分交通小区范围大小与小区数目取决于不同性质的OD调查工作所要求的精准程度。已往的交通小区划分中，主要运用目标层次分析法确定交通小区的划分。即针对不同目标层次路网的OD调查，对交通小区划分提出不同要求。

按照行政区域划分交通小区：

·为大城市和国道干线路网规划收集数据而进行的路网OD调查工作，要求调查结果反映出大型城市、首府和行政中心等节点的交通连通性时，需要将交通小区的范围设置的大些，但必须保证交通小区划分到研究目标城市的下一级城市的节点区域。如果研究区域内一些经济较为发达、交通矛盾较为突出的地区，为提高工作的精度应将小区划分的更细。

·为研究中等城市和省级道路规划收集数据而进行的路网OD调查工作，所划分交通小区的数目需要大于或等于研究区域内所有的区的数目。

·为区一级行政单位做路网规划收集数据而进行的OD调查工作，原理上应将居住小区和主要单位划分为不同的小区，实际中，这样做会增加无谓的工作量，并且得不出有效的数据，因此，交通小区的划分应以居住区和主要单位为初步方案，然后针对其中相邻，居民出行分布类似的居住区和单位进行合并。

还可以按照影响因素的不同划分交通小区。影响交通小区划分的因素如下：

·用地性质

用地性质对居民的出行特征产生直接的影响，不同的用地性质会导致不同的交通出行特点。

·交通复杂程度

交通小区如果处于研究区域内部，应在面积、人口与交通发生量与吸引量之间保持适当的均匀性；交通小区如果处于研究区域外部，应随着与对象区域距离的加大，逐渐增大交通小区的规模，以减少不必要的工作量。

·自然地貌

在一般情况下，山川等自然障碍物被作为行政区划分界线使用，因此这与第一条并不矛盾。

4 模糊聚类分析法原理及步骤

聚类分析方法是由传统的分析方法拓展出来，是按照特定要求对事物进行分类的数学方法。实际生活中，要解决的问题往往具有模糊性。一个事物是否属于某一类、一组事物是否能并为一类等问题不是那么泾渭分明的，不能明确回答 “是”或“否”，这是一个隶属程度的问题，即只能做出 “某种程度上是或不是”的回答，这就是模糊聚类分析。

模糊聚类是采用模糊数学方法，依据客观事物间的特征、亲疏程度和相似性，通过建立模糊相似关系对客观事物进行分类的一门多元技术。本文运用模糊聚类分析法对某一行政区路网规划中的交通小区初步方案进行合并，以期得到更合理的交通小区划分结果。

模糊聚类分析法的计算过程如下：

STEP1：指标选择

本文选择经济社会和交通运输方面以下指标作为交通小区划分的决定因素：人均收入、容积率、地块面积、产业结构系数、路网面积密度、百人机动车保有量。

STEP2：数据标准化

首先对原始数据进行标准化处理，设域U=｛u1,u2,u3,u4,u5,u6｝为被分类的对象，其中，u1,u2,u3,u4,u5,u6分别表示人均收入、容积率、地块面积、产业结构系数、路网面积密度、百人机动车保有量。由于原始数据不在［0,1 ］区间，故需对其进行标准化计算。

标准化计算公式为：

将各种标准化值进行数值归一化，使其转化到［0,1 ］内。公式为：

STEP3：建立模糊相似矩阵R

rij——各交通小区之间相似系数，得到模糊相似矩阵为：

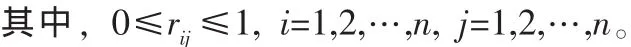
STEP4：模糊等价矩阵

由标定所得到的矩阵R一般为相似矩阵，不满足传递性，故本文采用平方自合成法，将R转换为模糊等价矩阵Rt。具体做法为建立相似性关系R的传递闭包，做成合成运算。

当存在一个数k，使得R2k=Rk·Rk时，停止计算。令Rt=Rk。

STEP5：模糊聚类

设定不同的置信水平λ∈［0,1 ］，对模糊等价矩阵Rt进行聚类处理。若Rt中的元素Cij≥λ，则将集合X中的ui和uj归为一类，从而得到一系列分类结果。

5 实例分析

现以某市一个行政区为例。初步方案将该区分为8个交通小区。各交通小区的指标值见表1。

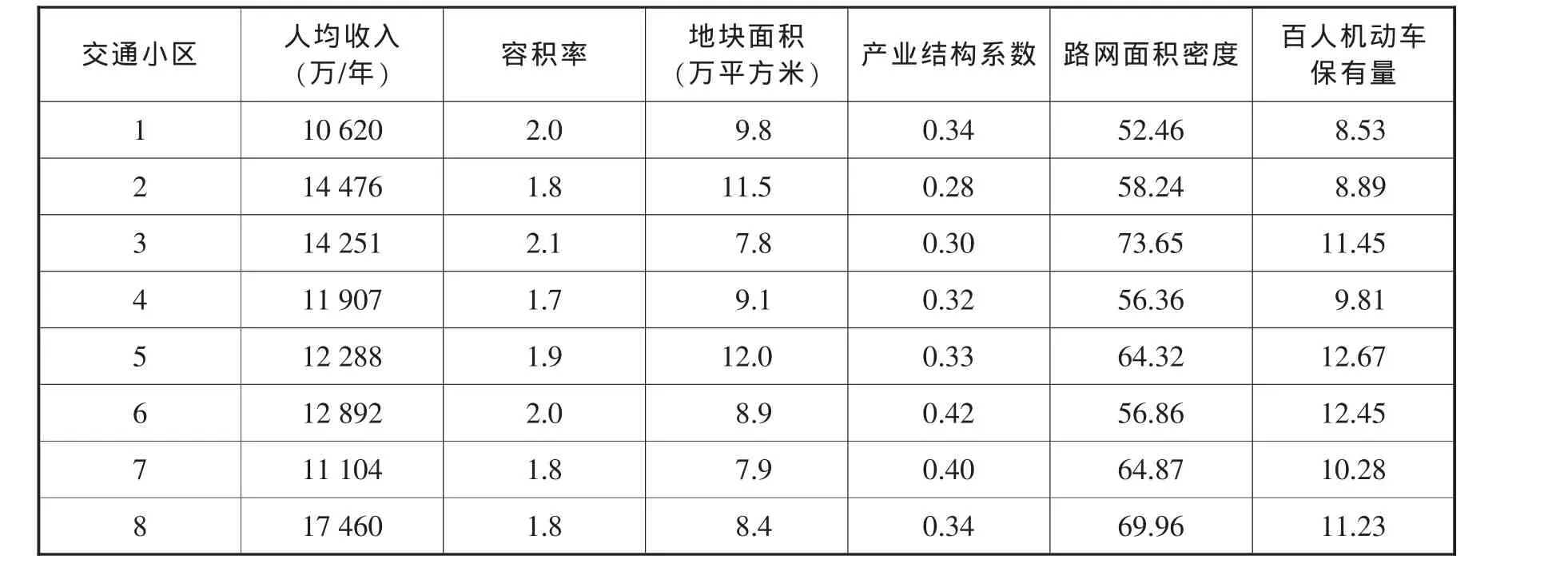
表1

运用MATLAB软件求得模糊等价矩阵，如表2所示。

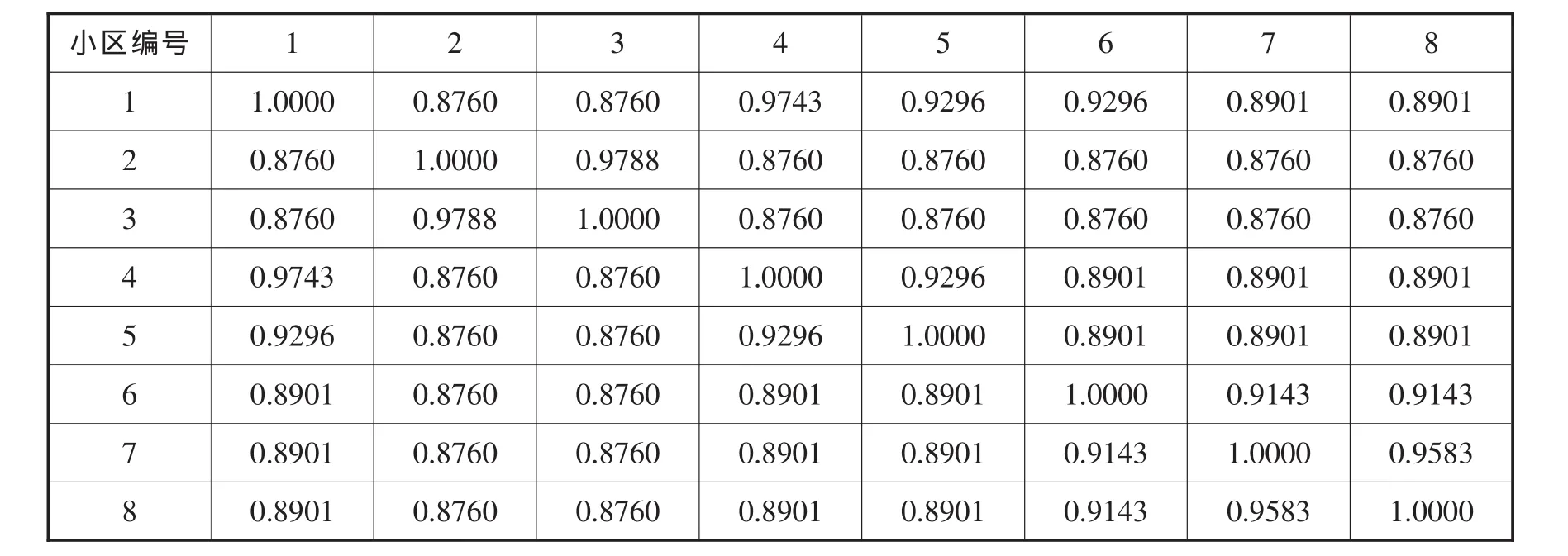
表2

不同置信水平λ，得到分类效果如表3。

表3

确定最佳阈值λ，取∂=0.005，每种分类对应的F统计量如表4。

表4

由表4可知， 当 λ=0.8901和 λ=0.9143时，Fr>F0.05（r-1,n-r）。 且F2-F0.05（1,6）=1.07，F3-F0.05（2,5 ）=1.60。 最佳阈值为 λ=0.9143。 把原样本分为3类。 ｛1,4,5｝,｛2,3｝,｛6,7,8 ｝。

6 总 结

交通小区划分是进行解析复杂城市交通网络的有力工具。运用模糊聚类方法对交通小区进行重新分类，为进一步规划工作提供了前提条件。

[1]高新坡.模糊聚类分析及作用[M].西安：西安电子科技大学出版社，2004.

[2]谢季坚，刘承平.模糊的数学方法的应用[M].武汉：华中科技大学出版社，2005.

[3]王瑞.城市居民出行调查若干问题研究[D].西安：长安大学 （硕士学位论文），2006.

Traffic District Division Method and Application Based on Fuzzy Cluster Analysis

LIU Yi-fei(Shanghai Maritime University Economics and Management School,Shanghai 200135,China)

This paper describes the definition of traffic zones,by the purpose and principles of traffic zone,based on fuzzy cluster analysis,using MATLAB software for clustering analysis,integration solutions.

traffic zones;fuzzy cluster analysis;MATLAB

F570

A

1002-3100(2011)09-0025-04

2011-06-01

上海海事大学研究生创新项目，项目编号：yc2010015。

刘乙霏（1988-），女（壮族），山东临沂人，上海海事大学经济管理学院硕士研究生，研究方向：交通运输规划与管理。