九架棚大桥0号块浇筑水化热温度场分析★
袁林婷 周太全 华 渊
1 概述
九架棚大桥为66 m+120 m+66 m的预应力混凝土连续刚构桥,采用悬臂挂篮现浇法进行施工,主墩处箱梁0号块节段浇筑块较大,长度达到12 m,底部宽度为5 m,底板厚度为1 m,顶板厚度为34 cm,梗腋处厚度为80 cm。
2 温度场热传导控制方程
混凝土温度场的计算其实质是热传导方程在特定边界条件和初始条件的求解。热传导方程为[1]:
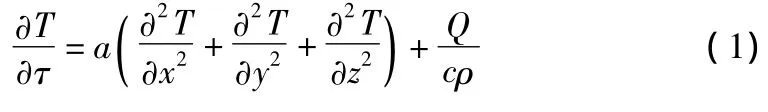
其中,T为温度;Q为物体内部的热源密度;a为导温系数;c为比热;ρ为密度。
由于水化热作用,在绝热条件下混凝土的温度上升速度为:

其中,θ为混凝土的绝热温升;W为水泥用量;q为单位重量水泥在单位时间内放出的水化热。
热传导方程可以改写为:

要求得热传导方程确定的解,必须知道方程的初始条件和边界条件。
初始条件为在初始瞬时物体内部的温度分布规律,有如下两种情况:
1)S=0时,温度场是坐标的已知函数。
2)S=0时,初始的温度分布是常数。
边界条件为混凝土表面与周围介质(如空气或水)之间温度相互作用的规律。通常有如下四类边界条件:
1)第一类边界条件:混凝土表面温度T是时间的已知函数。
2)第二类边界条件:混凝土表面的热流量是时间的已知函数。
3)第三类边界条件:当混凝土与空气接触时,经过混凝土表面的热流量与混凝土表面温度T和气温Ta之差成正比。第三类边界条件表示了固体与流体(如空气)接触时的传热条件。
4)第四类边界条件:当两种不同的固体接触时,如果接触良好,则在接触面上温度和热流量都是连续的。
根据初始条件和边界条件求解热传导方程,即可求得大体积混凝土的温度场。
3 水化热温度场有限元分析
ANSYS热分析基于能量守恒的热平衡方程,用于计算一个系统的温度等热物理量的分布及变化情况,能够计算各节点温度,并导出其他的热物理量。ANSYS热分析分为稳态热分析和瞬态热分析,前者系统的温度场不随时间变化,而后者系统的温度场随着时间发生明显变化。本工程箱梁0号段水化热温度场计算分析属于瞬态热分析。
3.1 0号块浇筑有限元建模
混凝土箱梁水化热温度场实质上是一个三维非稳态温度场问题。采用三维有限元实体模型进行模拟计算比较符合实际。采用ANSYS前处理建立梁体0号块的实体模型。0号块截面尺寸如图1所示。

图1 梁体0号块正立面

图2 梁体0号块有限元模型
利用0号块箱梁结构的对称性,建立实体模型时只取其1/4部分并采用实体单元Solid70对其模型进行实体剖分,实体剖分完成后共生成单元27059个,节点6061个,剖分完成后有限元模型如图2所示。
3.2 边界条件及计算参数的选取
根据施工时的自然条件及0号箱梁的结构形式设立箱梁边界条件。即0号箱梁与空气接触的外表面设为第三类边界条件。对模型边界施加水化热边界条件,本文水化热采取的模型为:朱伯芳[1]提出采用复合指数式表示水泥水化热和混凝土绝热温升:

设定计算时间为6×40=240 h,循环建立每小时生热量数组。定义牛顿—拉夫逊求解,初始混凝土入模温度设定为28℃,打开时间积分效果进行瞬态分析,荷载子步长定义为6 h。整个从建模、单元划分到荷载施加、求解过程采用APDL参数化语言[2]建立命令流文件,便于模型、参数的修改和调试。采用ANSYS瞬态热分析对0号块混凝土箱梁水化热温度场进行了有限元分析,分析结果如图3,图4所示。

图3 箱梁0号段温度场分布图
从图3分析结果中可以看出:在混凝土浇筑过程中,混凝土箱梁0号段的温度场最大值位于0号段中横隔板中心和顶、底板相交位置处,该处的混凝土厚度较厚,混凝土水化热较大,故会出现这种情况。
从图4可以看出:混凝土箱梁0号段在浇筑过程中,温度场经历了上升阶段和下降阶段,各个测点位置处的最大温度值发生在第2天,表明混凝土的水化热在浇筑后2 d内释放完毕,后面进入对流传热,温度逐渐下降直至箱梁内外实际温度。

图4 混凝土箱梁0号段温度场时程曲线
4 结语
九架棚大桥位于高海拔地区,0号块混凝土浇筑量大,昼夜温差较大。为对九架棚大桥0号块浇筑养护方案作出评价,采用大型有限元程序ANSYS进行了0号块水化热温度场分析。分析结果表明:0号块浇筑引起的最大水化热温度值发生在浇筑后第2天,温度和最大值位置位于0号段中横隔板中心和顶、底板相交位置处。
[1]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.
[2]商跃进.有限元原理与ANSYS应用指南[M].北京:清华大学出版社,2005.

