伺服系统中滑模变结构控制器的设计

谢远党，李维嘉，王春涛

（1.浙江海洋学院机电工程学院，浙江舟山 316004；2.华中科技大学轮机工程系，湖北武汉 430074）

线性系统在现代控制理论与应用中占有非常重要的位置，其基本理论已发展得相当完善，但是大多数实际系统是非线性的，建模时往往忽略了各种非线性因素影响才简化为理想的线性模型[1]。滑模变结构控制具有完全的自适应性，这是变结构系统最突出的优点。它不需要知道系统的精确数学模型，只需了解系统的参数及外来扰动变化的大致范围，并且具有降阶、解耦的功能，能较好地解决系统的动态、静态特性之间的矛盾，控制规律简单，它可以解决复杂系统，包括线性和非线性系统的镇定和品质等问题[2]。滑模变结构控制的设计在高精确度伺服系统的应用中受到日益广泛的重视。图1给出了本文所要讨论的滑模控制系统结构，它主要由受到控制器、PWM装置、直流无刷电机、机械试行机构、位置反馈单元组成。

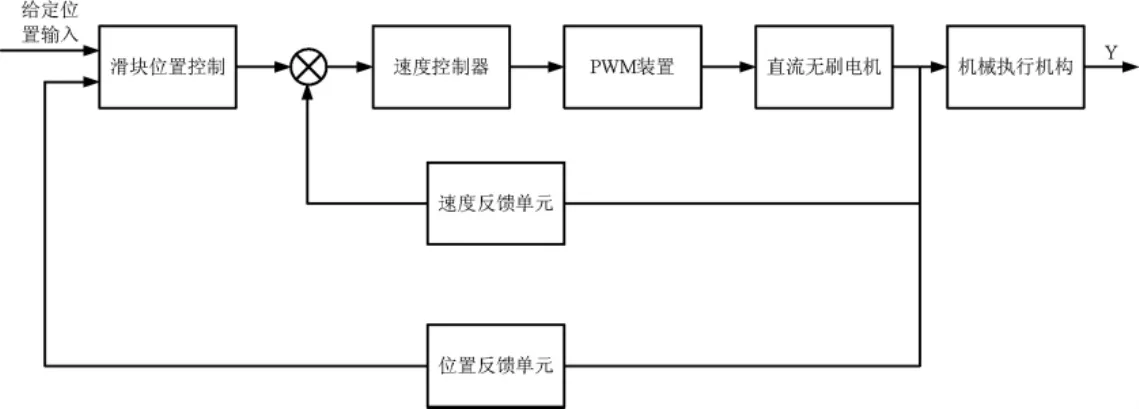
图1 无刷电机位置控制结构图Fig.1 No brush position chart of electrical control

1 滑模变结构控制概念

变结构控制（variable structure control,VSC）本质上是一类特殊的非线性控制，其非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的“结构”并不固定，而是可以在动态过程中，根据系统当前的状态有目的地不断变化，迫使系统按照预定“滑动模态”的状态轨迹运动，所以有常称变结构控制为滑动模态控制（sliding mode control,SMC），即滑模变结构控制。由于滑动模态可以进行设计且与对象参数及扰动无关，这就使得变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。

变结构控制出现于20世纪50年代，经历了50余年的发展，已形成了一个相对独立的研究分支，成为控制系统的一种设计方法，适用于线性与非线性、连续与离散系统、确定性与不确定性系统、集中参数与分布参数系统、集中控制与分散控制等[3]。并且在实际工程中逐渐得到推广应用，如电机与电力系统控制、机器人控制、飞机控制、卫星姿态控制等。这种控制方法通过控制量的切换使系统状态沿着滑模面滑动，使系统在受到参数摄动和外干扰时具有不变性，正是这种特性使得变结构控制方法受到各国学者的重视[4]。

2 滑模变结构控制基本原理

滑模变结构控制是变结构控制系统的一种控制策略。这种控制策略与常规控制的根本区别在于控制的不连续性，即一种使系统“结构”随时间变化的开关特性。该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动，即所谓的“滑动模态”或“滑模”运动。这种滑动模态是可以设计的，且与系统的参数及扰动无关。这样，处于滑模运动的系统就具有很好的鲁棒性[5]。

滑动模态控制的概念和特性如下：

（1）滑动模态定义及数学表达考虑一般的情况，在系统

它将状态空间分成上下2个部分s＞0或s＜0。在切换面上的运动点有三种情况，如

通常点——系统运动点运动到切换面S=0附近时，穿越此点而过（点A）;

起始点——系统运动点运动到切换面S=0附近时，从切换面的两边离开该点（点B）；

终止点——系统运动点到达切换面S=0附近，从切换面的两边趋向于该点（点C）；

在滑模变结构中，通常点与起始点无多大意义，而终止点却有特殊的含义，因为如果在切换面上某一区域内所有的运动点都是终止点，则一旦运动点趋近于该区域，就会被“吸引”到该区域内运动。此时，称在切换面S=0上的所有运动点都是终止点的区域为“滑模模态”区，或简称为“滑模”区。系统在滑模区中的运动就叫做“滑模运动”。

按照滑动模态区上的运动点都必须是终止点这一要求，当运动点到达切换面s(x)=0附近时，必有：

此不等式对系统提出了一个形如

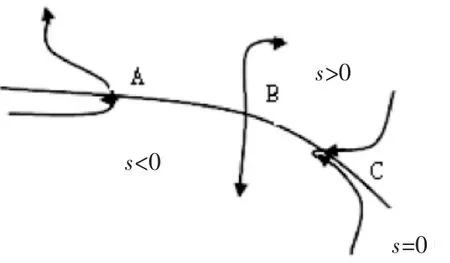
图2 切换面上3种点的特性Fig.2 Switch on the nature of the three

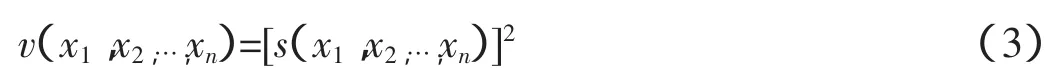
的李雅普诺夫（Lyapunon）函数的必要条件。由于在切换面领域内上面函数式是正式的，若按照的导数是负半定，也就是说在s=0附近v是一个非增函数。因此，如果满足条件式是系统的一个条件李雅普诺夫函数。系统本身也就是稳定于条件 s=0。

（2）滑模变结构控制的定义滑模变结构控制的基本问题如下：

设有一控制系统

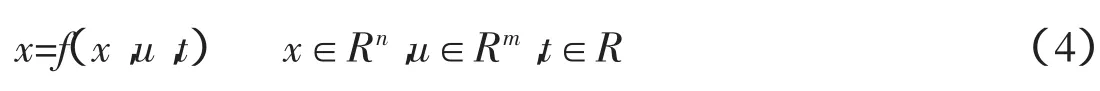
需要确定切换函数

s(x)， s∈Rm

求解控制函数其中，u+(x)≠u-(x)，使得

①滑动模态存在，则上式的控制函数存在。

②满足可达性条件，在切换面s=0以外的运动点都将于有限的时间内到达切换面；

③保证滑模运动的稳定性；

④达到控制系统的动态品质要求。

上述的前3点是滑模变结构控制的3个基本问题，只有满足了这3个条件的控制才可称为滑模变结构控制。

3 基于趋近率的滑模控制设计

滑模运动包括趋近运动和滑模运动两个过程。系统从任意初始状态趋向切换面，直到到达切换面的运动称为趋近运动，即趋近运动为s→0的过程。根据滑模变结构原理，滑模可达性条件仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求，而对于趋近运动的具体轨迹未作任何限制，采用趋近律[5]的方法可以改善趋近运动的动态品质。

3.1 几种典型的趋近律

（1）等速趋近律

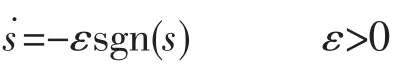
其中，常数ε表示系统的运动点趋近切换面s=0的速率。ε小，趋近速度慢；ε大，则运动点到达切换面时将具有较大的速度，引起的抖振也比较大。

（2）指数趋近律

指数趋近中，趋近速度从一较大值逐步减小到零，不仅缩短了趋近时间，而且使运动点到达切换面时的速度很小。对单纯的指数趋近，运动点逼近切换面时一个渐近的过程，不能保证有限时间到达，切换面上也就不存在滑动模态了，所以要增加一个等速趋近项，使当s接近0时，趋近速度是ε而不是0，可以保证有限时间到达。

在指数趋近律中，为了保证快速的同时削弱抖振，应在增大k的同时减少ε。

（3）幂次趋近律

（4）一般趋近律

其中 f(0)=0，当 s≠0，sf(s)＞0

显然，上述4种趋近律都满足滑模到达条件ss˙＜0。

3.2 基于指数趋近律的滑模位置控制器设计

变结构系统设计问题，主要是两个：第一个问题是如何正确地选择切换函数；第二个问题是如何求取变结构控制[6]。

我们所要设计的变结构控制是一个标量（单输入）控制，其切换函数具有如下形式：

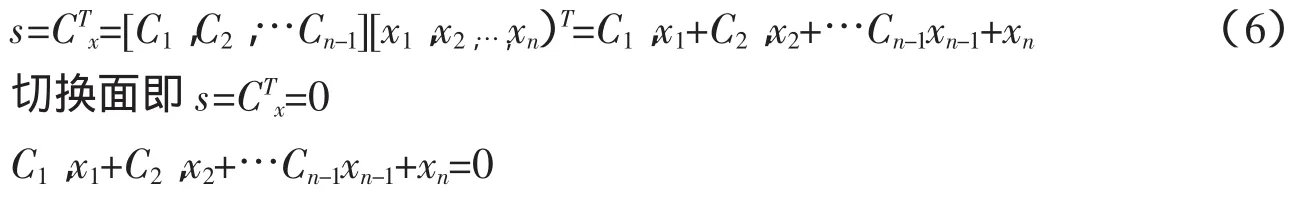
切换面的选择直接决定滑动模态稳定性与品质。选择切换函数就是如何求C矩阵的问题。一般来说，选择切换函数的常用方法有3种：

①极点配置法；

②二次型最优法；

③特征向量任置法；

3.3 系统滑模控制器切换函数（极点配置法）的设计步骤

本文选择极点配置法作为切换函数，其步骤如下：

其中x∈Rn，x∈Rm分别是系统的状态变量和控制变量[7]：

第一步：对上述线性系统作非奇异线性变换x=Mz，则可将其化为下列简约型：

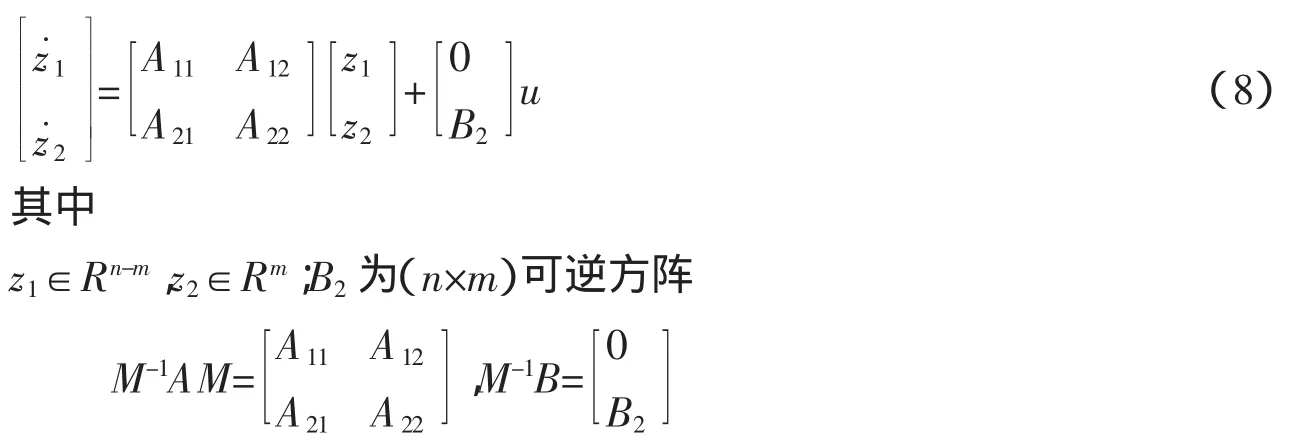
第二步：在此变换下，相应的切换面变为

其中，为可逆方阵。因此，在切换面上有

从而滑动模运动满足上式和下列降阶方程：

于是线性系统的滑动模可视为是由式（11）描述且具有反馈（10）的n-m维子系统，从而可以根据通常的线性反馈设计方法（如极点配置方法等）确定反馈系数矩阵F。

第三步：在原坐标系中按 s（x）=（F，Im）确定切换函数 s（x）。

由于系统在滑动时z2可以由z1线性表出，因此只要z1以适当的指数衰减趋近于零，则也以同样的指数衰减律趋向于零。取z2=Im，C1=F进而由式（9）和（10）可得到使原线性系统的滑动模一定具有良好动态特性的切换系数矩阵

C=（F，Im）M-1，从而得出切换函数 s（x）。

4 结论

在现代控制理论与应用中存在着非线性和不确定因素，而滑模变结构控制恰恰是解决这些问题的一种可行途径。本文主要介绍了滑模变结构控制器的原理，详细介绍了几种趋近率的计算方法，为了便于计算机控制，建立了基于趋近率的滑模位置伺服控制器的设计方案，它算法简单、易于实现，同时也能够满足系统跟踪精度的要求。

[1]姜 静,伍清河.滑模变结构控制在跟踪伺服系统中的应用[J].电机与控制学报,2005,9(6):1-4.

[2]易继锴,江祥贤,候媛彬,等.电气传动自动控制原理与设计[M].北京:北京工业大学出版社,1997.

[3]SABANOVIC A,IZOSOMOV D.Applicatioon of sliding modes to inductioon motor control[J].IEEE Transactions on Industry Applications,1981(IA-17):41-49.

[4]YOUNG K K D.Controller Design for manipulator Using Theory of Variable Structrue Systems[Z].IEEE Transaction on Systems,Man,and Cybernetics,SMC-8,1978:101-109.

[5]高为炳.变结构控制理论与设计方法[M].北京:科学出版社,1996.

[6]姚琼荟,黄继起,吴汉松.变结构控制系统[M].重庆:重庆大学出版社,1997.

[7]胡跃明.变结构控制理论与应用[M].北京:科学出版社,2003.