汽车动力转向油罐盖滚边力计算及试验研究

谈文鑫，廖义德，郭 敏，陈 方，邹军军

(武汉工程大学 机电工程学院，湖北 武汉 430074)

0 引 言

汽车动力转向油罐盖加工的工序很多，其安装密封圈的槽的加工就是其中的一步.汽车动力转向油罐盖安装密封圈的槽的加工一般采用冷滚压的方法.整个加工过程是汽车动力转向油罐盖发生弹塑性变形的过程，而所加工出的槽是油罐盖发生塑性变形的结果.目前，在生产实际中, 有很多要用到冷滚压工艺方法制造的零件，然而对于其滚压力的求解，还没有成熟的公式进行计算[1]，大多采用经验法和实验法.这两种方法都存在一些缺陷：经验法所求得的力只是参考值[2]，非常不准确；实验法周期很长，成本很高.这给油罐盖滚边机床的设计带来诸多不便.本文根据汽车动力转向油罐盖的受力变形特点，从静力平衡出发[3]，对其分部分进行分析，建立其加工过程中的滚压力理论计算的简化数学模型，并用相应的滚压实验进行验证.

1 滚压变形的特点

图1为加工前后汽车动力转向油罐盖的剖面图.油罐盖安装密封圈槽的加工过程：如图2所示，滚压轮向右进给，压在油罐盖CD段曲面上(见图1)，向油罐盖施加一个力F，油罐盖以n的速度逆时针旋转，带动滚压轮向相反的方向转动.当压力F较小时，板料产生弹性变形，随着F增大达到某一极限值时，油罐盖CD段及其附近开始发生塑性变形.当把力撤去时，这部分变形不会恢复，从而形成所要加工的槽.在加载的过程中，板料的变形过程是：弹性、弹塑性、塑性流动的过程[4].这里的塑性变形过程很复杂，如图1所示在滚压过程中，CD段发生的是先切向压缩后切向拉升的变形过程，EQ段主要是由CD下面附近圆弧段沿着一定的角度拉伸而产生的.ABC段主要是一个拉伸变形的过程，拉伸变形主要集中在C的附近，所以在C处很容易出现破裂现象.在整个加工过程中，板料在厚度方向变形非常小，所以在厚度方向的应力可以忽略为零[5].

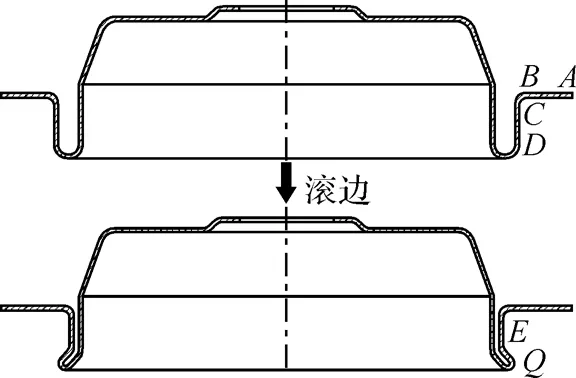
图1 加工前后油罐盖的剖面图

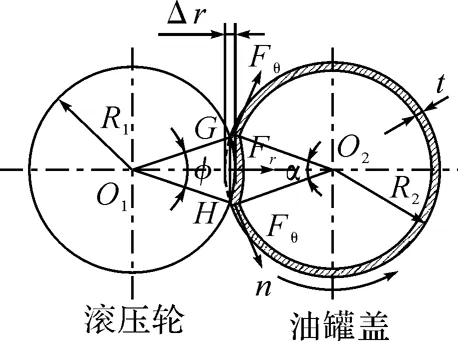
图2 受压曲面受力分析

2 滚压力数学模型的建立

假设汽车动力转向油罐盖每转一圈后，所加工出的槽的深度处处相等，即油罐盖每转一圈后，滚压轮进给一个深度.则在油罐盖每转一圈的过程中，滚压轮进给刚刚结束时候滚压力最大，这个力也是在油罐盖滚边机床设计时必须确定的力.根据前面分析的汽车动力转向油罐盖塑性变形的特点，在滚压轮进给刚结束的瞬间，先把油罐盖分为三部分分别进行受力分析，然后再把这三部分当作一个整体进行受力分析.

2.1 受压曲面变形力的计算

只对受压曲面进行受力分析，即对汽车动力转向油罐盖与滚压轮的接触面进行受力分析，不考虑CD段(见图1)上下两端应力应变的影响.如图2所示，把受力曲面看作以整体作受力分析，受压曲面边缘对受压曲面有支撑作用，支撑力主要是由变形而引起的，所以曲面的两边缘受到力Fθ作用，Fr为引起切向变形的力，滚压轮与油罐盖接触的接触面所对应的圆心角为φ，相应的弧长为L，油罐盖滚与滚压轮接触的接触面所对应的圆心角为α.

此时的力Fθ是由受压曲面边缘附近沿汽车动力转向油罐盖切线方向拉应变而产生的，所以Fθ的方向沿切向方向(如图2所示)，其大小为

Fθ=σθBt

(1)

式(1)中：σθ为受压曲面边缘附近切向应力，MPa；B为所加工槽的宽(滚压轮的宽度与槽宽相等)，mm；t为为汽车动力转向油罐盖所使用板料的厚度，mm.

沿径向列出受力曲面的平衡方程：

(2)

将式(1)代入式(2)，整理得

(3)

受压曲面两边缘附近主要发生的是塑性变形，忽略加工硬化效应，则可取σθ=σs，σs材料的屈服强度，将σθ=σs代入式(3)得

(4)

2.2 槽壁变形力的计算

前面已经分析过槽壁EQ(如图1所示)是由CD下面附近圆弧段沿着一定的角度拉伸的过程.取EQ段上非常靠近受压曲面的部分进行受力分析，其上作用有引起拉伸变形的拉应力σ1，如图3所示，EQ段与水平方向的夹角为β.

EQ段上非常靠近受压曲面的部分对受压曲面产生拉力作用[6]，其大小为

F1=σ1Lt

(5)

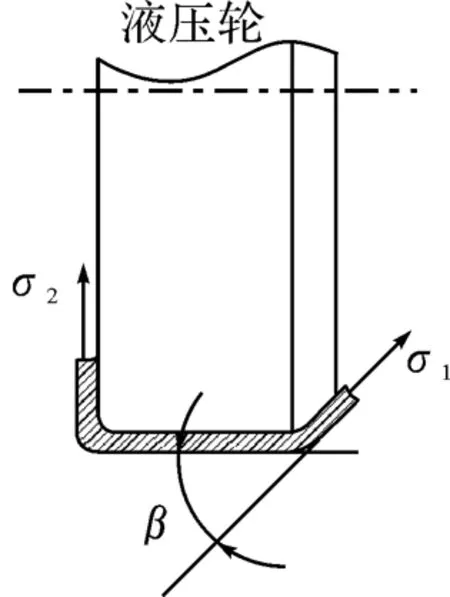
图3 槽壁受力分析

在加工过程中，油罐盖转速n通常都很大.槽加工完成时，油罐盖往往已经转过了几十到几百圈，而所加工槽的深度一般为几个毫米，所以油罐盖每转一圈，滚压轮压入的深度非常小，即受压曲面所对应圆心角很小.如图2所示，∠GO1H与∠GO2H很小，所以可以取L=GH，经过推导得：

(6)

式(6)中:Δr为滚压轮压入油罐盖的深度，mm；R1为滚压轮的半径，mm；R2为油罐盖加工面的半径，mm.

在EQ段上非常靠近受压曲面的部分主要发生的是塑性变形，忽略加工硬化效应，则可以取σ1=σs.将式(6)，σ1=σs代入式(5)，整理得：

(7)

油罐盖上的盘形结构，即图1所示ABC段，在加工过程中发生变形形成槽壁(靠ABC段这边的槽壁).如图3所示，取槽壁非常靠近受压曲面的部分进行受力分析，其上作用有引起拉伸变形的拉应力σ2，从而对受压曲面产生拉力作用.其大小为

F2=σ2Lt

(8)

同槽壁EQ段一样，取σ2=σs.将式(6)，σ2=σs代入式(8)，整理得：

(9)

2.3 滚压力的计算

把三部分当作一个整体进行受力分析如图4所示.沿y轴方向列出受力曲面的平衡方程：

Fr+F1sinβ+F2-F=0

(10)

式(10)中：F为滚压轮施加在油罐盖上的压力，N.

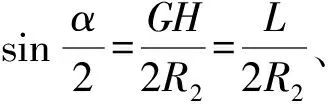
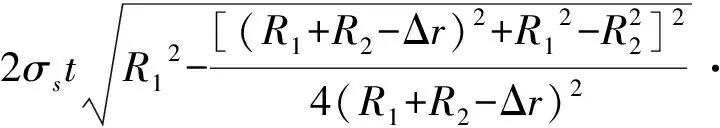
(11)

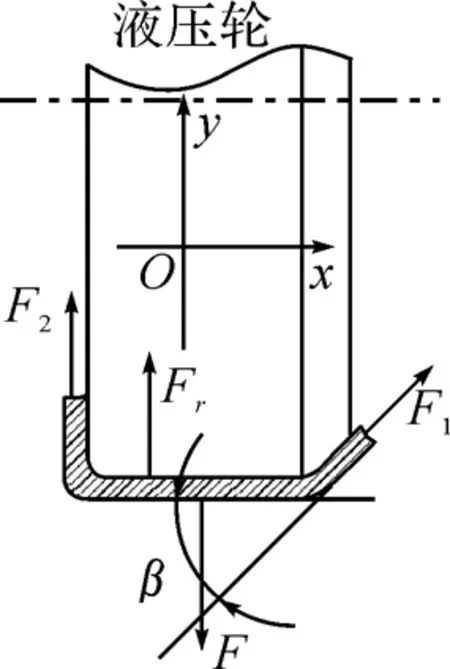
图4 整体受力分析

3 实 验

3.1 实验目的及设备

为了验证该滚压变形力理论计算新模型的正确性,在此进行滚压工艺和模拟试验.为了使试验结果更接近真实值，专门设计了一台汽车动力转向油罐盖滚边的实验设备.实验设备主要由电机、送料机构、导料机构、传动机构、进给滚压机构、定位夹紧机构等部分组成，如图5所示.

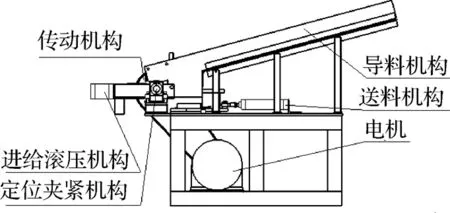
图5 滚压力测试实验设备

3.2 实验内容

工艺试验的材料为厚度t=1.2 mm的碳素钢Q195，即该材料的屈服强度σs=195 MPa，滚压轮的半径R1=48.75 mm，所加工槽的槽宽B=12 mm，角β=30°.主要要使用3140油罐盖、3408油罐盖、602油罐盖三种型号汽车动力转向油罐盖进行试验.其加工面的半径R2分别为73 mm、60 mm、50.75 mm.试验表明当压入深度Δr约为0.05 mm时，三种型号的油罐盖都开始发生塑性变形.在实验中，测出刀具进给时进给油缸进油口压力和出油口压力，然后用公式(12)计算出滚压力，得到实验值.

F=P1A1-P2A2

(12)

式(12)中:F为滚压力，N；P1为进给油缸进油口压力，MPa；P2为进给油缸出油口压力，MPa；A1为进油腔活塞有效作用面积，mm2；A2为出油腔活塞有效作用面积，mm2.

将三种油罐盖刚开始发生塑性变形时加载力理论计算值与实验值如表1所示.

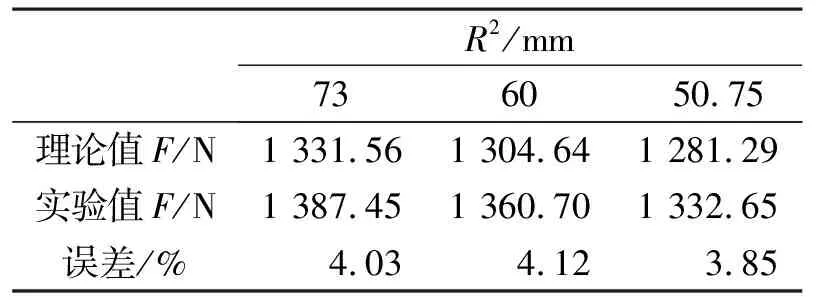
表1 刚发生塑性变形时理论值与试验值对比

随着压入深度Δr增大，滚压轮与油罐盖的接触面也随之增大，所以滚压力F会随着压入深度Δr增大而增大.对3140这种型号的油罐盖做不同压入深度时加载力的验证试验，将不同压入深度时加载力的计算值与实验值如表2所示.

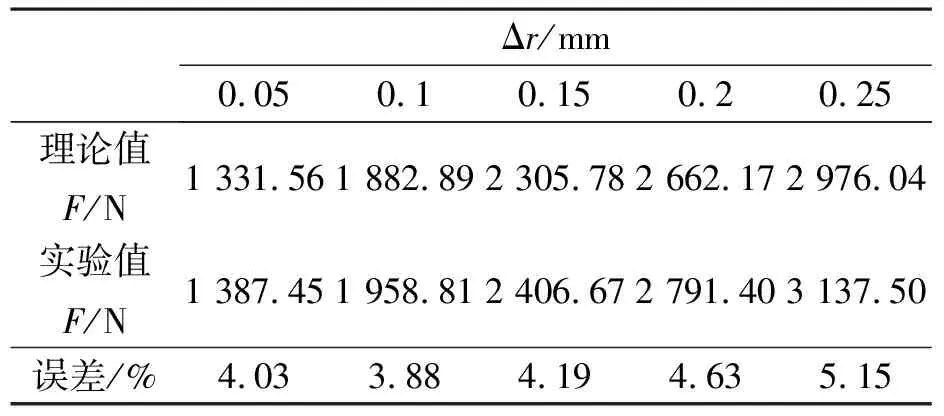
表2 不同压入深度下理论值与试验值对比

3.3 结果分析

通过表1、2中的数据，会发现理论值普遍比实验值小，而且表2中的误差值(除压入深度为0.05 mm外，此时汽车动力转向油罐盖刚发生塑性变形)随着压入深度增大逐渐增大的趋势.造成这一现象的原因主要有：①计算时忽略加工硬化效应的影响[7]；②计算弧长L使用的公式不精确，压入深度Δr越大，产生误差随之增大.但误差都在6%以内，在允许的范围内.

4 结 语

a.针对汽车动力转向油罐盖安装密封圈的槽的冷滚压加工滚压力的计算，目前常采用的方法存在着求解不准确，周期很长，成本很高等问题，提出了一种简化计算方法.为此类机床设计时滚压力的确定提供一些理论参考.

b.通过理论计算与实验结果对比，虽然理论值普遍比实验值小，但误差都在6%以内，在允许的范围内，这表明新建的模型与滚压变形的实际基本相符.但压入深度很大时，不宜用公式(6)求弧长.

参考文献：

[1] 郭长江,杨改云,赵利德.滚压成形力的数值计算与模拟[J]. 机床与液压,2007,35(10):101-102.

[2] 顾青丽. 风电螺栓螺纹滚压工艺参数的选择[J].电气制造,2010(10):62-64.

[3] 张守茁,席镇,孙海花,等.圆筒形件拉深过程的力学理论分析与计算[J].内蒙古工业大学学报:自然科学版,2006,25(3):183-189.

[4] 关桂芳,刘志坚,郭金基,等. 计算冷挤压成型钢盔挤压力的滑移线法[J].暨南大学学报:自然科学版,1999,20(1):34-37.

[5] 卢险峰,谭欣珍,周勇,等.拉深变形力理论计算模型研究[J].中国机械工程, 2008,19(16):2004-2006.

[6] 李尧.金属塑性成形原理[M].北京: 机械工业出版社,2004.

[7] 卢险峰,周勇,盛自强.考虑冷变形加工硬化的翻边力理论计算[J].南昌大学学报:工科版,2009,31(2):187-191.