基于电流逆灌注法的经络可视化研究

王学民 罗 鸣 马晓雷 周 鹏 王忠海 马思宇

(天津大学精密仪器与光电子工程学院，天津 300072)

引言

经络是中医理论的基本概念之一，是指人体机能活动联络、调节和反应的体系。经络作为中医的最重要的内容和基础之一，研究其实质、用现代科学的方法去揭示其存在的形式和规律，是中医与现代科学接轨的重要途径［1］。虽然国内外已有很多学者在研究经络的实质，但是还没有确凿、完善的实验和理论能够证明和说明经络。经络的实质是什么?这一问题一直困扰医学界，也是生命科学和医学界迫切需要解决的重要学术问题。因此，需要借助现代科学技术，从各个方面不断地研究经络的现象和特性，将中西医更好地结合起来，从而更深入地研究经络的本质。

随着经络研究的不断深入，研究者从各个角度对经络进行了研究，使人们对经络的一些特殊现象有了更进深入的认识，如经络的低流阻通道特性、经络的循经感传现象、经络的电阻抗特性等［2－4］。其中，经络的低流阻通道特性可以表述为:经络的组织间质在沿经络的方向上，流导较大或流阻较小;在靠近经络的方向上，流导越来越大，流阻越来越小。此假设也可称为经络的低流阻假设。这些现象都是对经络这一客观事实的进一步确认，也为经络物理模型的建立奠定了理论基础。

本研究在经络的循经感传现象和经络的低流阻特性的理论基础上，首次提出了一种经络研究的新方法。采用Comsol软件，建立经络的简化三维物理模型，并用信息流注入的方法，研究信息流在经络和非经络上的传导特性。在此基础之上，采用动态成像原理及截断奇异值分解正规化算法，在一个横截面上进行边界电压值的测量，根据边界电压值的差值，重建经络模型的电导率分布，为经络的可视化研究提供了有利的科学依据。

1 经络模型建立

研究表明，人体各组织具有不同的电特性［5］，人体各组织的电导率如表1所示。根据经络的生物物理特性，经络作为一种具有低流阻特性的通道，可以运行组织液，也可以使组织中的化学物质通过这一通道进行运输和交换，一些物理量(如电流、电磁波、压力、热等)也可循着这条通道进行传播。可以假设经络对这些物理量的传输效果更明显，在电特性方面具有较高的电导率。

表1 人体各组织的电导率Tab.1 Conductivity of human tissues

因此，为了更方便地研究经络，本研究采用Comsol软件，建立了模拟人体臂部大肠经的简化物理模型，模型直径为10 cm、高为15 cm。如图1(a)所示，圆柱为人体臂部的简化模型，小圆柱体为经脉的低流阻通道，其余部分为肌肉组织，电导率值分别选择0.7和1。在图1(b)中，小圆柱顶部的电极为注入电流激励电极，底部的圆圈为围绕圆柱底部均匀分布的地电极，中间为8个测量电极。本研究采用动态成像的方法，分别从经络口和非经络口注入电流，根据两种方式的差值来研究经络的特性参数。

图1 人体臂部的简化模型。(a)人体臂部简化模型;(b)模型电极分布Fig.1 Simplified model of human arm.(a)simplified modelof human arm diagram;(b)electrode distribution model

正问题就是已知物场的分布和敏感场的初始及边界条件，求取电磁场分布。通常采有限元法进行求解，本研究采用Comsol软件进行电磁场有限元仿真。图2为物理模型的剖分图，通过Comsol软件对所建模型进行了三维剖分，以便求出其灵敏度矩阵。图3为在经络口注入电流时的电压分布，可以很明显地看到在靠近所设经络区域，电导率明显比其他区域要高。

图2 物理模型的三维剖分Fig.2 Three-dimensional physical model of subdivision

图3 物理模型测量截面的电压分布Fig.3 Physicalmodel of the voltage distribution measured cross section

由于反问题的计算采用基于灵敏度定理的方法，因此需要构建灵敏度矩阵J，这也是正问题所需解决的一个重要问题。灵敏度矩阵是基于场域内电导率的微小变化，而引起边界测量电压变化的原理，实现非线性问题的线性化处理。因此，线性化物理模型可表示为

式中，J为线性化系统矩阵(灵敏度矩阵)，Δσ为在经络口和非经络口注入电流时对应的电导率变化，ΔU为电导率变化引起的边界电压变化。

对于已经建立的模型，为了减少问题的病态性，采用方形网格进行灵敏度矩阵求解以及逆问题计算。将成像区域分成一个个小区域，每一个区域电导率为常量，经过一系列的推导［6］，可以得到灵敏度矩阵的计算公式为

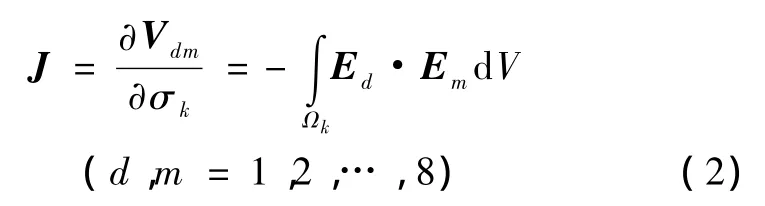
式中，Vdm为第d种和第m种类型的电流激励条件下的电势差，σk为第k个区域的特征表达式(电导率)，Ed和Em分别为第 d种和第m种类型的电流激励条件下的电场强度分布。

由式(2)获得了该模型的灵敏度矩阵，为经络模型反问题的求解奠定了基础。

2 TSVD正则化方法

根据边界电压的测量值，通过适当的算法，求得模型内的阻抗分布或阻抗变化，这在电磁场分析中被称为逆问题，而对经络特性参数的图像重建就是对反问题的求解。对于经络特性参数的重建，需要借助一定的先验知识，主要包括经络组织的结构特征以及一般组织的电导率分布信息。

通过计算得到灵敏度矩阵J，分析这个矩阵的相关参数，可知它的条件数为 cond(A)=1.48×1028很大，因此矩阵J是一个病态矩阵，求解式(1)是一个不适定问题。奇异值分解是分析不适定问题的一种非常有效的方法，而截断奇异值分解(TSVD)正则化方法已经成功解决了许多不适定问题，因此本研究采用截断奇异值分解的正则化方法。

根据所求的灵敏度矩阵，采用截断奇异值的正则化方法［7－10］，用一个良态的亏秩矩阵 B来近似A。所谓良态的亏秩矩阵，是指这个矩阵的条件数

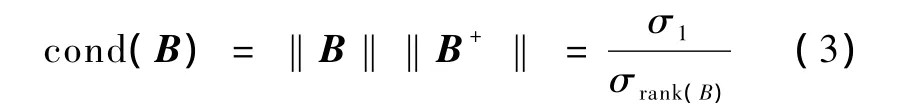
不是很大。

定义:设 A∈ Rm×n的奇异值分解由 A =给出，给定 ε ，取 k(ε)满足

即 σ1≥ … ≥ σk(ε)≥ σk(ε)+1≥ … ≥ σn，则

称为A的截断SVD分解(truncated singular value decomposition，TSVD)，k(ε)为截断参数。在不引起混淆的情况下，记Ak(ε)为Ak，实质上是通过控制ε滤掉对矩阵性质影响较大的小奇异值。当A是从有噪声的观测数据得到时，这种方法能够起到很好的作用。因此，可以将问题转化为求解

其最小二乘解为

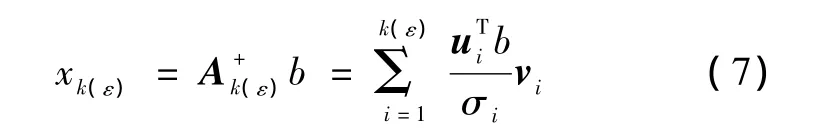
这就是TSVD正则化方法。

为了确定k(ε)，采用范数比的方法。

3 结果

为了更好地研究灵敏度矩阵的性质和算法的比较，先假设经络在圆形场域的中间，其电导率的分布如图4所示，中心部分的电导率高于周围部分的电导率。采用动态成像原理，分别从经络口和非经络口(靠近经络处)注入频率为100 Hz、有效值为10 mA的激励电流，通过截断奇异值分解正规化算法，重建模型电导率分布。

图4 模型电导率分布Fig.4 Conductivity distribution model

根据范数比的定义计算范数比，有

由于截断参数与噪声是相关的，在不同的参数下相关系数是不一样的，因此选择υ(k)≥α=0.999 9的最小整数 k=19作为截断参数，成像效果如图5所示。

图5 k=19时的图像重建结果Fig.5 The image reconstruction when k=19

然后，在计算得到的测量数据中分别加入1%和5%的随机噪声，成像效果如图6所示。图6(a)是在所测得的数据中加入1%随机噪声后重建所得，图6(b)是在所测得的数据中加入5%随机噪声后重建所得，两幅图的电导率分布基本没有变化，且圆心部位的电导率都明显比其他区域的电导率要高。可见，该截断参数能够起到较好的图像重建效果，使灵敏度矩阵J的条件数减小，起到抑制噪声的作用。

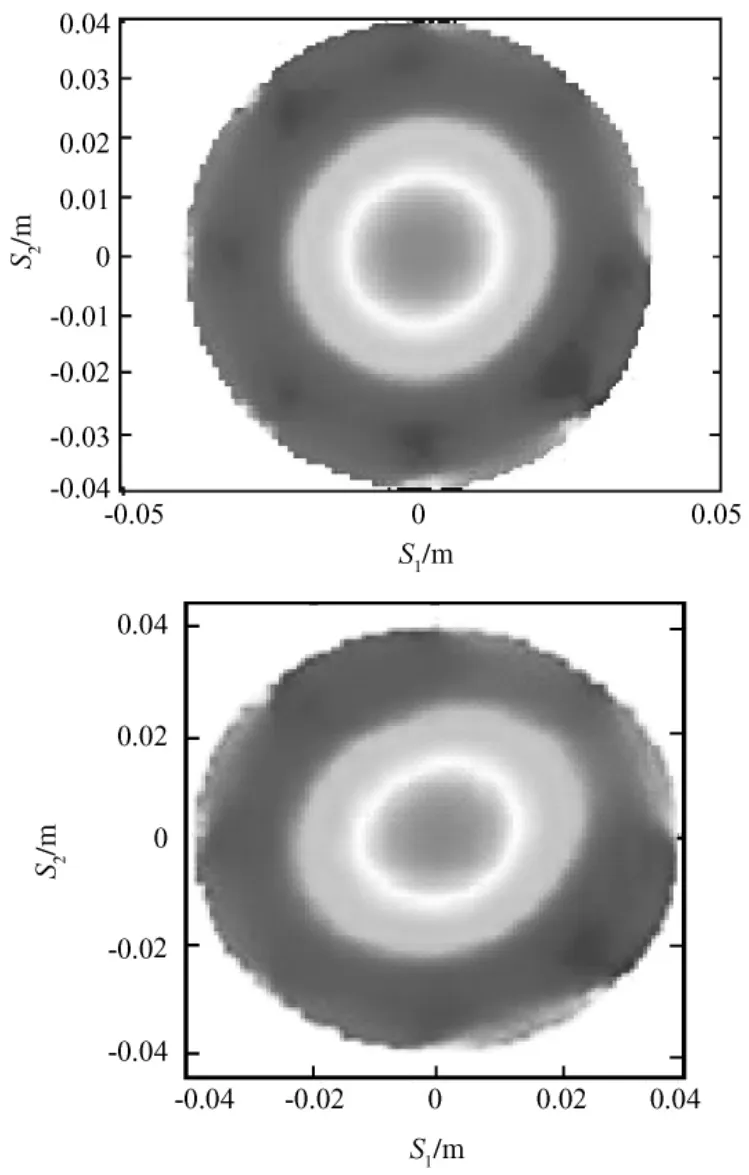
图6 加入不同水平噪声时的图像重建结果。(a)1%;(b)5%Fig.6 Image reconstruction by adding different random noises.(a)1%;(b)5%

对于经络特性的研究，引用一些先验知识(包括内部组织的结构特性和组织的电导率信息)，建立了三维的经络物理模型，图7为经络物理模型的原始电导率分布。采用电流激励-电压测量的方式，分别从经络口和非经络口注入电流，测量两种方式的电压值，通过差值研究经络的特性参数。根据动态成像的方法，采用截断奇异值分解算法，图像重建效果如图8所示，可以明显看到经络部分高于周围其他部分的趋势。

4 结论

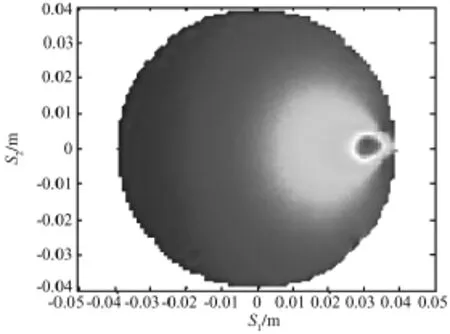
图7 经络物理模型原始电导率分布Fig.7 Physicalmodelofthe originalconductivity distribution Meridian

图8 重建经络模型电导率分布Fig.8 Meridian reconstructed conductivity distribution model

本研究在经络的低流阻特性和生物物理特性的基础上，合理地建立了人体臂部的简化数学模型。然后，提出了一种经络研究的新方法——纵向注入电流、在一个横截面上进行边界电压的测量。采用在经络口和非经络口注入电流的方法，研究电压分布情况的差异。采用有限元法和Comsol软件进行了电磁场的仿真，得出了灵敏度矩阵公式。最后，采用动态成像方法和截断奇异值分解的正则化算法，基于先验知识重建了经络模型的电特性分布(电导率)，为进一步研究经络的本质提供了新的方法。

［1］费伦，魏瑚.经络学说基础理论的构建及其学术地位的确立［J］.世界科学，2005，9:43－45.

［2］刘芳，黄光英.经络的生物物理学、化学特性的研究进展［J］.针刺研究，2007，32(4):281－285.

［3］杨威生.低阻经络研究Ⅲ 对经络组织学本质的推断［J］.北京大学学报(自然科学版)，2008，44(2):227－280.

［4］王永红.经络的实质探析［J］.世界中医药，2010，5(4):236－237.

［5］王研.EIT固定参考点图像重建和电极结构优化方法研究［D］.北京:中国协和医科大学，2002:1－5.

［6］Polydorides N，Lionheart WRB.A Matlab toolkit for threedimensional electrical impedance tomography:a contribution to the electricalimpedance and diffuse opticalreconstruction software project［J］.Measurement Science and Technology，2002，13:1871－1883.

［7］聂守平，魏晓燕.数字图像的奇异值分解［J］.南京师大学报，2001，24(1):59－61.

［8］黄小为，吴传生，朱华平，基于奇异值分解建立的一种新的正则化方法［J］.数学物理学报，2005，25A(3):331－336.

［9］黄小为，吴传生，李卓球.TSVD正则化方法的参数选取及数值计算［J］.华中师范大学学报，2006，40(2):154－157.

［10］董超峰，孙方裕.基本解方法求解各向异性材料中热传导方程的时间反向问题［J］.浙江大学学报，2007，34(1):33－39.