量化分析在医院人力资源管理决策中的应用

苗木 江苏省苏北人民医院

医院人力资源决策是关于医疗行为和相关的社会活动的医院人力资源主体的决策，是医院人力资源开发、利用和管理的重要依据，对医院管理的其他决策具有深远的影响。决策的科学与否直接关系到卫生人力资源管理目标的实现，关系到医院改革的成败。科学的决策需要科学的手段和理论为指导，需要有合理的程序进行论证，需要具有先进思维方式的决策者进行实施。为实现医院人力资源最优管理的目标，需运用科学的方法，特别是量化分析方法，做出若干可供选择的有关人力资源管理活动的行动方案，并在其中做出最佳选择，直至医院人力资源管理得以优化。

方法一

模糊决策理论在人员招聘决策中的应用 人员录用与招聘是人力资源管理重要职能，为医院招聘到优秀人才，从而为医院发展提供人才保证是十分重要的工作。但在招聘时常会遇到在众多医学人才中进行择优的问题，好与不好没有绝对的衡量标准，孰优孰劣难以判断，这是客观存在的现象即模糊现象。为了规避或降低人才招聘的风险，试运用以模糊数学为基础的模糊决策理论来解决人才招聘中的模糊现象问题。例如：医院欲从医学院校毕业的6名本科生中录用一名，经研究需要考虑5项评价要素：（1）在校期间学科成绩；（2）外语与计算机技能水平；（3）价值观和抱负（政治面貌、组织鉴定）；（4）第一印象（言谈举止、气质风度、反应速度）；(5)人际关系处理能力（团队精神、对压力的反应）。经过面试专家小组的面试和全面考察取得了6名医学毕业生的特征，见表1。

根据得出的特征差别，将V=｛差、中、良、优｝化分为［0 1］之间的指标行向量：

V=｛0；0.3；0.8；1｝，另外根据测试研究得到5项要素的权重分别为：

W=｛0.3；0.2；0.2；0.15；0.15｝，则上述图表可以转化为一模糊矩阵见图1。

图1 模糊矩阵

从上述计算结果可知第三项最大，因而录用C生是最佳选择。

注意事项 （1）评价要素确定的合理性；（2）评价要素权重比例划分的科学性，这两点关系到整个招聘决策准确性。

方法二

决策树在医院人力资源激励决策中的应用 激励决策是为了提高广大医护工作者的救死扶伤、为病人服务的工作积极性，应根据具体的医疗岗位采取适宜的激励手段。科学的激励措施会极大地激发医护人员工作热情，促使他们在工作中团结、努力。大多数激励措施都是从物质激励和精神激励这两个方面来进行的，那么，究竟在一次激励行为中采取哪种方式能达到最佳效果呢?下面引进决策树来举例分析。

决策树是以图解方式分别计算各个方案在不同情况下的损益值，通过比较做出选择，将可行方案、影响因素绘制成树形图。例如：医院为在5年内提高医护人员的工作积极性，从而促进医院效益的增长，决定从发放奖金、发放物品和出国培养三种方案中选择一种。三种方案的费用分别为340万元、270万元、400万元。

第一，通过调查得到表2数据。

第二，绘制决策树：按5年计算三种方案的综合收益值：

表1 6名大学毕业生的特征

发放奖金：[0.6×1000+0.25×800+0.15×100]×5=815（万元）

发放物品：[0.6×800+0.25×600+0.15×200]×5=660(万元)

出国培养：[0.6×1200+0.25×900+0.15×120]×5=963（万元）

发放奖金净收益：815-340=475

发放物品净收益：660-270=390

出国培养净收益：963-400=563

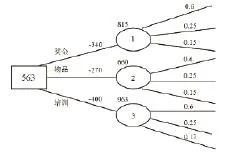
图2 决策树

第三，方案优选：比较三个方案计算结果，出国培养的预期收益为563万元，大于奖金发放和物品发放方案的收益，所以出国培养是最优方案。

注意事项 一是决策前必须进行深入细致的调查；二是概率分析的准确性关系到整个决策的准确性。应认识到运用决策树是有局限性的。

方法三

匈牙利法在医院人力资源开发决策中的应用 医院人力资源开发通常是通过对医技人员进行培训、进修、继续教育等形式，来提高业务素质，更新知识结构，掌握新技术，从而提高专业技术水平和开展新技术。此项工作在操作过程中会遇到这样的问题：医院往往希望用最短的时间完成数个待培人员的培训任务，使正常的医疗活动不受影响。

如：有四项医疗新技术要4位医务人员去学习，每人要求掌握其中一项，不同的人完成学习的时间不同（如表3所示），那么如何安排才能最快完成？在此我们引进匈牙利法解决该问题。

表2 调查结果分析

表3 医技人员进修时间表 （ 单位：天）

第一步，首先按上表列出矩阵[1]。

第二步，约简矩阵。在矩阵的每行中选出最小（值）元素，然后将该行的各元素减去此数，得到矩阵[2]。

第三步，继续约简矩阵。在行约简后的矩阵中没有“0”的列再约简，即从该列中选出最小元素，并将其他元素减去此数，得到矩阵[3]。

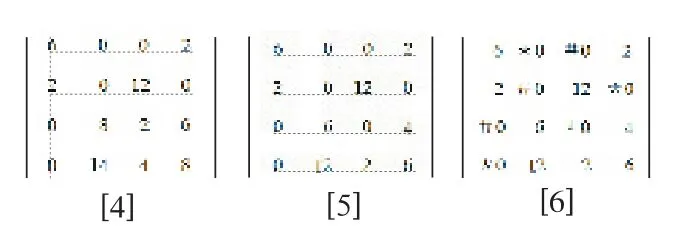
第四步，检验是否取得最优分配方案[4]。对[3]做过零覆盖线，即对有“0”的行或列划一条覆盖线，能覆盖所有零元素的最少覆盖线称维数，当维数等于矩阵的阶数时，就可得出最优分配方案，若维数少于阶数，还要进行调整。

第五步，进行调整。找出所有没有被覆盖元素中的最小元素，这里是“2”，将不在覆盖线交叉点上的元素减去“2”，其余元素不变，得矩阵[5]。

第六步，作覆盖线[5]，并检查是否取得最优方案。现在最小覆盖线的条数为四，与矩阵阶数相等，因而确定得到最优方案。

第七步，确定最优分配方案。按行（或列），对有一个零元素的行（列）先分配（记*号），分配后，划去与该零元素同列（或行）的其他零元素（记＃号）。得到分配方案为：

最优分配方案：丁（A）、丙（C）、甲（B）、乙（D）

时间总计为：16+22+10+12=60天

注意事项 （1）每项学习的时间必须有明确的规定；（2）对参加学习的医务人员的学习能力应充分了解。

上述对医院人力资源决策中的招聘、激励、开发等决策采用了量化分析的方法，事实上医院的人力资源决策还包括很多内容，不同的决策需要不同的分析方法，有待于实践工作中总结和研究。

1 刘桂卿，熊桂华.标准量化积分在护理综合评价中的应用[J].中华医院管理杂志，2001,17(4):235-236

2 彭剑峰，荆小娟.员工素质模型设计[M].北京：中国人民大学出版社，2003

3 王蕴，素质测评技术在人员招聘中的应用[J].商场现代化，2006(5)中旬刊：245-246

4 苗木，鞠永和.浅析城市大医院的功能定位与发展战略[J].医院管理论坛，2009,26(2)