不同虫态施用杀虫剂对下一代昆虫种群数量的影响

陶 杰，胡雅辉，贺淑岚

（湖南省植物保护研究所，湖南 长沙 410125）

确定杀虫剂的最佳施用时间是施药技术中重要的一个环节，对控制害虫有着重要的作用[1-6]。为了使杀虫剂的效果最大化，这不仅需要知道害虫种群的发生密度，也需要知道害虫发生的虫态，而大多数害虫往往具备卵、幼虫（或若虫）、蛹（或伪蛹）和成虫这几个虫态，在幼虫期又根据蜕皮的次数分为不同的龄期。昆虫对杀虫剂的敏感性不但取决于杀虫剂的种类，也取决于昆虫的种类和虫态[7]。长期以来，农民和研究者通常把昆虫对杀虫剂最敏感的发育时期作为最适施药期。但是，根据害虫综合治理的原则[8]，施用杀虫剂的主要目的是使下一代害虫种群的数量降到最低，而不只局限在使当代害虫种群的致死率最高。笔者提供的模型就是以这样一种目的为前提，阐述如何判断施用化学杀虫剂的最佳时期。

1 模型定义

假如设定一种昆虫有i=1～6个发育时期，包括卵、第一龄若虫、第二龄若虫、第三龄若虫、伪蛹和成虫。比如，黑刺粉虱 [Aleurocanthus spiniferus（Quaintance）]，假定越冬代的伪蛹数量（O）和净增长率（R）。不同发育时期在田间的自然死亡率为Pi（i=1～6），不同发育时期施用杀虫剂后的死亡率为Qi（i=1～6）。这样，在没有施用杀虫剂的情况下，第一代伪蛹的种群数量（Y）应该可以表示为：

而只在昆虫的第i个发育阶段施用杀虫剂的情况下，第一代伪蛹的种群数量（Yi）应该可以表示为：

要使防治效果最好，就应该使得第一代伪蛹的数量最小。在方程式（1）中Y是一个常数，令Ai=，则当 Ai最小时，Yi得到最小值 Ymin表示为如果一个参数或者一个函数式例如Qi、Pi、（Qi-P）i和Pi/Qi跟函数Ai有一一对应的关系，那么就可以通过这些参数或函数式代替Ai决定Ymin。很显然，当Qi为常数，函数 Ai会随着Pi的增大而增大，当 Pi为常数 ，Ai将随着 Qi的增大而变小。因此，参数Qi或者Pi都跟Ai没有一一对应的关系，不能代替Ai决定Ymin。假设（Qi－Pi）为常数 “b”（>0）,则当 Pi增大到 P1时，Qi也相应的增大到 Q1，公式表示为：b=Qi－Pi=Q1－P1。

如果 X1被定义为 X1=Q1－Qi=P1－Pi，那么：

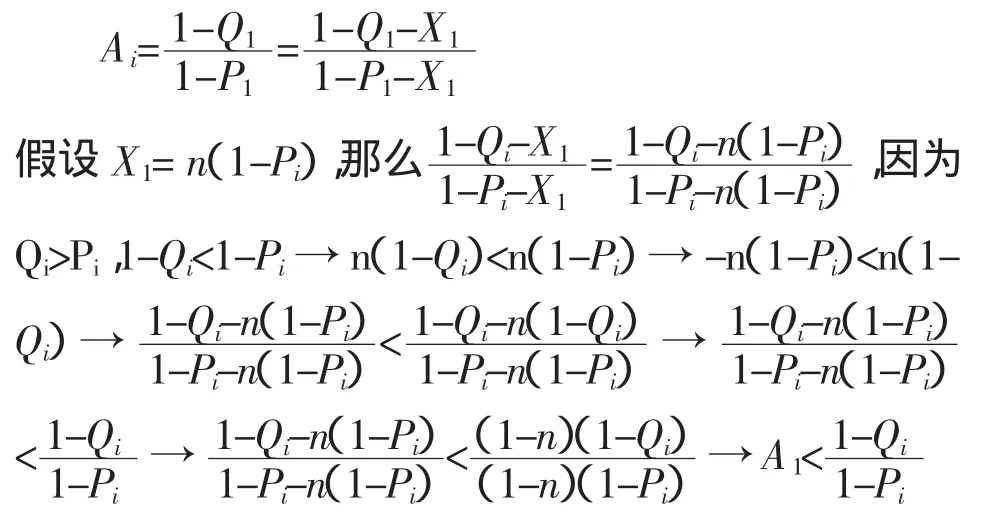
以上推导过程显示，若（Qi－Pi）为常数b（b＞0），Ai将随着Pi或Qi的增大而增大。因此，函数（Qi－Pi）跟Ai也不存在一一对应关系，即不可以通过该函数决定 Ymin。

假设函数 Pi/Qi是常数“c”（c＞0），则当 Pi增大到P2，那么 Qi也必须相应的增大到 Q2，即：c＝Pi/Qi＝P2/Q2和 P2/Pi＝Q2/Qi。如果 X2被定义为：X2=P2/Pi＝Q2/Qi，那么

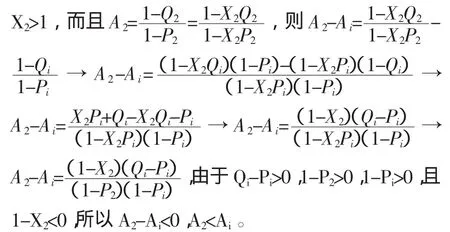
上述推导显示 Pi/Qi为常数“c”（c＞0）时，Ai将随着Pi或Qi的增大而减小。所以，函数Pi/Qi跟Ai也不存在一一对应关系，也不能通过Pi/Qi决定Ymin。简而言之，参数Qi或Pi和函数（Qi－Pi）或Pi/Qi都跟Ai不存在一一对应关系，也就不能用来决定Ymin。同时，这些参数或函数中的任何两个都可以一起被用来代替Ai决定Ymin，因为这些参数或函数中的任何两个都可以组成一个具有唯一解的方程组。如果它们中的任何一个不变，则当Qi或（Qi－Pi）增大时，Ai减小；当Pi或Pi/Qi增大时，Ai也增大。

2 结果与分析

在许多杀虫剂的生产应用试验里，校正死亡率常被用来判定杀虫效果，而校正死亡率的计数范围往往只包括相邻的两个虫态[9-11]。这样判断杀虫剂的效果，在每个虫态自然死亡率都一样的情况下是可以的，但有其局限性，因为不同的发育阶段会有不同的自然死亡率和不同的药剂敏感性。笔者提出的模型中，函数Yi被用来判断杀虫剂的田间应用效果只考虑了一个完整的世代。应用该判断标准可以很好地的解释在笔者的试验中，下一代黑刺粉虱种群密度减少最快的处理不是校正死亡率最大时施药的处理（数据未列出）。

而一些参数或函数，如Qi、Pi、（Qi－Pi）或Pi/Qi被用来判断最佳施药时期（虫态）的标准，也有他们各自的优点和局限性。函数Ai被用来判断最佳施药时期（虫态）是很准确的，可是计算却比较麻烦。有些昆虫，只有特定的虫态才容易被抽样调查，此时也会采用自然死亡率（Pi）作为判断最佳施药时期（虫态）的依据。有些药剂，在田间对昆虫特定的虫态进行药剂处理后，死亡率很高，此时，药剂处理死亡率（Qi）也用来作为判断最佳施药时期（虫态）的依据。而某些药剂只对昆虫的某个特定虫态有作用，此时，校正死亡率（Qi－Pi）也被用作判断最佳施药时期（虫态）的依据。自然死亡率和药剂处理死亡率的比值 最接近Ai，可是，这个比值在试验结果当中却并不直观。

许多生态模型都可以用来解释试验结果，但是这些模型在更进一步的外延时，大多会遇到这样或那样的问题。同样的道理，方程式（1）也遇到了类似的问题，比如有些杀虫剂对昆虫害虫的几个世代都有持效作用，或者有些昆虫的世代在田间呈现重叠的现象，这样使用该模型作为判断最佳施药虫态的标准也会出错或者难以实施。

总之，笔者提供的模型可以作为判断最佳施药时期（虫态）的方法。但是，当杀虫剂施用之后的作用不仅对目前的虫态有致死作用，而且对发育到后期的虫态的死亡率也有影响，或者昆虫世代严重重叠时，该模型还有待进一步的完善。

[1] 仇贵生，李美娜，张 平，等.苹果主要病虫害的预测预报、防治适期及药剂选择[J].中国植保导刊，2006，26（6）：31-33.

[2] 李学军，王淑贤，郑 国，等.辽宁朝阳地区高粱蚜田间消长规律及防治适期[J].昆虫知识，2007，44（1）：53-57.

[3] 吕 欣，曾 琳，陆永跃，等.杨桃园桔小实蝇的防治适期研究[J].环境昆虫学报，2008，30（3）：214-219.

[4] 刘守柱，杜学林，戴明勋.20%啶虫脒对黄瓜蚜虫的防治效果[J].湖南农业科学，2010，（3）：77-79.

[5] 杨少波，吴克桂.园艺场柑桔主要病虫害发生及防治[J].广东农业科学，2009，（7）：135-136.

[6] 龙亚芹，王万东，王美存，等.云南小规模芒果种植模式和病虫害防治调查[J].江西农业学报，2010，（11）：105-107.

[7] Nilima P，Castle S J，Toscano N C.Susceptibility of immature stages of Homalodisca coagulate （Hemiptera:Cicadellidae）to selected insecticides[J].Journal of Economic Entomology，2006，99（5）：1805-1812.

[8] Brown M W.Applying principles of community ecology to pest management in orchards[J].Agriculture,Ecosystems&Environment，1999，73（2）：103-106.

[9] 李 明，曾 唏，季祥彪，等.盐酸黄连素对蚜虫生物活性的研究[J].昆虫学报，1999，42（2）：140-144.

[10] 蒋拥东，周芳芳，陈功锡.吉首寨阳大棚草莓病虫害调查及防治措施[J].湖南农业科学，2010，（12）：90-91，95.

[11] Wang Y H，Gao C F，Xu Z P，et al.Buprofezin susceptibility survey,resistance selection and preliminary determination of the resistance mechanism in Nilaparvata lugens （Homoptera:Delphacidae） [J].Pest Management Science，2008，64（10）：1050-1056.