雷诺数效应对斜拉索风致振动的影响

刘庆宽，王 毅，郑云飞，马文勇

（石家庄铁道大学 风工程研究中心，石家庄050043）

由于斜拉桥斜拉索的长细比大、阻尼低等特点，导致在大风或风雨联合作用下经常发生大幅振动，对桥梁结构的安全造成危害。与传统的振动类型相比，风雨激振和干索驰振（Dry Cable Galloping）由于振幅大、破坏严重，是值得深入研究的问题。关于风雨激振，自20世纪80年代被发现以来，各国学者通过现场观测与风洞试验［1－4］、理论分析［5－7］及 CFD等手段已经进行了较广泛的研究，针对其振动机理提出了水线驰振理论、高风速涡致振动理论、轴向流理论、弯扭两自由度耦合理论、水线摆动理论、卡门涡被抑制导致大幅振动等理论，建议采用的气动抑振措施有缠绕螺旋线和索的表面设置凹坑［8］等。

在斜拉索风雨振的现场观测［9－10］、足尺模型观测［11］，风洞试验［12－13］研究中，研究人员发现在没有降雨、或者降雨量很小不足以形成水线、或降雨已经停止的状态下，斜拉索也可能发生大幅振动，尤其是日本Sunbridge桥的斜拉索发生大幅振动［10］以来，这种振动现象及其机理引起了高度重视。目前Cheng 等［14］利 用 Den Hartog 驰 振 理 论、Matsumoto［15］利用卡门涡的脱落抑制理论等对干索驰振的机理进行了解释，但是无论其发生的机理、还是与风雨激振的内在关系，以及抑振措施等，都需要进一步的深入研究。

该文从雷诺数效应入手，通过测力和测振风洞试验，以不同雷诺数下的阻力系数、升力系数和振幅为参数，研究了雷诺数效应是否导致振动、不同粗糙度表面模型的雷诺数效应及与振动的关系、水线影响雷诺数效应及通过影响雷诺数效应导致振动的机理。

1 试验介绍

为了研究斜拉索的雷诺数效应和气动稳定性的关系，共进行了2大类的风洞试验，其一是两端固定刚性模型的测力试验，其二是两端弹簧支撑刚性模型的测振试验，试验对象分别是表面粗糙度不同、没有人工水线的斜拉索模型和表面光滑的贴有人工水线的斜拉索模型。试验在石家庄铁道大学风工程研究中心的双试验段回／直流大气边界层风洞内进行，其低速试验段转盘中心宽4．4 m，高3．0 m，长24．0 m，最大风速大于30．0 m／s，背景湍流度I≤0．4%；高速试验段宽2．2 m，高2 m，长5．0 m，最大风速大于80．0 m／s，背景湍流度I≤0．2%。风洞结构如图1所示［16］。本试验在高速段内进行。

图1 风洞平面图

为了实现不同雷诺数下的雷诺数效应，使用了4个刚性斜拉索模型，具体参数如表1所示。

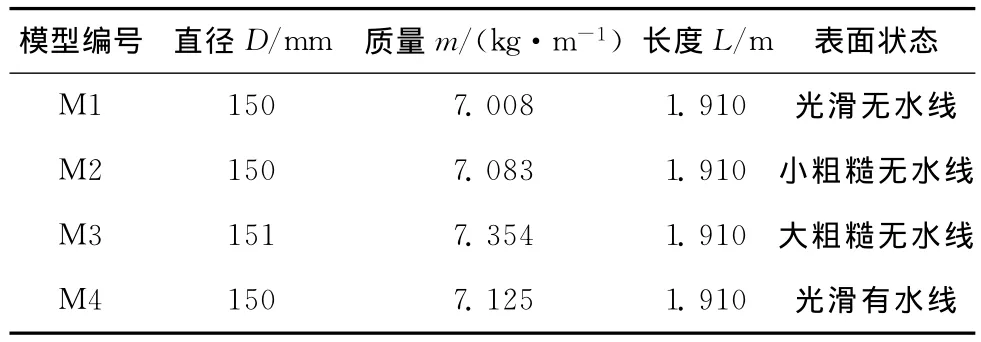
表1 模型参数

模型的材质为有机玻璃，原型为表面光滑的圆柱，两端设置端板，由中间贯穿的刚性圆管支撑在风洞两侧的支架上。M1模型为光滑表面，M2模型是将光滑圆管用P24号砂纸均匀打磨而成，M3模型是将光滑圆管用表面粗糙的壁纸包裹而成，M4模型是在M1模型的基础上分别在不同的位置粘贴人工水线而成。对于人工水线，利用有机塑料加工成圆弧外形，粘贴在斜拉索的表面。斜拉索表面和水线的形状如图2所示（为了对比表面的粗糙度，拍照时模型表面放置了最大直径约7 mm铅笔）。水线的位置用θ表示，是从前驻点到水线中心转过的圆心角。

测力模型为两端固定支撑，端部安装美国ATI公司生产DELTA系列六分力高频天平，测试采样时间为60 s。

测振模型两端分别用4根弹簧支撑，弹簧刚度的选取以系统的振动频率与实际相同直径斜拉索的振动频率一致为原则。为了便于起振，模型系统的Sc数比实际斜拉索的稍小。振动过程中记录瞬态位移。

图2 模型表面状态和水线尺寸

测力和测振模型的空间位置为：竖直倾斜角α＝0°，水平倾斜角β＝0°，即斜拉索模型在水平面内，与来流风向垂直。

试验中的控制风速由安装在试验段入口的传感器与控制台组成的稳风速控制系统控制，模型处的来流风速澳大利亚Turbulent Flow Instrumentation公司生产的4孔眼镜蛇探头（4－hole Cobra Probe）测试，安装位置为模型中心上游1．05 m、下方0．47 m处，采样频率2 000 Hz，测力的采样时间60 s，测振的记录时间为整个振动观察的时间范围。

因为不同粗糙度模型对应的临界雷诺数不同，所以4个模型的试验雷诺数范围不同，并且为了准确反应力系数的变化情况，针对各个模型的临界雷诺数区域分别加密了测试工况。

水线位置从10°开始，以2．5°为步长增加到70°。为了从机理上进行研究，采用的水线位置比实际可能形成水线的位置范围要大。3个无水线模型对应的试验雷诺数范围、步长如表2所示，有水线模型的试验工况如表3所示。

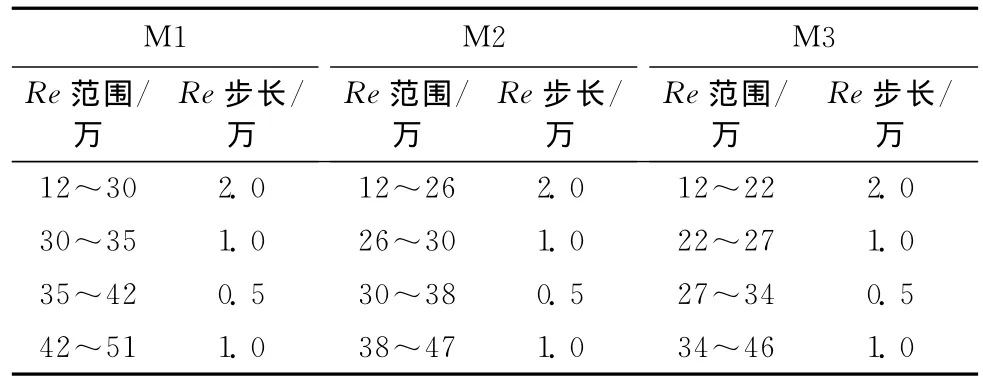
表2 无水线模型（M1—M3）测力和测振试验工况

表3 有水线模型（M4）测力和测振试验工况

2 无水线模型雷诺数效应对气动稳定性的影响

2．1 无水线模型的雷诺数效应

使用3个不同粗糙度模型测得的平均阻力系数和平均升力系数随雷诺数的变化曲线如图3所示。由图可知，在临界雷诺数区域，模型的平均阻力系数下降，平均升力出现。平均升力开始出现时的雷诺数，基本对应平均阻力系数开始下降时的雷诺数；平均阻力系数大约下降到整个下降幅度一半的时候，平均升力系数取得最大值，之后随着雷诺数的增大平均升力系数开始减小，当平均阻力系数下降到最小值的时候，平均升力系数基本恢复到零值。

图3 平均阻力系数和平均升力系数曲线

随着模型表面粗糙度的增加，平均阻力系数的下降幅度减小，平均升力系数的最大值减小，即雷诺数效应减弱。同时，随着粗糙度的增加，临界雷诺数区域整体向低雷诺数方向移动了一定数值，即在较小的雷诺数数值时就进入了临界雷诺数的状态。

2．2 无水线模型的气动稳定性

无水线模型的测振结果如图4所示。对照图3可以发现，各个模型在亚临界雷诺数区域，振动的振幅都很小，可以认为是稳定的；雷诺数到达临界区域时，振幅显著增大，光滑斜拉索模型的最大振幅达到了12．3 cm，0．82D（其D为斜拉索的直径），超过临界雷诺数区域之后，振幅又下降至很小，基本可以认为是恢复到了稳定状态。最大升力系数出现时的雷诺数，对应最大振幅。随着模型表面粗糙度的增加，在临界区域发生振动的振幅减小。结合图3综合分析可以推知，在临界雷诺数区域，由于阻力系数的减小和升力的出现、流场从卡门涡周期脱落状态变为不规则的状态等因素，导致了振动的发生，但是振动发生具体的机理尚待流场分析等进一步的研究。

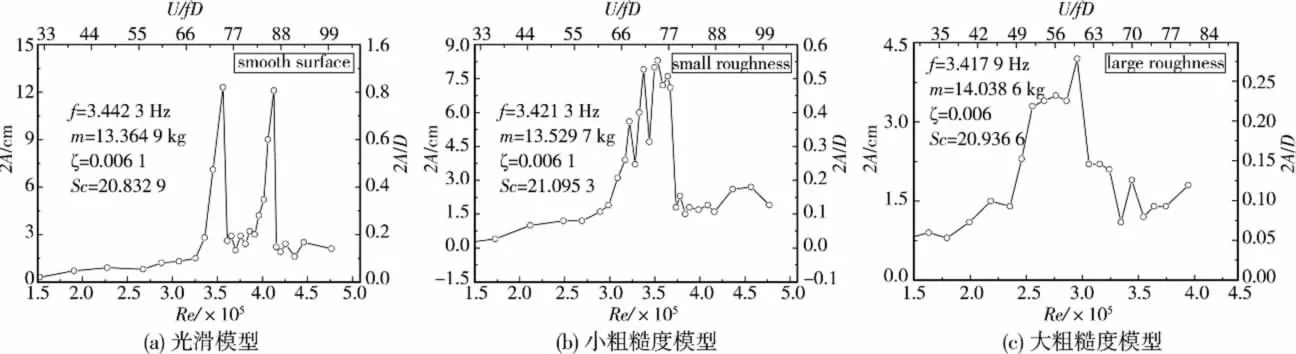
图4 振幅与雷诺数曲线

3 有水线模型雷诺数效应对气动稳定性的影响

3．1 水线对雷诺数效应的影响

对粘贴有人工水线的斜拉索模型的阻力系数、升力系数、自由振动振幅分别进行了测试，利用阻力系数和升力系数，计算如公式（1）所示的表达式的值，即Den Hartog驰振准则。如果值为负，则可能发生驰振。

分析表明：随着雷诺数从小到大的变化，水线位置不同，阻力系数、升力系数的变化也不同，相应的dCF／dα的值和自由振动的状态也不同。选取水线位置θ＝15°、25°、55°3个有代表性的工况进行分析，其阻力系数和升力系数分别如图5—7所示。

由图5可知，水线位置θ＝15°时，阻力系数从Re＝17万左右开始随着Re的增长呈现阶段性下降趋势，其中25万至37万之间基本保持不变，从37万开始急剧下降，一直到Re＝43万左右降到最低；与此对应，升力系数从Re＝17万左右开始上升，在Re＝25万和37万之间保持较大值，之后急速下降，到Re＝43万左右基本降到最低。

从Re＝17万到43万之间阻力系数下降、出现较大升力的现象，与光滑模型的临界雷诺数区域的特征一致，可以判断这个区域为临界雷诺数区域。对照图3（a）的结果可知，2个工况临界雷诺数区域结束时的雷诺数（43万）基本一致，而水线的存在，大大提前了临界雷诺数区域开始时的雷诺数数值（无水线时35万，15°水线时17万）。

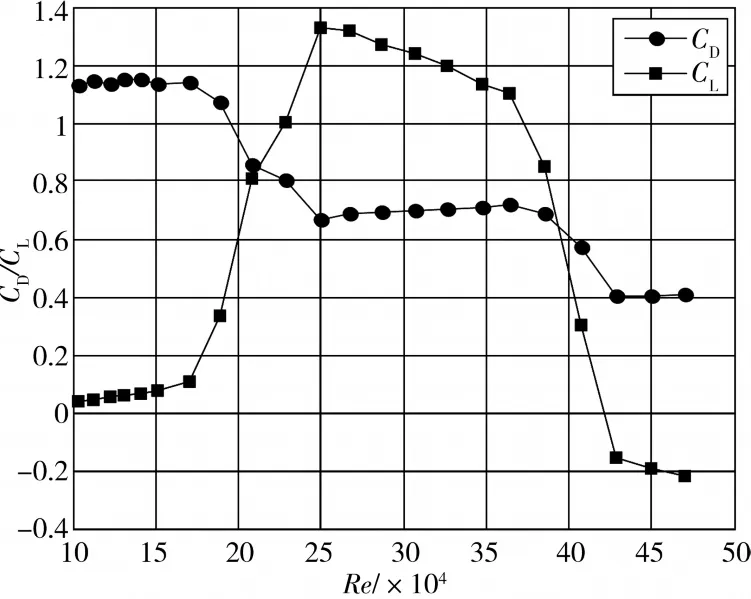
图5 水线位置15°的阻力系数和升力系数

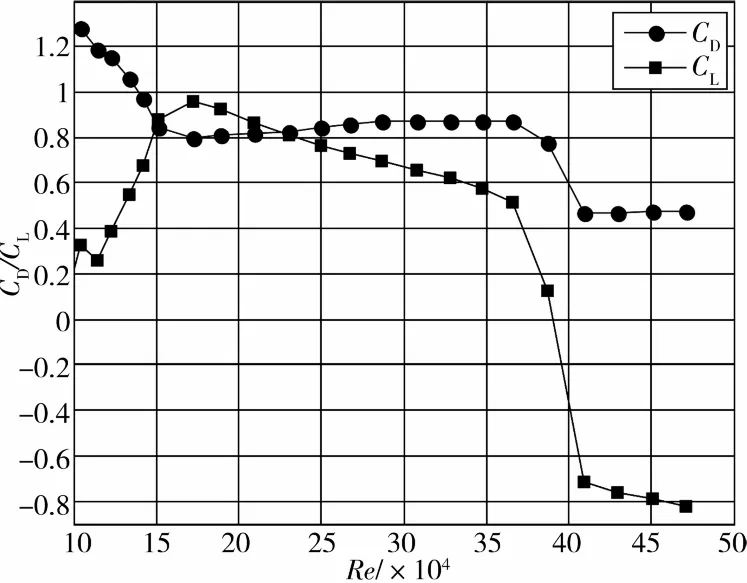
图6 水线位置25°的的阻力系数和升力系数

比较25°和15°时的阻力和升力系数（图6、图5）可知，25°水线时临界雷诺数区域的升力系数整体比比15°时的小（25°水线时升力系数最大值在1．3～1．1之间，15°的在1．0～0．5之间），相同阶段的阻力系数比15°时的大，临界雷诺数效应开始时的雷诺数数值比15°时的小，力系数降到最低时的雷诺数（41万）比15°时（43万）的小。

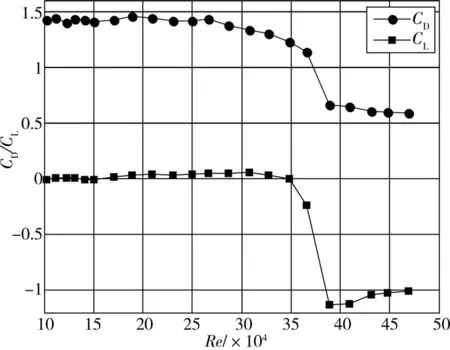
图7 水线位置55°的的阻力系数和升力系数

比较55°水线时的情况可知，在Re＝10～35万范围内，升力系数基本为零值，阻力系数保持在1．5左右，从图上已经看不到升力系数上升阻力系数分阶段下降的情况。从35万开始，2个力系数急剧下降，39万左右基本降到最低。

综上，可以总结出力系数随水线升高的变化特征为：力系数急剧下降基本出现在Re＝35万，随着水线位置的升高，力系数降到最低时的雷诺数数值逐渐减小，临界雷诺数区域对应的升力系数逐渐减小，阻力系数逐渐增大，临界雷诺数效应发生的范围扩大。即水线位置不同，阻力系数、升力系数的大小、变化规律和雷诺数效应不同。

3．2 水线对气动稳定性的影响

粘贴有人工水线的斜拉索模型各个雷诺数下的dCF／dα值和测振结果如图8—10所示。

随着水线位置的变化，阻力系数和升力系数的变化有可能导致dCF／dα＜0，发生驰振。

由15°水线的dCF／dα和振动图（图7）可知，Re在27万到28万之间，dCF／dα由正变负，在该雷诺数附近模型开始发生大幅振动，dCF／dα为负的区域与发生大幅振动的区域基本一致。

水线位置为25°时，虽然从Re＝15万之后dCF／dα一直为负值，但是大幅振动却分别发生在2个雷诺数区域，一个是Re＝15～25万之间，另一个是Re＝37～42万之间。前一个区域的发生机理，可能是单纯由于水线位置上下变动时阻力系数、升力系数的数值不同，因而dCF／dα＜0引起，后一个区域发生振动的机理，结合无水线时力系数突然下降时发生大幅振动的结果（图3（a）和图4（a）），推断除了dCF／dα＜0之外，是否可能与力系数的急剧下降和流场的不稳定有关，该机理尚需要进一步研究才能明确。

水线位置为55°时发生振动的状况同25°时类似，也是发生在2个区域，只不过在力系数急剧下降时，发生大幅振动的区域变窄。2个区域振动的机理分析同25°工况。

图8 水线位置15°的d C F／dα和振动振幅

图9 水线位置25°的d C F／dα和振动振幅

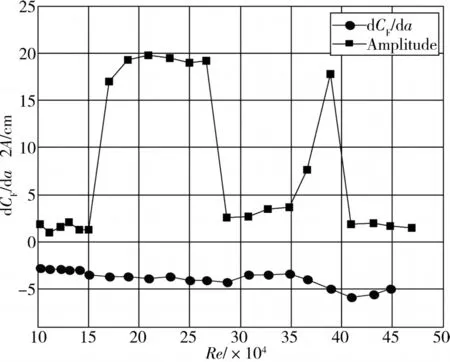
图10 水线位置55°的d C F／dα和振动振幅

4 结论

利用不同粗糙程度无人工水线的斜拉索模型和光滑表面贴有人工水线的斜拉索模型，通过测力和测振风洞试验，得到了斜拉索模型气动力、气动稳定性的结果。通过分析相关的关系，得到了以下结论：

1）在临界雷诺数区域，力系数及周围流场的变化特性可能导致斜拉索发生大幅振动，这可能是干索驰振的机理。

2）随着斜拉索表面粗糙度的增加，临界雷诺数区域整体向小的方向移动，雷诺数效应减弱，在临界雷诺数区域发生振动的振幅减小。

3）水线的存在能改变雷诺数效应，一些水线位置在特定的雷诺数范围内，由于力系数的特殊变化规律导致dCF／dα为负，斜拉索发生了符合驰振判据的振动。

4）在高雷诺数区域，斜拉索发生振动的机理除dCF／dα为负之外，还可能与力系数急剧下降及流场的不稳定有关，该部分机理尚需进一步的研究进行明确。

［1］MACDONALD J H G，LAROSE G L．Two－degree－offreedom inclined cable galloping－Part 1： General formulation and solution for perfectly tuned system［J］．Journal of Wind Engineering and Industrial Aerodynamics，2008，96（3）：291－307．

［2］MACDONALD J H G，LAROSE G L．Two－degree－offreedom inclined cable galloping－Part 2：Analysis and prevention for arbitrary frequency ratio［J］．Journal of Wind Engineering and Industrial Aerodynamics，2008，96（3）：308－326．

［3］刘庆宽．斜拉桥斜拉索风雨振时索表面水线摆动作用及规律的试验研究［J］．土木工程学报，2007，40（7）：62－67．LIU QING－KUAN．Experimental study on movement of water rivulet on cable surface in rain－wind induced vibration of stay－cables［J］．China Civil Engineering Journal，2007，40（7）：62－67．

［4］李永乐，卢伟，陶齐宇，等．斜拉桥拉索风－雨振动特性风洞试验研究［J］．试验流体力学，2007，21（4）：36－40．LI YONG－LE，LU WEI，TAO QI－YU，et al．Study on rain－wind induced vibration of cables in cable－stayed bridges by wind tunnel test［J］．Experiments and Measur in Fluid Mechanics，2007，21（4）：36－40．

［5］李寿英，顾明，陈政清．运动水线三维连续弹性拉索风雨激振理论模型［J］．湖南大学学报：自然科学版，2009，36（2）：1－7．LI SHOU－YING，GU MING，CHEN ZHENG－QING．An analytical model of rain－wind－induced vibration of three－dimensional continuous stay cable with actual moving rivulet［J］．Journal of Hunan University：Naturnal Science，2009，36（2）：1－7．

［6］张琪昌，李伟义，王炜．斜拉索风雨振的动力学行为研究［J］．振动与冲击，2010，29（4）：173－176．ZHANG QI－CHANG，LI WEI－YI， WANG WEI．Nonlinear dynamic behavior of rain－wind－induced vibration of a stay cable［J］．Journal of Vibration and Shock，2010，29（4）：173－176．

［7］李暾，陈政清，李寿英．连续弹性拉索风雨激振理论模型研究［J］．振动工程学报，2010，23（4）：380－388．LI TUN，CHEN ZHENG－QING，LI SHOU－YING．Analytical study of rain－wind－induced cable vibrations based on continuous elastic cable model［J］．Journal of Vibration Engineering，2010，23（4）：380－388．

［8］刘健新，李哲．气动措施对斜拉索风荷载及结构响应的影响［J］．建筑科学与工程学报，2010，27（3）：89－93．LIU JIAN－XIN，LI ZHE．Influence of aerodynamic measure on wind load and structural response of stayedcable ［J］． Journal of Architecture and Civil Engineering，2010，27（3）：89－93．

［9］VIRLOGEUX M． Cable vibrations in cable－stayed bridges ［C ］／／Bridge Aerodynamics． Balkema：Rotterdam，1998：213－233．

［10］MATSUMOTO M．The role of water rivulet on inclined cable aerodynamics［C］／／Proceedings of the 6th Asia－Pacific Conference on Wind Engineering．Seoul，Korea，2005：63－77．

［11］MATSUMOTO M，SHIRATO H，YAGI T，et al．Field observation of the full－scale wind－induced cable vibration［J］． Journal of Wind Engineering and Industrial Aerodynamics，2003，91（1／2）：13－26．

［12］MATSUMOTO M，YAMAGISHI M，AOKI J，et al．Various mechanism of inclined cable aerodynamics［C］／／Proceeding of 9th International Conference on Wind Engineering，New Delhi，India，1995：759－770．

［13］CHENG S，LAROSE G L，SAVAGE M G，et al．Experimental study on the wind－induced vibration of a dry inclined cable－Part I：Phenomena［J］．Journal of Wind Engineering and Industrial Aerodynamics，2008，96（12）：2231－2253．

［14］CHENG S，IRWIN P A，TANAKA H．Experimental study on the wind－induced vibration of a dry inclined cable－Part II：Proposed mechanisms［J］．Journal of Wind Engineering and Industrial Aerodynamics，2008，96（12）：2254－2272．

［15］MATUMOTO M，YAGI T，HATSUDA H，et al．Dry galloping characteristics and its mechanism of inclined／yawed cables［J］．Journal of Wind Engineering and Industrial Aerodynamics，2010，98（6／7）：317－327．

［16］刘庆宽．多功能大气边界层风洞的设计与建设［J］．实验流体力学，2011，25（3）：66－70．LIU QING－KUAN．Aerodynamic and structure desigh of multifunction boundary－layer wind tunnel ［J］．Journal of Experiments in Fluid Mechanics，2011，25（3）：66－70．