层次-粗集组合赋权法在雷达辐射源识别中的应用＊

姚 珅，高贵明

(1.南京信息工程大学 电子与信息工程学院，南京 210044;2.南京船舶雷达研究所，南京 210003)

1 引言

雷达辐射源识别技术是目标识别技术的重要组成部分。在军事作战中，发现目标主要依靠雷达探测。雷达探测会辐射电磁波，我方可通过电子侦察设备被动地接收并捕获敌方雷达发射的电磁波，并快速提取出辐射源信号的频率、调制方式等参数。依据这些参数，按照某种规则和算法及查询辐射源特征数据库，进而确定雷达辐射源的体制、用途、型号等信息，为上级决策机构提供情报支持，做到先发制敌，取得战场的主动权［1］。

目前在进行雷达辐射源识别时，通常采用等权或专家直接赋值法对待匹配特征参数进行权系数确定，而这些方法主观性太强，很多时候并不符合客观实际情况，没有充分发挥重要性程度较高的参数应有的作用。分析显示，等权和专家直接赋值法在面对不同的识别库时识别率波动较大，稳定性较差［2］。本文详细分析了层次分析法和粗糙集理论，认为这两种方法具有互补性，从而提出层次-粗集组合赋权法，实现二者的优势互补，提高对辐射源识别参数赋值的可靠性、科学性和客观性。

2 层次分析法

层次分析法(Analytic Hierarchy Process，AHP）是由美国著名运筹学家T.L.Satty 等人于20 世纪70年代提出的一种定性、定量相结合的决策与评价方法［3］，其基本思想是将复杂问题分解为各个组成因素，又将这些因素按支配关系分组形成层次结构，以人们的经验判断为基础，通过两两比较的方式确定各个因素相对重要性，然后通过计算确定决策方案相对重要性的总排序。其实质是利用1～9的整数及其倒数作为标度构造判断矩阵。用层次分析法处理问题需经过以下4个步骤:

(1）分析问题，建立层次结构模型。弄清问题所包含的因素(目标、准则、约束、可能情况、方案）及各因素间的关联，按照目标层、准则层和方案层的形式排列起来。

(2）构造判断矩阵。将每一层次各个因素有关联的下一层次诸因素的相对重要性做出判断，根据表1所示的9 级标度将判断结果定量化，从而构成判断矩阵。例如，要比较某一层n个因素，每次取其中两个Bi和Bj进行比较并按表1 表示为aij，全部结果用矩阵表示，即A=(aij）n×n，aij×aij=1。

表1 判断矩阵标度表

(3）层次单排序及一致性检验。它是根据判断矩阵计算对于上一层某因素而言，本层次与之有联系的因素的重要性次序的权值。常用的计算方法有方根法、和法、特征根法、最小二乘法等。

(4）层次总排序及一致性检验。它是同一层次所有因素对最高层相对重要性的排序权值，通过一致性检验后得到择优结果。

AHP 能将复杂问题层次化，将定性问题定量化。通常情况下，AHP 权系数有着很不错的识别率。虽然该方法能充分吸收专家的知识和经验，体现出各个目标的重要程度，但仅凭经验得出的结果往往具有较大程度的主观性，且这一弊端并不会因为采取增加专家数量、严格挑选专家等措施而得到根本改善。当库中样本数据较多、数据间的内在规律比较明显时，客观赋值方法所得权系数可能比AHP 权系数更符合实际。

3 粗糙集理论

粗糙集(Rough Set）理论是由波兰学者Z.Pawlak于1982年提出的一种新的处理模糊和不确定性知识的数学工具。粗糙集理论以其特有的属性约简和属性重要度原理，无需任何先验信息，根据观测数据剔除冗余信息，并比较不同属性间的依赖性与重要性，导出分类或决策规则［4］。

3.1 粗糙集理论相关概念［5］

定义1 四元组S=(U，A，V，f）是一个信息系统，其中U 表示对象的非空有限集合，为论域;A 表示所有属性的非空有限集合;V=∪a∈AVa，Va是属性a的值域;f表示U×A→V 是一个信息函数，它为每个对象的每个属性赋予一个信息值。

定义2 每一个属性子集P⊆A 决定了一个二元等价关系IND(P）:

IND(P）={(x，y）∈U×U|∀a∈P，f(y，a）。若(x，y）∈IND(P），则x和y 是P 不可分辨的。

定义3 等价关系IND(P）构成了U的一个划分，用U/IND(P）={X1，X2，…，Xn}表示，其中Xi表示不同的等价类。在IND(P）下与x 不可分辨的所有对象构成一个等价类，记为［x］IND(P）。

定义4 信息系统S=(U，A，V，f），属性a∈A，如果IND(A－{a}）=IND(A），则a 在A中是不必 要的;否则a 是必要的。

定义5 信息系统S=(U，A，V，f），如果任意a∈A在A中都是必要的，则属性集A 是独立的;否则A 是相关的。

定义6 设S=(U，A，V，f）是一个信息系统，如果P⊆A，IND(P）=IND(A）且P 是独立的，则P 是A的一个约简。

定义7 信息系统S=(U，A，V，f），A中所有必要的属性组成的集合为属性集A的核，记为CORE(A）。

可以证明核是所有约简的交集。

定义8 信息系统S=(U，A，V，f），P⊆A，U/IND(P）={X1，X2，…，Xn}。P的信息熵定义为

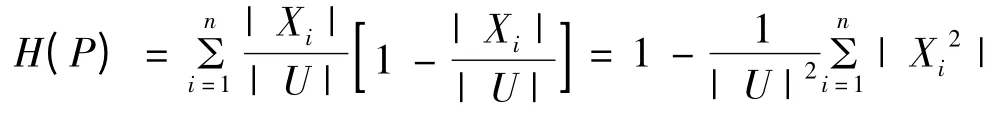
其中|X|表示集合X的基数。

定义9 信息系统S=(U，A，V，f），属性a∈A 在A中的重要度定义为

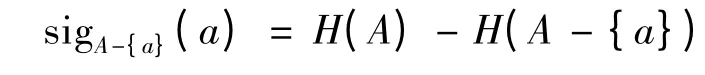
上述定义表明，属性a∈A 在A中的重要度是由A中去掉{a}后所引起的信息熵变化的大小来度量的。

定义10 信息系统S=(U，A，V，f），属性集C⊆A，任意属性a∈A－C 关于C的重要度定义为

上述定义表明，属性a∈A－C 关于属性集C的重要度由C中添加a后所引起的信息熵变化的大小来度量。

定义11 信息系统S=(U，A，V，f），A={a1，a2，…，aa}属性ai∈A 在A中的重要度为sigA－{ai}，则其权重定义为

3.2 属性约简［6］

粗糙集的属性约简，就是在保持属性集分类能力不变的情况下，剔除不相关或不重要的信息，删除冗余属性。现阶段存在的约简算法主要包括利用不可分辨关系、属性重要度、差别矩阵、集合近似质量等性质开发的属性约简算法。本文利用属性重要度进行属性约简，算法主要步骤如下。

输入:信息系统S=(U，A，V，f）。

步骤1 根据定义8 计算信息系统的信息量H(A）。

步骤2 令CORE=Φ，对于任意ai∈A，根据定义9 计算其重要度sigA－{ai}(ai），若sigA－{ai}(ai）不为0，则使CORE=CORE ∪{ai}。计算H(CORE），若H(CORE）=H(A），计算终止(此时CORE为A的最小近似约简）;否则执行步骤3。

步骤3 令C=CORE，对指标集A－C 重复执行:

(1）对于每个指标ai∈A，根据定义10，计算其重要度sigC(ai）;

(2）取max sigC(ai），C=C∪{ai};

(3）若H(C）=H(A），计算终止(此时C为A的一个最小近似约简）;否则，转(1）。

输出:该信息系统的核CORE和最小约简C。

3.3 基于重要度的判断矩阵［7］

对于属性约简后的信息系统，可以得到约简的指标集C={r1，r2，…，rn}。任意ri∈C，根据定义9，计算重要度sigC－{ri}(ri）。采用两两比较的方法，可以构造类似于层次分析法中的判断矩阵:bij=sigC－{ri}(ri）/sigC－{rj}(rj），即B=(bij）n×n。

利用重要度计算得到的判断矩阵是以属性自身的信息为依据，对数据本身进行挖掘，真实反映了事物的内在规律，很好地避免了确定权重时受主观因素的影响。

4 层次-粗集组合赋权法

粗糙集理论能充分利用数据库中已有信息来进行权系数的确定，是不错的客观赋值方法。但是，当样本数据较少时，很难找到数据间的内在规律，此时所得权系数对应的识别率可能不如主观赋值法。因此，本文综合层次分析法和粗糙集理论来确定权系数，采用组合赋值思想，以期获得更为合理的权系数。这就是层次-粗集组合赋权法。该方法主要步骤如下:

步骤1 构建信息系统S=(U，A，V，f）;

步骤2 根据粗糙集理论的属性约算法，对所给出的属性进行约简;

步骤3 对于属性约简后的信息系统，分别利用层次分析法及粗糙集重要度赋权法构造判断矩阵A=(aij）n×n和B=(bij）n×n;

步骤4 将两个判断矩阵进行组合，通过建立最优化模型，可得两者的组合矩阵:C=μA+(1－μ）B，其中0≤μ≤1。

步骤5 对组合矩阵C 进行权重计算，求出各属性的权重向量W=［w1，w2，…，wn］。

针对雷达辐射源识别的应用背景，作几点说明:

(1）数据库中各型号雷达作为对象集合U，待匹配的特征参数作为信息系统的属性集合A，各型号雷达特征参数的取值即为每个属性a的取值Va，从而构建一个信息系统S。

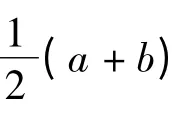
(3）雷达辐射源信号由于受噪声等多种因素影响，最重要的特征常常难以发现。特征提取一般采用经验式或启发式方法，所提取出的特征往往带有主观性和猜测性。为了消除特征提取的主观性和提高正确识别率，需要采用特征选择方法，从高维特征中挑选最有效的特征集。粗糙集的属性约简实现了这样的一种作用，从若干雷达辐射源信号特征组成的原始特征集中去除冗余特征，发现最重要的特征子集。

(4）在雷达辐射源识别实际应用中，在分析的初始阶段，由于样本数据较少，数据间内在规律还没有形成，应注重专家的经验知识;随着样本数据的不断积累，可以利用特征参数的内在规律来确定权系数。因此，对于组合矩阵C=μA+(1－μ）B，当0≤μ≤0.5时决策倾向于专家经验，当0.5≤μ≤1时决策倾向于客观数据。本文μ 取0.38，使主客观矩阵系数比为黄金分割数。

5 仿真分析

本仿真过程主要利用本文提出的方法(简称组合法）与层次分析法和单纯粗糙集理论得出的权系数，对识别率的影响进行比较分析。识别数据库有两个:一个含100 部雷达数据(由多种体制构成），称库1;另一个含10 部雷达数据(频率捷变体制），称库2。

利用粗糙集属性约简进行特征选择可获得各数据库用于匹配识别的特征参数，库1 对应的参数为载频、重频和脉宽;库2 对应的参数为载频、重频、脉宽、周期分割数、间隔脉冲数和最大频偏。分别利用3 种赋权法对这两个数据库所得权系数赋值，如表2所示。识别时首先选择库中某一雷达型号，对该型号相应特征参数值加上符合正态分布的噪声。然后利用特征参数匹配法将其和库中所有雷达型号进行匹配求解匹配置信度，最后按决策规则即可识别出雷达型号，比较识别型号和所选雷达型号是否相同来确定识别率。

图1为3 种赋权法所得权系数在不同噪声下的识别率情况，识别采用的方法为梯形曲线模糊匹配法。

表2 3 种赋权法所得权系数

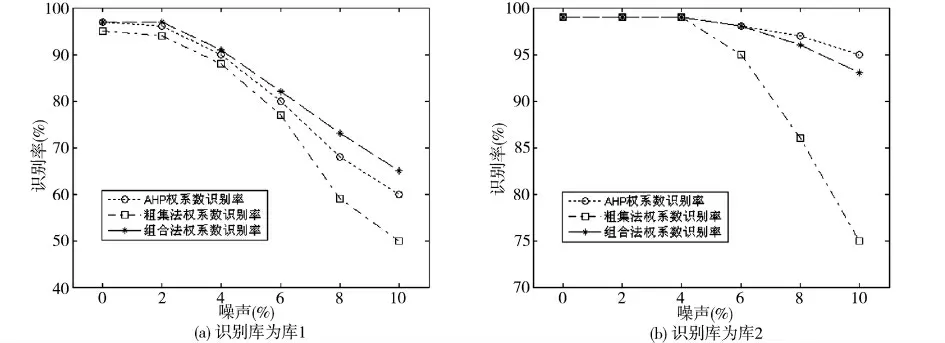
图1 3 种赋权法所得权系数识别率比较

由仿真结果可知:层次-粗集组合赋权法不是将AHP和粗集法两种方法的权系数识别率进行简单的平均，而是充分利用了主客观赋权法各自的优点。当样本数据较少时，可弱化粗集法权系数不够准确的问题;当样本数据较多时，要比AHP 权系数更加客观化，在噪声增大时也更稳定。因此，在不能确定样本数据是否充足时，使用层次-粗集组合赋权法是不错的选择。

6 结束语

雷达辐射源识别是个复杂的过程，影响识别率的因素很多。本文研究了待匹配特征参数的权系数对于识别率的影响，讨论了层次分析法和粗糙集理论两种赋权方法。在此基础上提出了层次-粗集组合赋权法，并将其运用到雷达辐射源识别中。该方法充分挖掘了识别数据库本身的信息，也利用了专家的知识和经验，消除了冗余信息，对提高辐射源识别系统的识别率起到了积极的作用。

［1］许宏泉，刘庚.雷达辐射源识别技术综述［J］.舰船电子工程，2010，30(4）:25-27.

［2］周霖仪，刘志成，何佳洲.层次-熵值组合赋权法在雷达辐射源识别中的应用［J］.指挥控制与仿真，2009，31(6）:27-29.

［3］许树伯.层次分析法原理［M］.天津:天津大学出版社，2003.

［4］PAWLAK Z.Rough sets and intelligent data analysis［J］.Information Sciences，2002，147:1-12.

［5］苗夺谦，李道国.粗糙集理论、算法与应用［M］.北京:清华大学出版社，2008.

［6］郑学敏.一种基于粗糙集理论的多指标综合评价方法［J］.统计与决策，2010(5）:37-39.

［7］叶军，王磊.一种基于粗糙集和层次分析法的综合评价方法研究［J］.计算机应用研究，2010，27(7）:2486-2488.