基于贝叶斯判别法的超视距雷达探测距离预测方法＊

练学辉，王向敏，申宏亚，王玲玲＊

(1.海军驻南京地区雷达系统军事代表室，南京 210003;2.南京船舶雷达研究所，南京 210003)

1 引言

海上大气波导条件下电磁波存在超视距传播现象，有时候雷达的探测距离达到几百公里甚至上千公里。但是，当雷达探测设备在海上工作时所遇到的外界环境极其复杂，大气传播过程中的吸收、折射和多路径效应都会影响到海上超视距雷达探测设备的距离性能，再加上无法精确知道目标特性以及工作时电波传播的环境特性，而使其有效探测距离难以估算和预测。为准确预测雷达探测性能，通过提取不同距离处海杂波强度和海杂波延伸距离等信息，利用贝叶斯判别法预测超视距雷达探测距离等级。

2 杂波功率

根据雷达作用距离方程［1］，当电磁波在自由空间传播时雷达的作用距离(即雷达最大探测距离）与接收功率的关系为

式中，Pt为雷达发射机功率，G为雷达天线增益，λ为雷达工作波长，Smin为雷达灵敏度，σ为目标反射面积，Lw为传播损耗。

电磁波在大气波导内是以折射传播方式进行，波前在空间上不是球面，而是类似于圆柱面，此时雷达的作用距离与接收功率的关系由1/4 次方变为1/2 次方来决定。雷达最大探测距离方程为

式中h为大气波导的高度。雷达接收的来自海面杂波信号的功率可表示为

式中，Pt为雷达发射功率，G为天线增益，λ为雷达信号波长，R为距离，Lr为雷达综合损耗，σc为杂波散射截面。对于常规脉冲雷达，在波束入射余角θg较小时，杂波散射截面可表示为

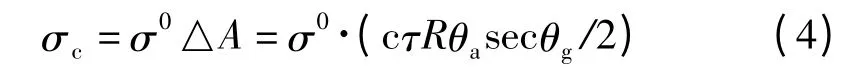
式中，σ0为海面的后向散射系数，△A为雷达分辨单元面积，c为光速，τ为脉冲宽度，θa为雷达天线方向波束宽度。

假设雷达工作和环境参数如表1，在不同波导高度情况下海杂波接收功率随着距离的变化趋势如图1。由此可见，如果大气波导连续出现，在大气波导范围内不考虑衰减的理想状态下，在相同距离处海杂波功率比无大气波导时明显增强。

《美国药学教育杂志》研究的对象涵盖范围全面，从教学管理者、教师以及在校学生拓展到毕业生、药师、学生家长甚至患者。应丰富我国高等药学教育的研究对象，全方面的探讨高等药学教育的现状以及发展趋势。

表1 雷达工作和环境参数

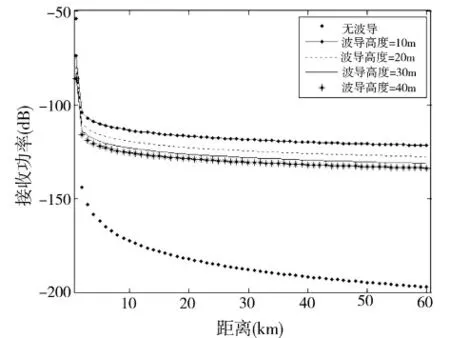
图1 在不同波导高度下海杂波随着距离变化趋势

3 超视距雷达探测距离预测

在不同的天气条件下，采用X波段多功能超视距探测设备进行数据采集，从雷达回波采集数据中得到高分辨力的雷达回波信号，研究各种海上气象环境下雷达回波的杂波特征，并对雷达回波进行分类。采取统计分析的方法，研究雷达回波强度与最远探测距离的关联性，建立了海用雷达探测效能预测模型。

3.1 数据采集

将X波段多功能超视距探测系统架设在南海某地海堤上，海拔15 m。7 月，雷达开始对海上非合作目标进行探测试验，每天早、中、晚开机，每次开机时间不超过30 min。雷达预热后，设置天线的转速为30°/s，环扫，观测整个海面的态势并跟踪海上目标，同时采集目标回波和杂波数据，记录跟踪稳定时最远目标的距离和此时天气情况。

3.2 雷达回波数据分析

在有大气波导和无大气波导两种情况下分别提取最远目标所在方位的10个主触发的数据求平均，得到海杂波的强度谱(如图2、3中下方的曲线），再根据具体海况仿真出无大气波导下海杂波功率随着距离的变化趋势(如图2、3中上方的线条）。通过实测海杂波强度与无大气波导下海杂波功率的对比，可见在无大气波导情况下实测海杂波强度与仿真的海杂波功率有较好的一致性(如图2）;在有大气波导情况下实测海杂波强度明显高于仿真的无大气波导海杂波功率(如图3），这与理论上有大气波导情况下电磁波的传播损耗较小相符合。

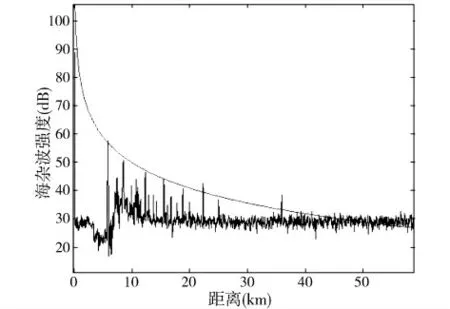
图2 无大气波导时海杂波的强度谱

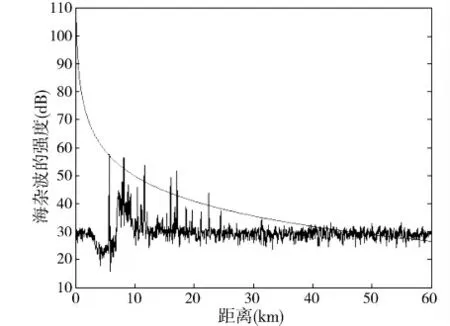
图3 有大气波导时海杂波的强度谱

(a）无大气波导

文件名:20070730122505～0.dat(天线正常转动，30 °/s）

数据说明:X波段雷达对海通道回波数据(波束中心方向仰角指向0°）

天线正常转动，海杂波抽取方位:115°

风向:顺风

最远目标:在30 km 以内

(b）有大气波导

文件名:20070727215119～0.dat(天线正常转动，30 °/s）

数据说明:X波段雷达对海通道回波数据(波束中心方向仰角指向0°）

天线正常转动，海杂波抽取方位:121°

海况:1

风向:顺风

最远目标:距离181 km，方位121°

3.3 数据提取与定性分析

3.3.1 数据提取

(1）海杂波强度数据

首先求最远探测目标方位上10个主触发的平均值，再以1.2 km为一个距离格，在平均值中找出每个格子内海杂波强度的最大值。如果该范围内有运动或固定目标，则缩小方位大小或者删除该距离格。

(2）海杂波延伸距离

求出慢门限，统计每一个格子内的回波强度。如果该回波强度有70%超过该门限，且该距离格子之后的统计均小于70%，则认为此处就是海杂波的延伸距离。

(3）预测等级

由于雷达的探测距离与目标特性有关，在该特性未知的条件下，可以把雷达探测距离分为0、1、2、3、4、5 共6 级，分别对应落在视距、视距～80 km、80～120 km、120～180 km、180～240 km、240～300 km的探测距离范围。

3.3.2 定性分析

利用matlab2010中提供的NaiveBayes类，用NaiveBayes.fit方法根据训练样本创建一个朴素贝叶斯分类器对象nb，输入参数是64*51的训练样本观测值矩阵，它的每一行对应一个观测值，每一列对应一个变量。再利用对象的predict方法对待判样品进行分类。从南海数据中抽取64个样本，在海杂波延伸距离内计算出每个格子内海杂波强度与仿真杂波的增量;在海杂波延伸距离外，增量值设为0。

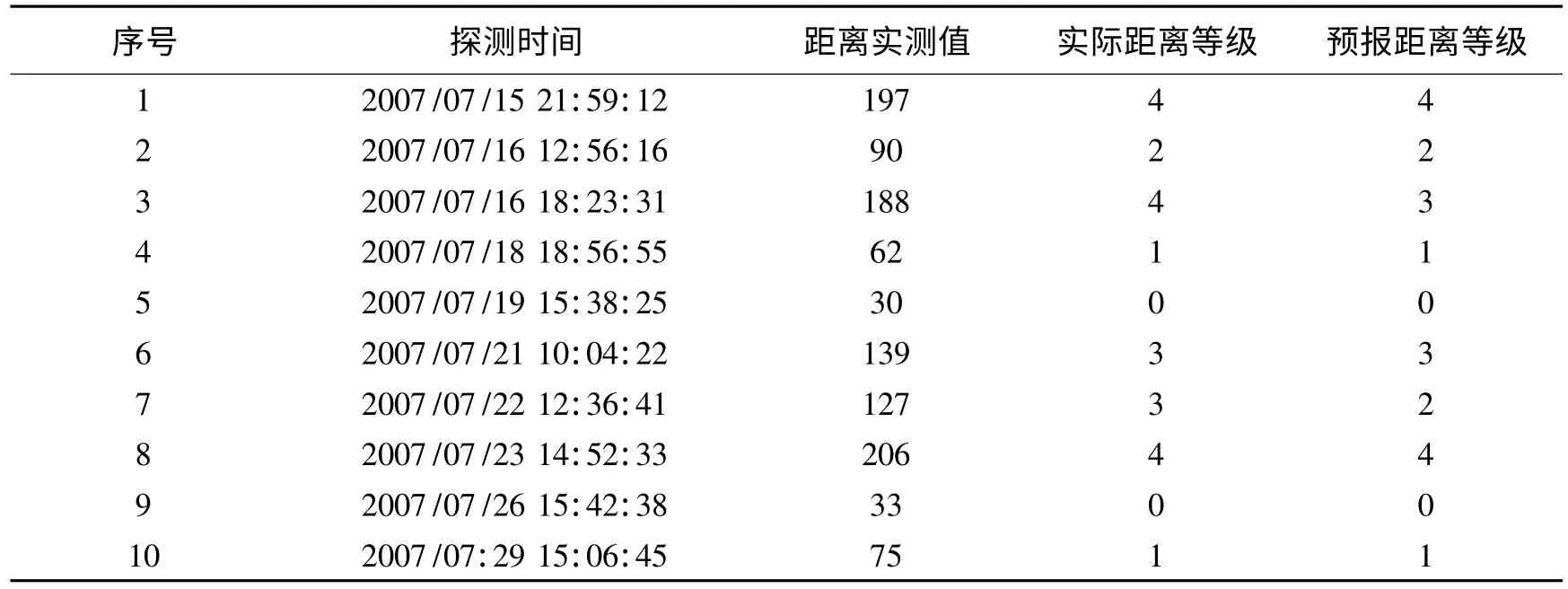
表2 独立样本的检验结果

4 结束语

由表2的初步分析结果可知总的预测准确率较高，但由于序号为3、7的样本处于距离划分等级的边界，故出现距离等级误判，后续研究重点将进一步积累有关超视距雷达探测数据及相应气象条件数据，增加模型的统计样本数，以便能够掌握在特定海域各种气象条件下超视距雷达探测距离的变化规律，提高预测准确率。

［1］张文祥.海面超视距效应研究［C］.第二届军事海洋战略与发展论坛论文集，2005:645.

［2］陈鲍，陈云秋，陈世友.海杂波建模与仿真［J］.舰船电子工程，2009，2(4）:95-98.

［3］谢中华.Matlab 统计分析与应用［M］.北京航空航天大学出版社，2010.