基于柔度曲率矩阵的加筋板结构损伤识别方法

马 骏，陈 立，赵德有

（1大连理工大学 船舶工程学院，辽宁 大连 116024；2大连船舶重工集团设计研究所有限公司，辽宁大连 116021）

基于柔度曲率矩阵的加筋板结构损伤识别方法

马 骏1，陈 立2，赵德有1

（1大连理工大学 船舶工程学院，辽宁 大连 116024；2大连船舶重工集团设计研究所有限公司，辽宁大连 116021）

为了对船舶工程中典型结构即加筋板结构的损伤部位进行准确的损伤识别分析，文章提出了一种基于柔度曲率矩阵的损伤识别方法并进行了仿真分析。首先对加筋板结构进行单元划分，以结构响应通过矩阵的列最大值来建立节点柔度矩阵，并通过二阶微分对柔度值的变化进行放大进而得到柔度曲率矩阵，最后通过柔度曲率矩阵图或者柔度曲率矩阵的行（列）曲率图来判断损伤位置。算例分析表明，该方法损伤定位准确并且具有较高的灵敏度，避免了使用原未损结构的模态参数，只需损伤结构的一阶或者前几阶模态信息就可以有效地进行损伤识别分析。通过大量模拟，给出了加筋板结构损伤的判别图。

加筋板；损伤识别；柔度矩阵；柔度曲率

1 引 言

结构的损伤可间接地通过模态参数的改变来判断，这一现象被广泛地应用到结构工程中来进行结构的损伤检测或者健康监测，所以寻求一种对于结构损伤非常敏感的模态参数至关重要。近年来，众多学者就此问题提出了很多无损检测方法。Cawley等[1]首先基于有限元以及固有频率的变化来判断损伤位置，该方法只能检测单一损伤的结构；Williams等[2]同样通过固有频率的变化对多损伤的结构进行了损伤识别分析，该方法假设一种频率的变化模式对应一种损伤模式，再通过比较和分析完好结构的固有频率与损伤结构的固有频率来进一步确定损伤位置。此后，学者们提出了基于模态柔度的损伤检测的理论与方法。对于结构中的局部损伤，Raghavendrachar和Aktan[3]证明了模态柔度要比固有频率或结构刚度更加敏感；在梁结构的损伤检测中，Pandey等[4]论证了模态柔度是一个很好的损伤指标；Lu等[5]发现柔度曲率要比模态柔度更加敏感并基于柔度曲率进行了多损伤结构的识别分析；曹晖等[6]以模态柔度曲率差为损伤指标对简支梁与连续梁结构进行了损伤识别；李永梅等[7-8]以柔度矩阵的主对角元素为损伤指标取得了很好的结果。以上基于柔度的方法和理论都是在一维空间下，所以只能应用到梁结构或桁架结构中，而基于模态柔度的二维空间理论在近几年才有了研究成果。Battipede等[9]提出对于板结构，柔度模态振型是一种有效的损伤指标；Wu等[10]通过Chebyshev多项式来模拟板结构表面曲率变化，得出模态曲率可以有效地进行损伤识别。然而以上方法都需要比较原始未损伤结构的模态参数与损伤后结构的模态参数来判断损伤位置，由于原始结构的模态参数很难获得，所以不需要原结构模态参数的方法技术就显得格外重要。

本文以柔度曲率矩阵为识别参数，对加筋板结构进行了损伤识别分析。柔度曲率在损伤位置和附近位置都会有较大的变化，通过柔度曲率矩阵图或者矩阵的行（列）曲率图来判断损伤位置。该方法不需要比较损伤前后结构的柔度曲率，直接利用损伤结构的柔度曲率来进行损伤识别而且只需要一阶或前几阶模态信息。

2 基本原理

由结构模态数据，可以容易得到结构的刚度矩阵和柔度矩阵：

式中，mi为模态质量，ωi为损伤结构的第i阶固有频率，φi为相应的位移或转角向量，r为模态阶数，M为质量矩阵。

假设在损伤处的质量不变，那么第i阶模态质量为：

式中，ρ为结构材料密度，h为结构的厚度，φi为模态振型，S为结构的面积。

将加筋板结构按照图1所示进行单元划分。

图1中X、Y、Z分别为X轴方向、Y轴方向和Z轴方向；w、η分别为Z轴方向与Y轴方向位移；θX、θY、θZ分别为绕X轴转角、绕Y轴转角和绕Z轴转角。在板中的节点只考虑由图1中（b）所示的自由度，而在筋中的节点只考虑由图1中（c）所示的自由度。

加筋板结构按照以上单元可以划分成（a-1）×（b-1）个单元。假设位移或转角向量可以表示为：

其中 n=a×b。

图1 加筋板结构的单元自由度Fig.1 Degree of freedom of the stiffened panel

那么由（2）式可以得到柔度矩阵K-1：

假设Ck为矩阵K-1第k列最大值：

那么可以得到过度矩阵Ft：

则由过度矩阵Ft可以得到节点柔度矩阵Fn：

对于板结构，每个节点考虑Z轴方向位移、X轴方向转角和Y轴方向转角的柔度值，则每组横、纵向n个节点的n个柔度是位置坐标的函数，在结构损伤点附近，柔度值相对来说将有改变，这个改变通过二阶导数的作用，将会变得更为明显。

横向柔度曲率矩阵Fch为：

纵向柔度曲率矩阵Fcv为：

式中)为（b-1）阶单位阵，Eb×b为 b 阶单位阵，S为单元面积。

对于加筋板的损伤识别，可先对加筋板中板结构进行识别，然后对筋进行损伤识别。由损伤结构的柔度曲率矩阵绘出图像，或者由矩阵的行或列曲率图，通过比较就能直接得出损伤位置。

3 算例分析

由于加筋板结构中损伤可以出现在板中或筋中，或者两者同时出现损伤，这里只就几个典型的例子加以讨论。

3.1 加筋板结构的损伤出现集合A中

考虑如图2所示的加筋板结构，具体参数如下所示：板结构的长为4.0 m，宽为1.6 m；加强筋位于板的纵向中面，高度为0.2 m；板与加强筋的厚度都为0.01 m。材料的弹性模量E=206 GPa，泊松比μ=0.3，密度为ρ=7 850 kg/m3；黑色单元为模拟损伤位置，弹性模量E=103 GPa，即用弹性模量的减少来模拟损伤，泊松比μ=0.3，密度为ρ=7 850 kg/m3。单元网格大小为0.1 m×0.1 m。板结构边界条件为四边固支，加强筋为两端固支，另外一边为自由边界。

在有限元处理中，相对应图中的节点编号用矩阵A1表示，相对应图中的单元编号用矩阵A2表示:

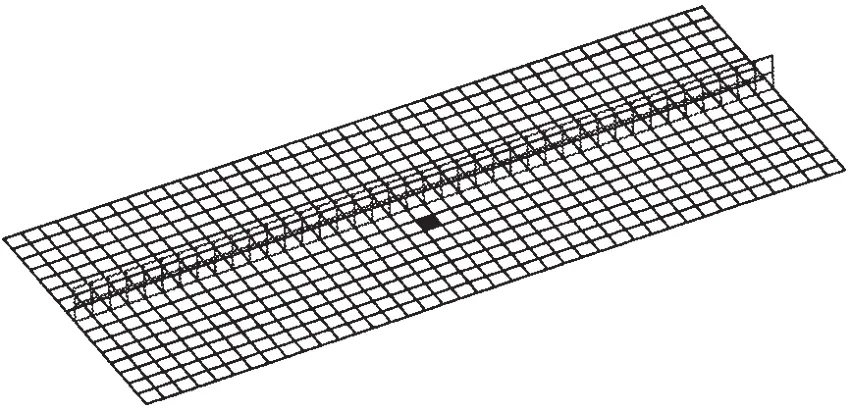
图2 损伤出现集合A中的加筋板结构Fig.2 Stiffened panel with set‘A’damage

在以上两个矩阵中最后两行分别为加强筋节点编号与单元编号。相对应有限元的损伤的节点编号为266、267、308、307，单元编号为 260。

通过仿真模拟，结构的固有频率 ωi（i=1,2,…,6）与结构的位移或转角向量 φi（i=1,2,…,6）都可以获得，mi可通过计算得到。以下算例除了模拟损伤的位置不同，其余部分与以上相同。

3.1.1 加筋板中板结构柔度曲率的表征

考虑位移向量，由（7）式得到前1阶至前6阶关于位移的节点柔度矩阵，如图3所示。

由图3可以看出，节点柔度矩阵无法用来判断损伤位置。由（8）式得到前1阶到前6阶的位移横向柔度曲率矩阵图，如图4所示。

由图4可以看出，从前1阶到前6阶的横向柔度曲率矩阵图都可判断出有损伤出现，即在损伤单元附近柔度曲率有了较大的变化。对于损伤识别来说，所需模态阶数越少越好，且在低阶模态下，柔度曲率矩阵的行或列曲率图应该是连续的，一旦出现跳跃点，那么就可认为在此处有损伤出现，则选择图4中的子图‘a’来判断损伤位置。

图3 集合A前1阶至前6阶节点位移柔度矩阵图Fig.3 Flexibility damage index matrix about displacement of set‘A’ with r=1,…,6

图4 集合A前1阶至前6阶的位移横向曲率图Fig.4 Transverse direction flexibility curvature matrix of displacement of set‘A’ with r=1,…,6

下面给出子图‘a’的矩阵的行曲率图来进一步判断损伤位置，如图5所示。

由图5看出在损伤单元的节点及其附近曲率值发生变化，可以判断编号为260的单元是损伤位置。在图6中我们同时给出了非加筋板结构与加筋板结构关于位移的横向柔度曲率矩阵的第21行曲率图。由图6可以看出，正是由于有筋的存在，加筋板的行曲率图中部才会出现极值。

图5 集合A前1阶第20行至23行的位移横向曲率图Fig.5 The 20th to 23th row in transverse direction flexibility curvature matrix about displacement with r=1

图6 加筋板第21行与非加筋板第21行的位移横向曲率图Fig.6 Comparing the 21th row in transverse direction flexibility curvature matrix about displacement between stiffened and plate

由（9）式得到前1阶到前6阶的纵向柔度曲率矩阵图，如图7所示。由图7可以看出，从前1阶到前6阶的纵向柔度曲率矩阵图都可判断出有损伤出现，即在损伤单元附近柔度曲率有了较大的变化，同样选择图7中的子图‘a’来判断损伤位置。下面给出子图‘a’的矩阵的行曲率图来精确地判断损伤位置，如图8所示。

由图8看出在损伤单元的节点及其附近曲率值发生较大的变化，可以判断编号为260的单元是损伤位置。

下面给出横向柔度矩阵中筋所在列及两侧各一列的图像与纵向柔度曲率矩阵中筋所在行的图像，如图 9、10 所示。

由图9可以看出第7列与筋所在列的曲率值在节点20、21有所变化，说明如果集合A中损伤靠近筋板交界，就会影响到横向柔度曲率矩阵中筋所在列的柔度曲率值。而图10中筋所在行的柔度曲率值没有变化，说明集合A中损伤不影响板的纵向柔度曲率矩阵中筋所在行的柔度曲率值。

图7 集合A前1阶至前6阶的位移纵向曲率图Fig.7 Lengthways direction flexibility curvature matrix about displacement of set‘A’ with r=1,…,6

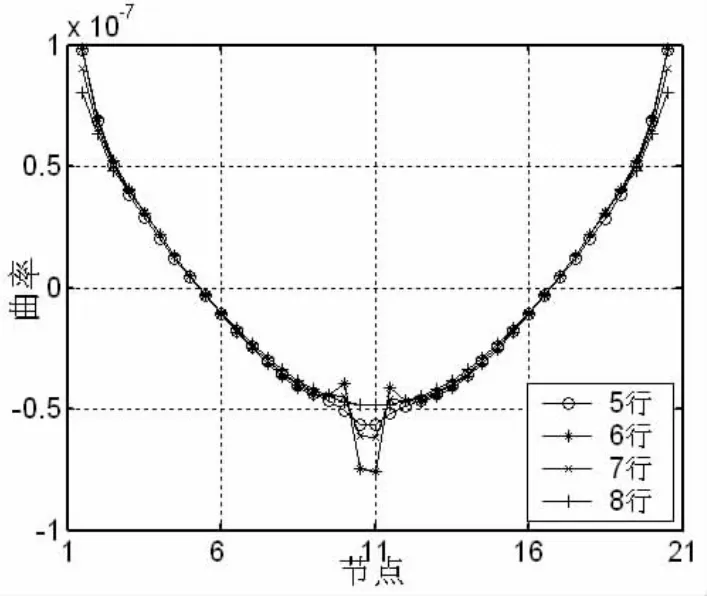
图8 集合A前1阶第5行至8行的纵向位移曲率图Fig.8 The 5th to 8th row in lengthways direction flexibility curvature matrix about displacement with r=1

图9 集合A横向柔度矩阵中筋所在列及两侧各一列图像Fig.9 The column of web and the column on each side of the web in transverse direction flexibility curvature matrix about displacement

图10 纵向柔度曲率矩阵中筋所在行图像Fig.10 The row of web in lengthways direction flexibility curvature matrix about displacement

关于位移向量，由以上结论可以看出其纵向曲率矩阵图要比横向曲率图在损伤部位的变化要更加明显，分析得出，主要是由加筋板结构的边长比所致，同时筋也起到减少弯曲的作用。关于转角向量，损伤识别的过程和结论与关于位移向量中的讨论一致，只是其效果要较位移向量更好，在此算例与以后算例中都不再重复。

3.1.2 加筋板中筋结构柔度曲率的表征

与板结构一样，由筋的节点柔度矩阵同样不能进行损伤识别。由于筋的长宽比很大，这里只考虑其纵向曲率，那么由（8）式得到前1阶到前6阶的位移纵向柔度曲率矩阵图，如图11所示。

图11 集合A前1阶至前6阶的位移纵向曲率图 Fig.11 Lengthways direction flexibility curvature matrix about displacement of web of single damage stiff- ened panel with r=1,…,6

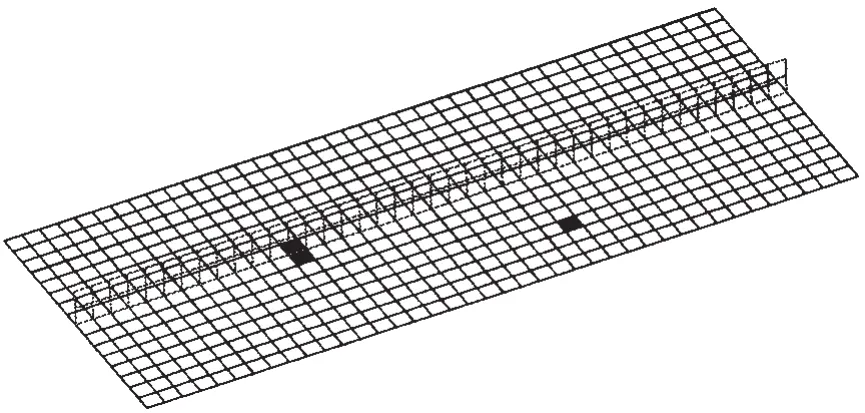
图12 损伤出现在集合A+B中的加筋板结构Fig.12 Stiffened panel which the damage is included by set A+B

在模型里，筋上没有模拟损伤，但是由图11可以看到，前1阶到前6阶的纵向柔度曲率矩阵图的中部都有较大的突起存在。经过大量模拟得出，该突起是由板结构中的损伤所造成的，如果筋中有损伤出现，应该选择图6中的子图‘b’来判断损伤位置。

由以上结论可知，加筋板中板的损伤识别只需用到一阶模态信息，而筋的损伤识别只需用到前二阶模态信息。由于加筋板复杂且板中损伤会影响到筋的柔度曲率，下面将讨论一些多损伤的情况。

3.2 加筋板结构的损伤出现集合A+B中

考虑如图12所示的加筋板结构。

由（8）、（9）式分别得到板结构前1阶位移横向与纵向柔度曲率矩阵图，如图13、14所示。

由图13看出，损伤部位及附近的柔度曲率值都有较大的变化，所以该方法可以进行多损伤识别。由图14看出，可以判断集合A的损伤位置，而在集合B中，柔度曲率值发生变化的单元很多，不能判断损伤位置。

下面给出横向柔度矩阵中筋所在列及两侧各一列的图像与纵向柔度曲率矩阵中筋所在行的图像，如图15、16所示。

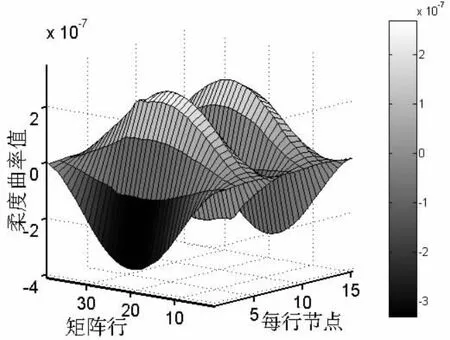
图13 集合A+B前1阶位移横向曲率图Fig.13 Transverse flexibility curvature about displacement with r=1 which the damage is included by set A+B

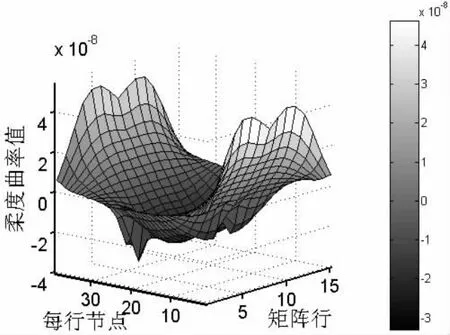
图14 集合A+B前1阶位移纵向曲率图Fig.14 Lengthways flexibility curvature about displacement with r=1 which the damage is included by set A+B

图15 集合A+B横向柔度矩阵中筋所在列及两侧各一列图Fig.15 The column of web and the columns on each side of the web in transverse flexibility curvature by set A+B

图16 集合A+B纵向柔度曲率矩阵中筋所在行图Fig.16 The row of web in lengthways flexibility curvature matrix about displacement by set A+B

由图15可以看出第7列至第9列的曲率值在节点20、21处有所变化，而且筋所在列的柔度曲率变化是外凸的，对比图4可以看作是由于损伤出现在筋板交界，筋的作用加强的结果。而图16中筋所在行的柔度曲率值没有变化，说明集合B中损伤同样不影响板的纵向柔度曲率矩阵中筋所在行的柔度曲率值。

由（9）式得到筋前1阶位移纵向柔度曲率矩阵图，如图17所示。由图17可以看出有2处突起，同样得出突起是由板中的损伤所造成的，而且损伤位置越靠近板与筋的交界，柔度曲率值的变化越大。

3.3 加筋板结构的损伤出现在集合C+D中

考虑如图18所示的加筋板结构。

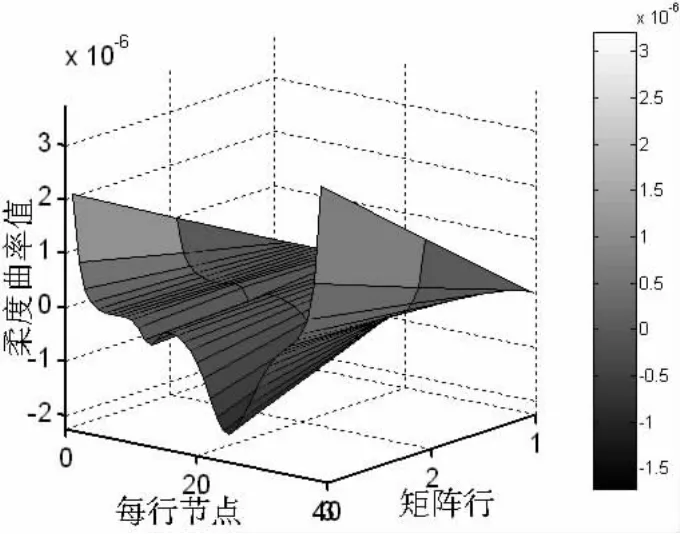
图17 集合A+B前1阶位移纵向曲率图Fig.17 Lengthways flexibility curvature about displacement of web with r=1 by set A+B

图18 损伤出现在集合C+D中的加筋板结构Fig.18 Stiffened panel which the damage is included by set A+B

由（8）、（9）式分别得到板结构前1阶位移横向与纵向柔度曲率矩阵图，如图19、20所示。同时给出横向柔度矩阵中筋所在列及两侧各一列的图像与纵向柔度曲率矩阵中筋所在行的图像，如图21、22所示。

由图19、21看出，筋的损伤同样会影响到板的柔度曲率的变化，影响位置都集中在板筋交界处，且筋所在列的柔度曲率变化是下凹的，集合C中的损伤比集合D中的损伤在交界处引起的曲率变化更明显，同时筋两侧的曲率值并没有变化。可以看作是由于损伤出现在筋板交界，筋的作用减弱的结果。由图15、21可以看出，就单损伤而言，如果横向柔度曲率矩阵中筋所在列上凸，则集合B中有损伤出现；如果所在列下凹，则集合D中有损伤出现。

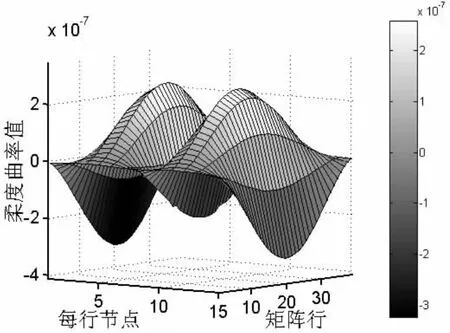
图19 集合C+D前1阶位移横向曲率图Fig.19 Transverse flexibility curvature about displacement of plate with r=1 by set C+D

图20 集合C+D前1阶位移纵向曲率图Fig.20 Lengthways flexibility curvature about displacement of plate with r=1 by set C+D

图21 集合C+D横向柔度矩阵中筋所在列及两侧各一列图 Fig.21 The column of web and the columns on each side of the web in transverse flexibility curvature about displacement by set C+D

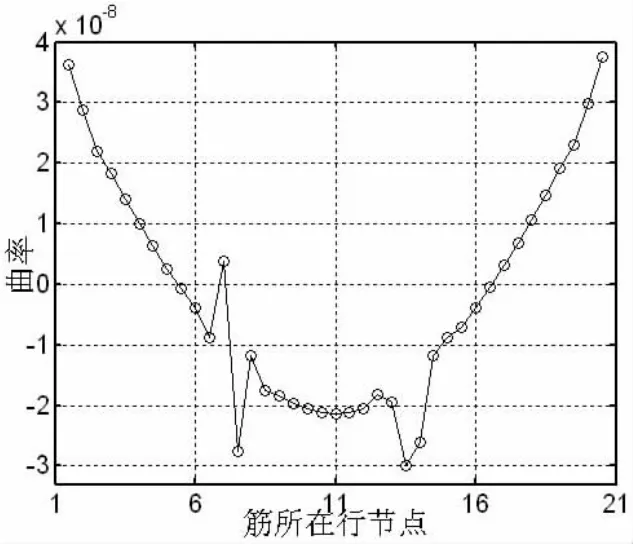
图22集合C+D纵向柔度曲率矩阵中筋所在行图Fig.22 The row of web in lengthways flexibility curvature about displacement by set C+D

由图22看出，集合D中的损伤会使筋的柔度曲率出现2个极值，而集合C中的损伤使筋的柔度曲率只出现1个极值，即2个极值对应的是集合D中有损伤存在，1个极值对应的是集合C中有损伤存在，那么纵向柔度曲率矩阵中筋所在行的图像可以用来判断筋中是否有损伤存在且损伤所属集合。则由（9）式得到筋前2阶位移纵向柔度曲率矩阵图来判断筋的损伤位置，如图23所示。

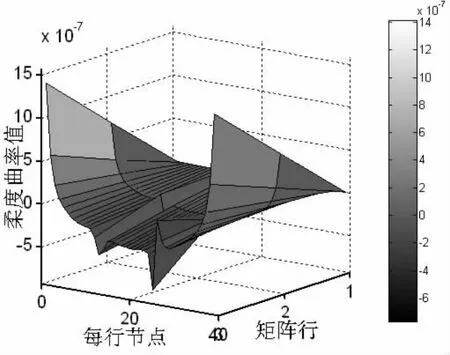
图23 集合C+D前1阶位移纵向曲率图Fig.23 Lengthways flexibility curvature about displacement of web with r=1 by set C+D

图24 损伤出现在集合E中的加筋板结构Fig.24 Stiffened panel which the damage is included by set E

由图23可以判断出集合C中的损伤位置，而对于集合D中的损伤，只能判断损伤区域。

由于板的损伤会影响到筋的曲率变化，同时筋的损伤也会影响到板的曲率变化，下面的算例将讨论同列单元都发生损伤的情况。

3.4 加筋板结构的损伤出现在集合E中

考虑如图24所示的加筋板结构。

由（8）式得到板结构前1阶位移横向柔度曲率矩阵图，同时给出横向柔度矩阵中筋所在列及两侧各一列的图像，如图25、26所示。

由图25、26看出，损伤部位及附近的柔度曲率值都有较大的变化，筋两侧列曲率值也有变化，那么可以判断板的损伤位置。

图25 集合E前1阶位移横向曲率图Fig.25 Transverse flexibility curvature about displacement of plate with r=1 by set E

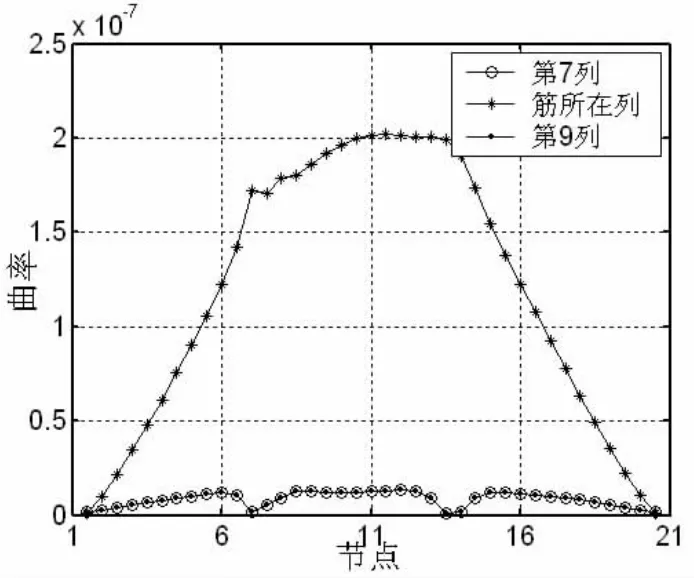
图26 横向柔度矩阵中筋所在列及两侧各一列图Fig.26 The column of web and the columns on each side of the web in transverse flexibility curvature by set E

由（9）式得到的板结构前1阶位移纵向柔度曲率矩阵图与图20基本相同，说明无论集合A+B中是否有损伤出现，只要集合C+D中有损伤出现，纵向柔度曲率矩阵中筋所在行的图像一定会有1至2个极值出现，结论与算例3.3中的结论相同。那么由（9）式得到筋前2阶位移纵向柔度曲率矩阵图与图23基本相同，所得到的结论也与算例3.3中结论相同，可以判断筋上的损伤位置和损伤区域。

4 结 论

本文以柔度曲率为识别参数，针对加筋板结构进行了损伤仿真分析。提出一种基于柔度曲率的加筋板结构分析方法和判断准则，即对板的横向、纵向分别进行柔度曲率分析，最后可以得到损伤位置。不需要原始模态数据就可以对已损伤板进行损伤识别分析。只需要前一阶固有频率和相应的位移向量就可以判断损伤位置，而且可以得到很好的结果。由前一阶固有频率和相应的转角所得到的柔度曲率矩阵所绘制的图同样可以精确判断出损伤位置，由于转角变化要比位移变化更大，所以其效果较位移向量所得到的结果更为明显。无论是位移向量还是转角向量，纵向曲率矩阵判断损伤的效果都要好于横向曲率矩阵，这是由于加筋板的长宽比与加强筋共同作用的结果。

图27 至多出现2处损伤的加筋板结构损伤判别图Fig.27 Judging figure of stiffened panel which has 1 or 2 damages

在加筋板中，板中的损伤会影响到筋的曲率值的变化，同样筋中的也会影响到板的曲率值的变化，且损伤越靠近板与筋的交界处，曲率值受到影响所产生的变化越大，所以加筋板损伤识别的难点为筋与板的交界处。就单损伤而言，如果横向柔度曲率矩阵中筋所在列图外凸，则集合B中有损伤出现，如果所在列图内凹，则集合C+D中有损伤出现；如果纵向柔度曲率矩阵中筋所在行图出现极值，那么集合C+D中一定有损伤出现，且1个极值对应的是集合C中有损伤出现，2个极值对应的是集合D中有损伤出现。说明横向柔度曲率矩阵中筋所在列图与纵向柔度曲率矩阵中筋所在行图在加筋板结构损伤识别中起着重要的作用。下面对至多出现2处损伤的加筋板结构，给出损伤的判别图，如图27所示。其中：（1）板结构的横向曲率矩阵图像，（2）板结构的纵向曲率矩阵图像，（3）板结构纵向曲率矩阵筋所在行图像，（4）板结构横向曲率矩阵筋所在列图像，（5）板结构横向曲率矩阵筋两侧各一列图像；集合A、B、C、D与以上介绍的相同，集合F为板结构中没有损伤出现，各集合的损伤位置的判断已在算例中给出。如果出现3处或3处以上损伤，其损伤情况可以分解为上图所示情况来判断。

[1]Cawley P,Adams R D.The location of defects in structures from measurements of natural frequencies[J].Journal of Strain Anal,1979,14:49-57.

[2]Williams E J,Messina A.Applications of the multiple damage location assurance criterion[J].Key Engineering Materials,1999,167-168:164-256.

[3]Rahavendrachar M,Aktan A.Flexibility by multireference impact testing for bridge diagnostics[J].Journal of Structural Engineering,1992,118(8):2186-2203.

[4]Pandey A K,Biswas M,Samman M M.Damage detection from changes in curvature mode shapes[J].Journal of Sound and Vibration,1991,145(2):321-332.

[5]Lu Q,Ren G,Zhao Y.Multiple damage location with flexibility curvature and relative frequency change for beam structures[J].Journal of Sound and Vibration,2002,253:1101-1114.

[6]曹 晖,Michael I F.基于模态柔度曲率的损伤检测方法[J].工程力学,2006,23(4):33-38.

[7]李永梅,周锡元,高向宇等.柔度曲率法对梁结构的损伤诊断[J].北京工业大学学报,2008,34(11):1173-1178.

[8]李永梅,周锡元,高向宇.基于柔度差曲率矩阵的结构损伤识别方法[J].工程力学,2009,26(2):118-195.

[9]Battipede M,Ruotola R,Surace C.Damage detection of plate-like structures[J].Damage Assessment of Structures Key Engineering Materials,2001,204(2):27-34.

[10]Wu D,Law S S.Damage localization in plate structures from uniform load surface curvature[J].Journal of Sound and Vibration,2004,267(1-2):227-244.

Damage detection in stiffened panel based on flexibility curvature matrix

MA Jun1,CHEN Li2,ZHAO De-you1
(1 Department of Naval Architecture,Dalian University of Technology,Dalian 116024,China；2 Dalian Shipbuilding Industry Engineering and Research Institute Co.,Ltd,Dalian 116021,China)

To detect and analyse the damage part of stiffened panel of the representative structure in ship engineering,a method,which is based on curvature flexibility matrix for the numerical simulation is presented.Instead of directly comparing the curvatures before and after damage,the method here uses modal parameters only in the damaged structure to detect the damage and consists of four steps:First,the stiffened panel is meshed into square elements.Second,the node flexibility matrix can be built with regard to structure response using absolute maximum in each column.Third,the curvature flexibility matrix is obtained in amplifying the variation of flexibility through second order differential coefficient.And finally,the damage location can be detected by the figure of flexibility curvature matrix or the figure of flexibility of array or column in the flexibility curvature matrix.The numerical analysis results indicate that this method is effective,useful and needs the lower mode data even the first mode data of the damaged structure.The detecting chart of damage detection in stiffened panel is obtained by lots of simulations.

stiffened panel;damage detection;flexibility matrix;flexibility curvature

U661.44

A

1007-7294（2011）08-0881-11

2011-01-06

马 骏（1963-），男，大连理工大学船舶工程学院副教授，E-mail:junma@dlut.edu.cn；陈 立（1979-），男，博士生。