AUV水下回收过程中的操纵性仿真研究
杜晓旭,宋保维,潘 光
(西北工业大学 航海学院,西安 710072)
AUV水下回收过程中的操纵性仿真研究
杜晓旭,宋保维,潘 光
(西北工业大学 航海学院,西安 710072)
在建立自主水下航行器(简称AUV)六自由度运动模型的基础上,基于势流理论建立了潜艇运动扰动流场对AUV扰动力的计算模型,并对回转体AUV在回收时靠近潜艇过程中的操纵性进行了仿真,仿真结果显示,AUV在靠近潜艇的过程中,潜艇扰动流场对AUV深度和侧向位移有较大的影响,而对姿态角的影响较小,因此,回转体AUV可以稳定地完成水下的回收运动。
自主水下航行器;潜艇运动扰动流场;回收
1 引 言
目前自主水下航行器(Autonomous Underwater Vehicle,简称AUV)在军事海洋技术、海洋科学技术考察、海底勘探、管路检修、海底打捞、油田勘探等多个领域具有广泛的应用。AUV通常要自带能源在水下工作,工作时间和航行距离都有限制,这就需要回收以补充能量、读取信息和维护部件。传统的AUV回收方式是,在AUV作业完成后上浮到水面,通过母船、中继站等其他辅助设备进行水面起吊回收。而当潜艇携带AUV用于水下目标探测、信息搜索、运载物品或者AUV为潜艇提供预警检测时,AUV完成使命后需要及时回收到潜艇以提取资料,由于潜艇活动范围的隐蔽性及安全性需要,AUV必须在水下完成回收[1]。这种回收方式的优点是受时间和空间的约束小,增加了AUV回收的隐蔽性,但是回收过程中AUV受到潜艇扰动流场的作用,对AUV的操纵性提出了更高的要求。因此,本文研究的目的就是对回转体型AUV回收过程中的操纵性进行仿真,对回转体型AUV能否在水下稳定地完成回收提供有意义的参考。
2 AUV六自由度操纵性方程
2.1 坐标系与运动参数的选择
本文中的坐标系选取地面坐标系、AUV体坐标系和潜艇体坐标系,分别记作SE(O ,x0,y0,z0)、SB(B, x ,y,z)和Sq(Bq, xq,yq,zq),如图1所示。
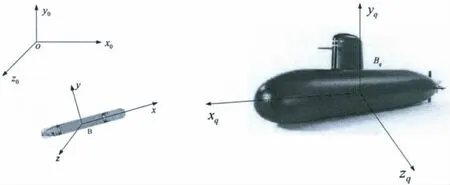
图1 AUV坐标系Fig.1 Coordinate and frame definitions of AUV
2.2 动力学方程

根据动量和动量矩方程,AUV的动力学方程可以写为[2-3]方程右端的f是指AUV受到的各种力,包括:理想流体惯性力、负浮力、粘性阻力、控制力和潜艇运动扰动流场对AUV的扰动力等。其中,理想流体惯性力、负浮力、粘性阻力和控制力等采用常规的方法计算,详见文献[2-3]。
2.3 运动学方程[3,5]
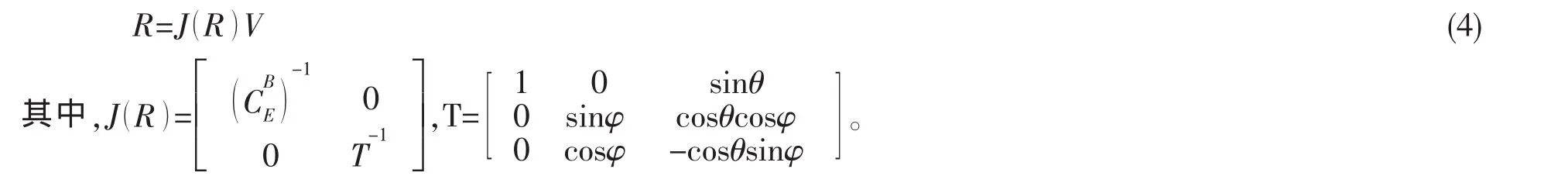
在由(1)式和(4)式组成的方程组中,共含有 vx、vy、vz、ωx、ωy、ωz、θ、ψ、φ、x0、y0、z0十二个未知数,在初始条件及控制规律已知的情况下封闭可解。
2.4 动力定位控制力
由于在微速状态下AUV的舵控制失效,因此在回收过程中AUV的控制力靠动力定位系统提供,也就是由主推进器和4个辅助推进器控制AUV的运动。当AUV由动力定位系统控制时,控制力由以下模型确定。假设AUV有n个推力装置,推力矩阵为[4]

其中Ti(i= 1 ,2,L,n )为第i个推力装置的推力。
假设由T产生的推力矢量U为[4-5]

式中L为推力映象矩阵,将T从推力空间映射到推力矢量空间,其形式为

其中Lji(j=1,2,L,6;i=1,2,L,n )为第i个推力对第j个自由度的影响系数。根据推力装置安装的位置以及自由度控制的需要,Lji一般是固定的,即L为常量矩阵。
从所需要的推力矢量U也可以通过反映象运算

得到推力矩阵T,即得到了每一个推力装置所需的推力。这里L*为伪逆矩阵,由下式确定

本文所研究AUV动力定位系统的推进器数量及其在AUV上的布置如图2所示。推进器1产生的推力沿Bx方向,推进器2、3产生的推力沿By方向,推进器4、5产生的推力沿Bz方向。具体到本AUV,(6)式中的T,L,U 有具体的形式,详见文献[4]。
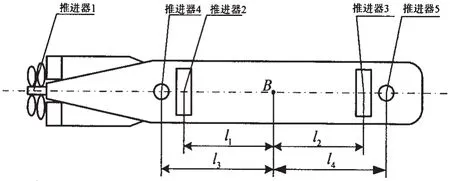
图2 推进器在AUV上的布置Fig.2 Thrusters’collocation on the AUV
3 潜艇运动扰动流场对AUV的扰动力
3.1 基本假设
AUV所受到的流体动力按力的成因分,由两部分组成,一部分是势流力Fp,另一部分是粘性力Fv。潜艇运动扰动流场对AUV的扰动力主要与势流力有关。因此,扰动力可以用AUV在扰动流场中运动时的势流力Fp1减去AUV在静水中运动时的势流力Fp2得到,即[2]

3.2 潜艇运动形成的扰动流场
在坐标系Sq(Bq, xq,yq,zq)中,设潜艇运动形成的扰动流场速度势为Φs,根据势流理论有[2,6]

式中,Ps为潜艇表面上任意一点;nsp为潜艇表面上点Ps处的单位外法线矢量;vsp为潜艇在点Ps处的速度。
采用表面分布源汇方法求解上述扰动流场。假设在潜艇表面连续分布的源汇强度面密度为σ(Qs),由于源汇自动满足方程(11)及外场边界条件(12),因此只要使其满足物面边界条件(13)即可,可用下式表示

式中,Ωs为潜艇粘湿表面积;Qs为潜艇表面任意与Ps相异的点;rQP为点Qs至Ps的距离。
3.3 AUV表面速度分布
AUV表面的流体质点速度由两部分组成:一部分为由于AUV本身运动产生的速度vcc,另一部分是由于潜艇运动产生的速度vsc。设Ps和Pc分别为潜艇表面与AUV表面上的任意点,则点Pc处由于潜艇运动产生的速度vsc可用下式计算[2]

式中,rsc为点 Ps至点 Pc的距离,rsc为点 Ps至点 Pc的单位矢径。
求解vcc的方法与求解vsc类似。设AUV运动流场的速度势为Φc,则根据势流理论有[7]:

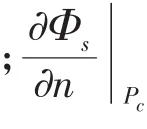
AUV表面用四边形单元近似,采用Hess-Smith数值方法求解(18)式时,将其改写为
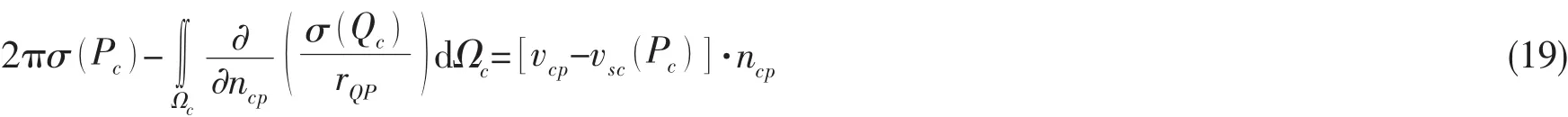
式中,Ωc为AUV粘湿表面积;Qc为AUV表面任意与Pc相异的点;rQP为点Qc至点Pc的距离。
在AUV表面源汇强度分布σ Qc()求出后,vcc可由下式计算:

其中,rQP为点Qc至点Pc的单位矢径。
最后,可以得到当AUV在潜艇扰动流场中运动时,AUV表面上任意一点处的流体速度vc1为

3.4 潜艇扰动流场对AUV的附加扰动力
动坐标系中的拉格朗日积分为[2]

式中,Φ为流场速度势;ve为动坐标系的牵连速度;v为流场速度;p为流场中的压力;f()t为时间常数。把(22)式应用于AUV在潜艇扰动流场中运动时的表面压力分布计算,有

则(22)式便可改写为


式中,vc0为AUV体坐标系原点的速度。
设表面上第j个单元上的压力系数为Cp1j,则受到的总的流体动力Fp1与力矩Mp1为[2]:

式中,Ωj为AUV表面第j个单元的面积;nj为AUV表面第j个单元的单位外法线矢量;rj为AUV表面第j个单元形心处的矢径;Nc为AUV表面划分的单元总数。
设AUV在静水中运动时的扰动速度势为Φc2,根据势流理论有

设AUV在静水中运动时,表面上第j个单元上的压力系数为Cp2j,则受到的总的流体动力Fp2与力矩 Mp2为[2]:


潜艇扰动流场对产生的附加扰动力ΔFp与力矩ΔMp为在潜艇扰动流场中运动时的流体动力Fp1与力矩Mp1和AUV在静水中运动时的流体动力Fp2与力矩Mp2之差,即

本文对AUV靠近潜艇过程中受到的附加扰动力进行了计算,计算结果见表1。

表1 AUV靠近潜艇过程中受到的附加扰动力Tab.1 Disturbed force of AUV when moving to submarine
4 仿真实例
本文对某低速回转体型AUV回收过程中的操纵性进行了仿真。仿真过程为,AUV在动力定位系统作用下,以1m/s的初速度,在水下10m深度,从离艇16m的距离开始靠近潜艇,直到AUV浮心离艇距离为3.9m时结束(这时AUV前端离艇约0.5m)。图3~4给出了AUV在靠近潜艇过程中深度和侧向位移受潜艇扰动流场的影响,图5~6给出了AUV在靠近潜艇过程中姿态角受潜艇扰动流场的影响。

图3 深度在靠近艇过程中的变化曲线Fig.3 Depth curve when moving to submarine
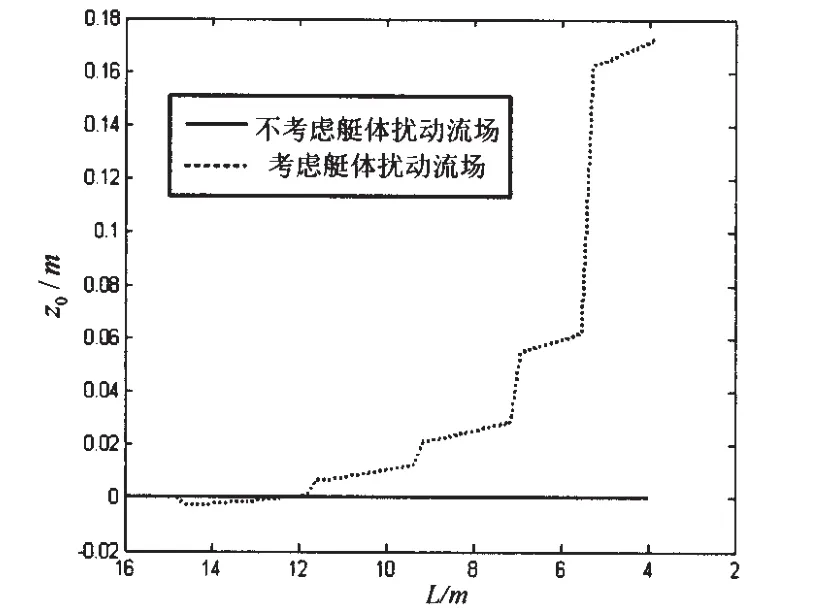
图4 侧向位移在靠近艇过程中的变化曲线Fig.4 Lateral displacement curve when moving to submarine
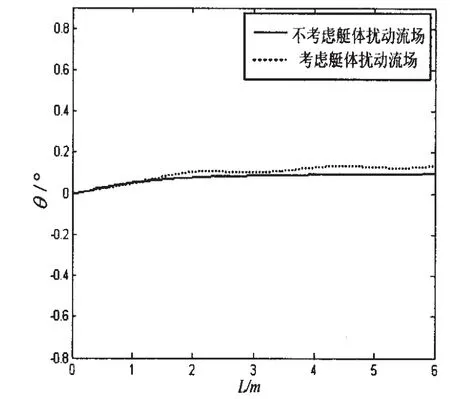
图5 俯仰角随时间的变化曲线Fig.5 Pitch angle curve
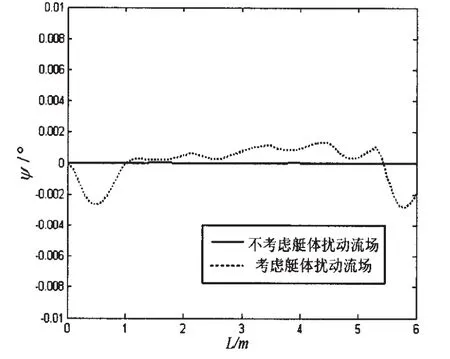
图6 偏航角随时间的变化曲线Fig.6 Yaw angle curve
由图3~4可以看出,回转体AUV在靠近潜艇的过程中,深度和侧向位移都受到潜艇扰动流场较大的影响,深度最大达到了0.327m的误差,侧向位移达到了0.173m的误差,这将对AUV的稳定安全回收产生一定的影响。从图5~6可以看出,回转体AUV在靠近潜艇的过程中,姿态角受到潜艇扰动流场的影响较小。
但由于回转体AUV在靠近潜艇的过程中,其最大误差没有超过AUV的最大直径,可以通过设计合适的回收装置完成安全回收。
5 结 语
本文在建立AUV六自由度运动模型的基础上,基于势流理论建立了潜艇运动扰动流场对AUV扰动力的计算模型,并对回转体AUV在回收时靠近潜艇过程中的操纵性进行了仿真,仿真结果显示,AUV在靠近潜艇的过程中,潜艇扰动流场对AUV深度和侧向位移有较大的影响,而对姿态角的影响较小,但通过设计合适的回收装置可以完成回转体AUV在水下的稳定安全回收。
[1]Yakimenko Oleg A,Horner Douglas P,Pratt Douglas G Jr.AUV rendezvous trajectories generation for underwater recov ery[C]//16th Mediterranean Conference on Control and Automation,June 25-27,2008.Ajaccio,France,2008:1192-1197.
[2]张宇文.鱼雷弹道与弹道设计[M].西安:西北工业大学出版社,1999.
Zhang Yuwen.Torpedo Trajectory and Trajectory Design[M].Xi’an:Northwestern Polytechnical University Press,1999.
[3]Smallwood David A,Whitcomb Louis L.Model-based dynamic positioning of underwater robotic vehicles:Theory and experiment[J].IEEE Journal of Oceanic Engineering,2004,29(1):169-185.
[4]杜晓旭,潘 光,宋保维,胡海豹,李家旺.远程AUV微速操纵性仿真研究[J].系统仿真学报,2007,19(3):470-473.
Du Xiaoxu,Pan Guang,Song Baowei,Hu Haibao,Li Jiawang.Simulation of long-distance AUV in low speed maneuvers[J].Journal of System Simulation,2007,19(3):470-473.
[5]宋保维,杜晓旭,胡海豹,王 鹏.近水面悬停远航程AUV受波浪的影响[J].西北工业大学学报,2007,25(4):482-485.
Song Baowei,Du Xiaoxu,Hu Haibao,Wang Peng.Effect of wave on AUV hovering near sea surface[J].Journal of Northwestern Poolytechnical University,2007,25(4):482-485.
[6]Denis Chapuis C F,Etat-Major de la Marine,Caroline Delthetl T H,Didier Leandri I C N,CTSN/DLSM.Determination and influence of the main parameters for the launch and recovery of an unmanned underwater vehicle from a submarine[J].IEEE,1996.
[7]王智学.AUV回收时的运动控制方法研究[D].哈尔滨:哈尔滨工程大学,2006.
Wang Zhixue.Research on motion control method in the recovery of autonomous underwater vehicle[D].Harbin:Harbin Engineering University,2006.
Simulation of an AUV(Autonomous Underwater Vehicle)underwater recovery
DU Xiao-xu,SONG Bao-wei,PAN Guang
(College of Marine,Northwestern Polytechnical University,Xi'an 710072,China)
The three-dimensional motion model of an autonomous underwater vehicle(AUV)was built up,and the model for calculating disturbed force caused by the submarine motion was established through potential liquid theory.Then a numerical example simulating the maneuverability of the AUV underwater recovery was given.The simulation results show preliminarily that the disturbed liquid field of the submarine motion has obvious effect to the depth and the transverse displacement of the AUV,and has little effect to the pose degree of the AUV.Therefore,the AUV can complete the underwater recovery.
Autonomous Underwater Vehicle(AUV);disturbed liquid field of the submarine motion;recovery
TJ63
A
1007-7294(2011)08-0837-07
2011-01-03
国家自然科学基金(10872173)资助
杜晓旭(1981-),男,博士后,主要从事水下航行器操纵性、水下航行器流体力学和水下航行器总体设计等方面的研究。

