关于不定方程x2+4=y7
何 桃,郭金保,穆秀梅,赵杏花
(延安大学数学与计算机科学学院,陕西延安716000)
关于不定方程x2+4=y7
何 桃,郭金保,穆秀梅,赵杏花
(延安大学数学与计算机科学学院,陕西延安716000)
利用初等方法及代数数论方法讨论了不定方程x2+4=y7的整数解问题,并证明了不定方程x2+4=y7无整数解。
不定方程;整数解;整环;代数数论
设A,B∈N,A无平方因子,关于不定方程
Ax2+B=yn
为了证明我们的主要结果,需要引入下面的
引理 设M是唯一分解整环,正整数K≥2,以及α,β∈M,(α,β)=1,那么:若αβ=γk,γ∈M,则有
α=ε1μk,β=ε2νk,μ,ν∈M。
其中ε1,ε2是M中的单位元素,并且ε1ε2=εk,ε为单位元素。
证明 请参见文献[3]。
下面是本文的主要结果。
定理 不定方程

无整数解。
证明 先假设x≡1(mod2),在 Z[ i]中,(2)可写为

设δ=(x+2i,x-2i),由δ|(2x,4i)=2知δ只可能是1,1+i和2。由x≡1(mod2)知x+2i≡1(mod2),所以δ≠2。如果δ=1+i,则
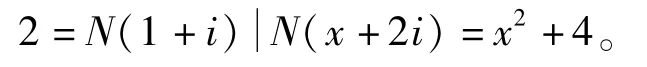
由于x≡1(mod2),因而不存在这样的整数x,y满足方程(2)。因此δ=1,由此及引理可得x+2i=(a+bi)7,x,a,b∈Z。
因而有

因此b=±1,±2。当b=1时,由第二式有
7a6-35a4+21a2-3=0,即

7a6-35a4+21a2+1=0,即
7a2,不可能。
当b=2时,
1=7a6-140a4+336a2-64,即
7a4,不可能。
b=-2时,
1=-7a6+140a4-336a2+64,即
a6-9=4a2( 5 a2-12),故也不可能。所以,此种情形无方程(2)的解。

在 Z[ i]中(3)式可写为

因此,
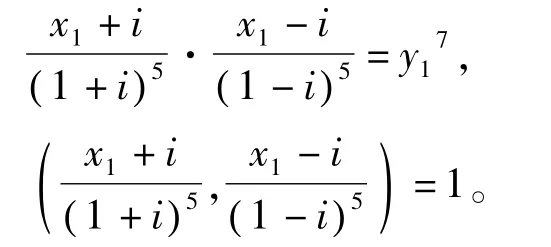
故由引理可得,
x1+i=(1+i)5(a+bi)7,即
x1=-4[a7-21a5b2+35a3b4-7ab6-b
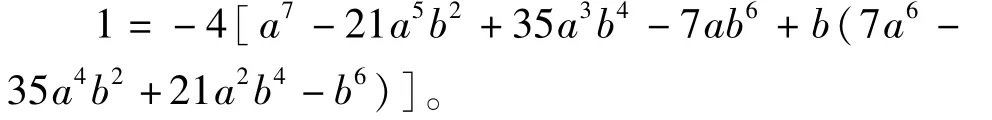
综合以上讨论情况,不定方程x2+4=y7无整数解。
[1]Lebsgue V A.Surlimpossibiliteen Numbers Entiers de E-quation xm=y2+1[M].Nouv.Amn.Math.1850.
[2]Nagell T.Sur Limpossibilite de Quelques Equations Deux Indeterminees[M].Norsk Marem Forenings Skrifter Senel,1921.
[3]潘承洞,潘承彪.代数数论[M].济南:山东大学出版社,2003.
[4]柯召,孙琦.谈谈不定方程[M].上海:上海教育出版社,1980.
[责任编辑 贺小林]
On Diophantine Equation x2+4=y7
HE TAO,GUO Jin-bao,MU Xiu-mei,ZHAO Xing-hua
(College of Mathematics and Computer Science,Yan an University,Yan an 716000,China)
Using the elementarymethod and algebraic number theory,the integer solution of the Diophantine equation x2+4=y7is discussed in this paper,and the Diophantine equation x2+4=y7which has no integer solution is proved.
diophantine equation;integer solution;integer ring;algebraic number theory
O156
A
1004-602X(2011)03-0007-02
何 桃(1984—),女,陕西榆林人,延安大学在读硕士研究生。
2011- 05- 21

