一种新型的CDMA 通信信号侦收处理中的同步算法
刘宏生
(电子工程学院电子制约安徽省重点实验室,安徽合肥 230037)
0 引言
无中心节点的无线局域网通信系统因其机动、灵活和抗摧毁性在军用和民用领域得到了越来越广泛的应用,码分多址(code division multiple access,CDMA)技术以其优越的低截获抗干扰性能在无线局域网通信系统中亦得到大量采用,如数字集群和移动通信系统。在这类CDMA通信系统中,众所周知,用户扩频码首先不可能完全正交,其次,在传输过程中,恶劣的信道也会使得扩频码的正交性严重恶化,必然会产生多址干扰、远近效应和多径效应,使得第三方在截获过程中获取用户信号同步的难度进一步加大。因此研究高性能的同步估计算法就显得非常必要。不失一般性,本文依据最为典型的民用CDMA2000系统进行截获处理过程中CDMA信号同步算法研究,该技术亦可应用到相应的电子对抗领域。
针对CDMA2000系统上行直接序列码分多址(direct sequence-code division multiple access,DSCDMA)传播链路,基于信道和时延联合估计,间接获取对目标用户信号同步的思想,具有很好的适用性[1-2]。多用户信道估计可以有效地抑制多址干扰[3-4],因此在信道和时延联合估计的同步算法中,使用多用户信道估计可以有效地提高信道估计的性能。多天线接收系统利用空间分集的思想,能够提高接收机对信号的接收能力[5]。由于多径传播信道存在角度扩展和空间选择性衰落的特性,因此在接收机中可以利用多天线空间分集的技术来提高抗信道衰落的性能,进而提高对信号的接收同步能力。并且在反向链路中,由于各用户的信号是通过不同的传播信道到达接收机,因此多天线接收系统也具有一定的多址干扰抑制能力。论文基于以上思想,提出一种多天线接收条件下信道和时延联合估计同步算法及时延估计算法,仿真表明了算法的有效性。
1 同步算法
1.1 信号模型
考虑一个K用户CDMA系统。用户k的符号序列为bk(m),经序列sk(n)扩频后的用户信号序列记为uk(n),扩频因子记为Nc,扩频序列sk(n)的周期远大于Nc,m为离散信号点数,n为扩频序列长度。用户k发射信号的等效基带形式可记为

(1)式中:Pk为用户k的发射功率因子;g(t)是发送信号的脉冲波形,由矩形脉冲通过基带滤波器得到;Tc为码片周期。
设接收机装备了Q个接收天线,设定每个接收天线间距都大于用户信号数个载波长度,因此信号到达每个接收天线的子信道可以认为是相互独立的。在每个接收天线上的接收信号都受到独立同分布的零均值高斯白噪声n(q)(t)的干扰。只要天线阵系统足够小,用户信号相对每个接收天线的传播时延都可认为是相同的。设用户k到天线q的传播信道为广义平稳非相关散射信道(wide sense stationary uncorrelated scattering,WSSUS)[6]。由于用户的发射信号是用户的信号序列与发送滤波器冲激响应的卷积,因此可以对接收信号形式作如下变换:将发射功率因子、发送滤波器、信道的冲激响应以及接收滤波器都归入到传播信道中。因此在接收机内对接收信号经过码片匹配滤波器等间隔采样后,天线q上得到的离散序列可记为
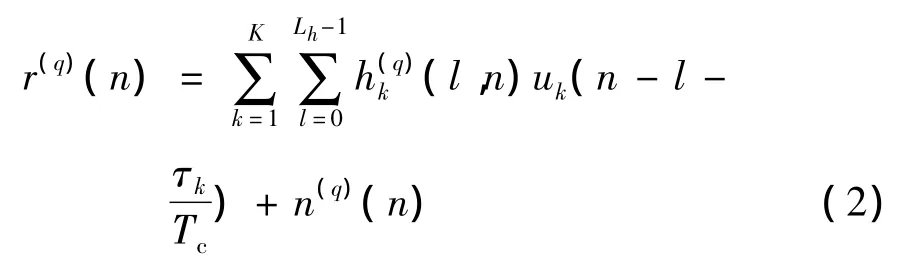
(2)式中:Lh为信道弥散长度;τk为用户k信号相对于接收机的传播时延。设常数D为一整数且满足τk≤DTc,在CDMA系统中通常有D≤Nc。在此,D可以取任意值,但是太大的D将会增加算法的复杂度,令 τk=(dk+pk)Tc,dk∈{0,1,2,…,D -1}为一整数,pk∈[0,1)为一小数。
定义Nc×(D+Lh)维扩频信号矩阵Ukm及(D+Lh)×Lh维移位矩阵Bdk

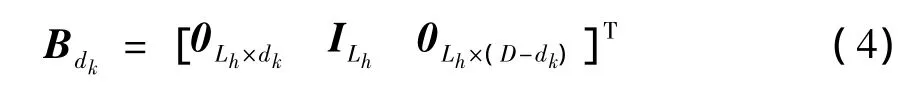
(4)式中:0Lh×dk为 Lh× dk维全零矩阵;ILh为 Lh× Lh维单位矩阵。则用户k的延时矩阵可以定义为
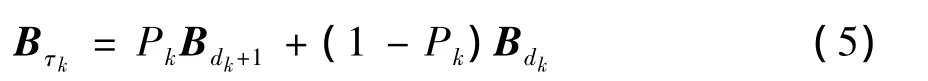
取接收采样信号观察窗长为T=NcTc,第m观察窗时隙内,天线 q接收采样信号矢量定义为设信道响应在一个观察窗时间内近似不变,则r(q)m可以表示为矩阵形式

(6)式中:h(q)km为由h(q)k得到的信道响应矩阵;n(q)m为由n(q)(n)得到的噪声分量矩阵。
进一步可得到Q个接收天线的Nc×Q维接收信号的矩阵形式为

进一步,设系统中各用户的信道弥散长度相同,均为Lh,因此,各用户的扩频信号矩阵Ukm及信道向量Fkm具有相同的维数。则接收信号矩阵形式可以更简洁地表示为

1.2 信道估计
根据建立的信号模型(11)式,信号模型是线性混叠模型。文献[3]中给出了一种最大似然估计方法,可以适用于信号模型(11)式。设用户发送长度为M的信息比特的训练序列,则可得到对信道响应和传播时延混合矩阵Fm的最大似然估计为


为减小运算量,降低对硬件资源的要求,文献[3]中同时给出了基于迭代方式的近似最大似然估计。令初始值,梯度下降法对第m个观察窗时隙按下列步骤进行迭代更新计算。

步骤4 更新信道估计值

(16)式中,μ为更新步进,μ的选取应保证算法的收敛。通过迭代的方式可以在接收完第m比特的训练序列时,迅速得到对训练序列前m个比特的近似最大似然估计。
1.3 传播时延估计
由于信道矩阵Fm中包含了用户信号的传播时延信息,通常只要获得了估计矩阵,就可以认为已经获得了对用户信号的同步,直接设计Rake或均衡接收机解调用户的信息[1],而不再需要直接估计用户的传播时延值。但在某些情况下还必须直接估计用户信号的传播时延。
用户k的传播时延τk可以分为整数dk和小数pk两部分,通常仅需要用户传播时延的整数部分值dk,就可以提取用户信道响应的有效多径分量[5]。
考查用户信道矩阵Fkm=BτkHkm的结构特性,可以得到矩阵Fkm的结构为



选取长度为Lh+1的滑动窗,计算ηkm在滑动窗内的元素的总能量为

最大能量值Rkm(n)对应位置的序号即为
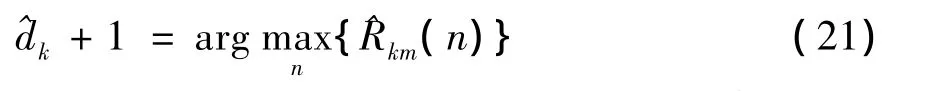

以上通过在信道估计矩阵 Fkm中截取能量窗的方法估计用户信号的传播时延,仅在用户信道估计矩阵的基础上就可以直接估计出用户的传播时延,因而可以得到较小的运算量,方法简单适用。可以将能量窗时延估计方法总结为
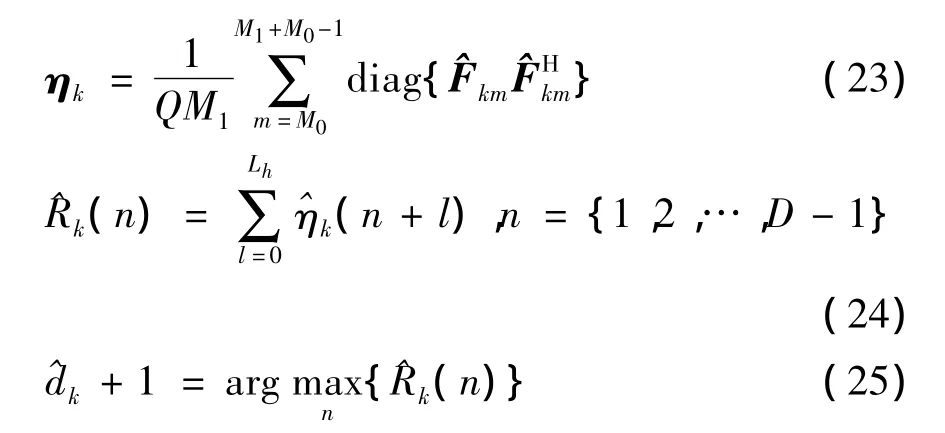
2 算法性能仿真
在下面的实验中为简单起见,依据CDMA2000系统标准,用户扩频码采用短码扩频序列,码长215,以不同的初始偏置区分各用户,扩频增益为Nc=16,设接收机有2个接收天线。信道环境为典型的城市环境,各用户相对接收机有不同的移动速度。仿真信道为Lh=5抽头的多径瑞利衰落信道,信道中的噪声是零均值的加性高斯噪声。所有用户的数据相互独立。各用户在接入系统前发送一定长度的训练序列。接收信噪比定义为目标用户接收功率与噪声功率比

(26)式中:P为目标用户的接收功率;σ2为噪声功率。
在仿真中考虑了远近效应问题,并定义信干比为

(27)式中:PI为干扰用户接收功率。
每次仿真结果的取得都是基于1 000次蒙特卡罗仿真的平均。在仿真中,设定各用户最大传播时延为D=Nc-Lh,即用户信号所有路径时延都在用户的一个信息比特时间内。
信道估计误差如图1和图2所示。
图1为2天线接收目标用户的相对信号幅度衰落曲线,目标用户信号的最大多谱勒频移为100 Hz。由于多径信道存在空间选择性衰落特性,在2个相距一定距离的接收天线上接收信号的传播子信道相互独立,在用户信号到2个接收天线的传播子信道上同时发生深衰落的概率很小,因而接收机可以获得相对较好的接收信号。显然系统装备的天线数越多所获得的空间分集增益越大。

图2为最大似然估计、梯度下降法以及滑动相关法3种信道估计方法的信道估计误差(E=‖F-F‖F)与训练序列长度的关系曲线。仿真参数设置如下:用户数K=10,SNR=0 dB,各用户接收功率相等,其中梯度下降法步进值设为μ=0.005。仿真结果表明,多用户信道估计的性能远优于单用户滑动相关法信道估计,在训练序列长达到50时,基于迭代方式的结果已基本收敛于最大似然估计结果。
图3为梯度下降法与滑动相关法的信道估计误差受噪声及远近效应影响的关系曲线。仿真参数设置如下:用户数K=5,在考虑信噪比对算法性能影响时,信噪比设置为SNR=0 dB,即各用户接收功率相等,在考虑远近效应对算法性能影响时,信干比设置为SIR=0 dB,信干比指目标用户信号相对各干扰用户接收功率比。其中梯度下降法步进值设为μ=0.005,训练序列长度为50比特。

图3 信道估计性能仿真Fig.3 Performance simulation of channel estimation
图4为时延估计算法性能仿真。在能量窗时延估计算法性能仿真中,由于能量窗时延估计算法仅估计用户信号的整数码片宽度时延,因此定义其时延估计性能为
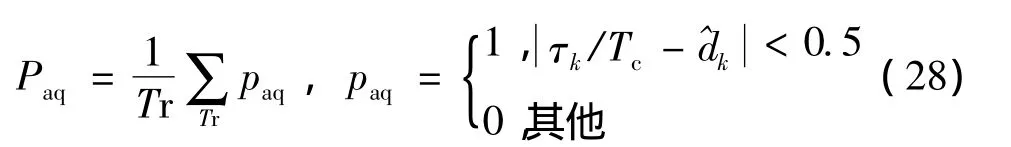
(28)式中:T r整数码片宽度时延;paq为相应码片的时延估计值;Paq为均化时延估计量。
仿真中设定系统用户为K=5。
由图4可见,时延估计算法具有良好的性能,在-15 dB信噪比或信干比条件下具有75%以上的截获概率。

图4 时延估计性能仿真Fig.4 Performance simulation of time delay estimation
3 结束语
本文利用信道和时延联合估计的思想提出一类适用于CDMA系统的多用户信号同步算法,迭代运算的方式有效地降低了算法的复杂度,使算法具有更好的适用性。在信道估计向量的基础上,本文又进一步提出一种直接估计用户信号传播时延的方法,相比信号重构的时延估计算法[7]具有简单适用的特性。多天线技术的应用使得算法具有更好的抑制多径信道衰落的能力。
另外,文中假设用户在进入系统时,发送一定长度的训练序列用作初始信道估计,这在民用通信系统IS-95和CDMA2000等移动通信系统中都是很容易满足的,在军用通信系统MSE中也可得到满足,因此具有一定的可行性和实际使用价值。
[1] TONG L,van der VEEN A J,DEWILDE P,et al.Blind decorrelating RAKE receivers for long-codeWCDMA[J].IEEE Transactions on Signal Processing,2003,51(6):1642-1655.
[2] ZHANG Y,ZHANG R.Blind MMSEmultipath combining for long-code CDMA systems[C]//IEEE.In Proceedings of IEEE International Conference on Acoustics,Speech and Signal Processing.Hong Kong:IEEE Press,2003:13-16.
[3]BHASHYAM S,AZHANG B.Multiuser channel estimation and tracking for long-code CDMA systems[J].IEEE Trans Comm,2002,50(7):1081-1090.
[4]BUZZIS,POOR H.On parameter estimation in long-code DS/CDMA systems:Cramer-Rao bounds and least squares algorithms[J].IEEE Trans Signal Processing,2003,51(2):545-559.
[5]KATZM.Code Acquisition in Advanced CDMA Networks[D].Oulu:Department of Electrical and Information Engineering,University of Oulu,2002.
[6]HOEHER P.A Statistical Discrete-Time Model for the WSSUSMultipath Channel[J].IEEE Trans On Vehicular Technology,1992,41(4):461-468.
[7]SIRBU M,KOIVUNEN V.Propagation delay estimation in asynchronous DS/CDMA using multiple antennas[C]//Soul.Proceedings of European Signal Processing Conference On Signal Processing.Toulouse:Hindawi Press,2002:653-656.

