基于级联原子库的时频原子分解
唐承志,张葛祥,荣海娜
(西南交通大学电气工程学院,四川成都 610031)
0 引言
时频原子分解是一种根据信号特点进行信号自适应分解的方法,即将信号自适应分解在一组高度冗余的过完备基(即时频原子库)上,用一系列的时频原子线性叠加来表示信号[1]。由于时频原子库是高度冗余的,分解的策略是贪婪自适应的,选取的原子具有良好时频局部特性,时频原子分解方法能够在一定精度条件下将输入信号表示成少量特征明显的信号分量,从而获得信号的稀疏表示以及自然特性[2-5]。这种信号分解方法能灵活表达信号的整体和局部结构特性,且由该方法得到的能量密度没有Wigner或Cohen类等时频方法的交叉干扰项[6]。所以,时频原子分解方法能从复杂信号和具有特殊结构的信号中提取出有用的关键信息。
由于时频原子分解方法具有以上优良特性,有学者将其用于雷达辐射源识别中,并取得了较好的效果[7-8]。但均在单一时频原子库下进行分解,某一类信号通常适合用某种原子库进行分解,而另一类信号则适合用另外的原子库进行分解;例如线性调频信号适合用Chirplet原子进行分解,常规雷达信号适合用Gabor原子进行分解。然而,雷达辐射源信号本身具有复杂、密集、多变,且交叠严重这些特点[9];在实际中就呈现为多分量雷达辐射源信号的形式,使得单一时频原子库下时频原子分解效果明显下降。因此,本文提出基于级联原子库的时频原子分解方法,用来分解多分量的雷达辐射源信号。该方法先使用 Gabor,Chirplet,Laplace 和 Damped sin 4个结构不同的时频原子库构造级联原子库,然后采用该级联原子库对多分量雷达辐射源信号进行时频原子分解。由于不同的时频原子库能稀疏的表示适合分解的那一分量信号,所以可以得到多分量雷达辐射源信号更稀疏的表示。实验结果显示,基于级联原子库的时频原子分解多分量雷达辐射源信号优于单一时频原子库下分解,能使用更少的原子来表示原信号;基于级联原子库的时频原子分解方法能更好地提取出多分量雷达辐射源信号的主要特征。
1 时频原子分解算法原理
设信号为f,其长度为N,D为过完备的原子库,g为原子库中经归一化的原子(‖g‖=1),信号分解时,在过完备原子库D中选择与信号f(t)最匹配的原子,其选择原则为内积最大,设第一个最匹配原子为g1,则

已知原子满足归一化条件,因此,信号f可以分解为2部分[2]:原子g1上的分量和残差R1f,即

接着对每次匹配的残差进行分解,直到达到终止条件,若对信号分解了n次,则可以表示成[2]
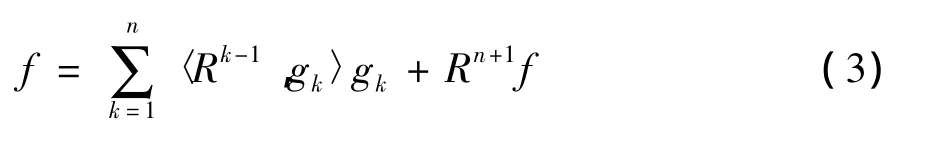
2 级联原子库(cascade-dic)
在时频原子分解算法中,常用来分解雷达辐射源信号的原子库是Gabor原子库、Chirplet原子库和Laplace原子库。这3个原子库中的原子分别具有不同的特点,适合分解不同的信号。Damped sin原子是一种典型的非对称原子库,与前面3种原子库具有不同的结构。分解后的残差通常都是非对称的,Damped sin原子适合在后面的分解中对残差进行分解。且这4个时频原子的时频图具有不同的形状。因此,本文选择这4种原子库组合来构成级联原子库。
2.1 Gabor原子库
Gabor原子由经过调制的高斯窗函数构成,定义其表达式为[2]
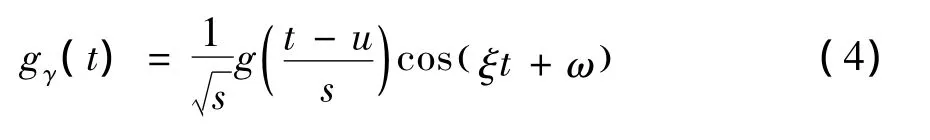
(4)式中:

参数组 γ 集合表示为 γ =(s,u,ξ,ω),其中,参数s,u,ξ,ω分别对应原子的伸缩、平移、调制频率和相位。
2.2 Chirp let原子库
Gabor原子的频率不随时间变化,在分析频率随时间变化的信号时,Chirplet原子库能更好地刻画信号的结构。Chirplet原子库是具有5个参数Gauss包络的波形集合,可表示为[8]

(6)式中:g(t)是形如 Gabor中的 Gauss窗函数;γ =(s,u,ξ,c,ω)是时频参数;s,u,ξ分别对应信号的伸缩、时间中心、频率中心;c表示信号在时频平面内的调频斜率,ω对应相位。
2.3 Lap lace原子库
Laplace原子与Gabor原子的不同处,在于其具有更平滑的窗函数。Laplace原子定义如下[1]
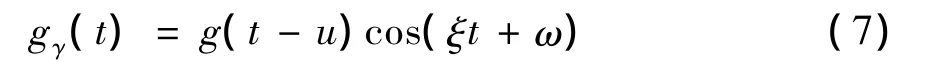
(7)式中:

参数集表示为 γ =(s,u,ξ,ω),其中,s表示原子的幅度变化;u和ξ分别表示原子的时间中心和频率中心;ω表示相位。
2.4 Dam ped sin原子库
Damped sin原子是一种典型的非对称原子。原子定义如下[1]

(9)式中:0<s≤1;U(t)为单位阶跃函数,

γ =(s,u,ξ,ω),其中,s表示原子的幅度变化;u 和 ξ分别表示原子时间中心和频率中心;ω表示相位。
3 基于级联原子库的时频原子分解方法
3.1 方法思想来源
对于任意一个多分量信号f∈RN,假设信号由n部分线性组成,则,其中,fi表示不同类型的信号。由于f包含不同类型的信号,适合分解它们的原子库类型也不同;例如f包含线性调频信号,用Chirplet原子分解能得到更好的效果,而包含常规雷达信号则用Gabor原子分解能得到更好的效果。因此使用具有不同特点的多个原子库组成的级联原子库分解它们,理应得到更好的分解效果。
3.2 基于级联原子库的时频原子分解方法实现
基本时频原子分解方法是一种贪心算法,每一次分解都需要在巨大的原子库中进行逐一的搜索,其时间复杂度极高。而其本质是一个多维参数的优化问题,已有学者将智能优化算法运用到时频原子分解参数寻优中[6]。DNA进化算法是一种基于生物DNA信息遗传机理求解复杂问题的有效算法。该算法以DNA编码为基础,利用四类碱基(A,T,G,C)对染色体进行编码,其中,A-T,G-C对应的配对关系。通过碱基的交叉、变异、选择等操作实现进化搜索[8]。该算法具有知识表达方式灵活、编码信息丰富、染色体长度可变和收敛速度快等优点[8,10]。已有学者将该算法应用在模糊控制系统设计、车间作业调度和随机整数规划问题。结果表明,算法性能大大优于传统的进化算法[8,10]。
基于级联原子库的时频原子分解方法在级联的4个原子库中搜索每个时频原子库中的最优原子,然后对搜索到的4个库中的最优原子进行比较,选择出最优时频原子。具体算法流程描述如下。
步骤1 将信号残差初始化为原信号;
步骤2 Chirpet种群初始化。随机产生一定数量的DNA链;
步骤3 进行DNA进化算法搜索Chirplet中的最优原子。主要包括选择、交叉和变异、灾变等操作,具体如下。
步骤3.1 按照DNA码表进行解码(见表1),将DNA链转化为实数;每3个碱基对应一位0到19的实数,如碱基UCA对应3,AAU对应12。再由解码后的实数映射到时频原子参数,由时频原子参数计算出种群中的每个时频原子;
步骤3.2 对种群中的每个时频原子进行适应度值评价。并保存最优原子信息;
步骤3.3 对适应度值进行排序,然后按轮盘赌规则进行选择;其后按照一定概率进行交叉和变异;
步骤3.4 判断是否进行灾变。计算种群中DNA链的多样性值,若其小于预定值则进行灾变。灾变策略为保留5%的最优个体和5%次优个体,剩下的90%个体重新初始化;
步骤3.5 重复步骤3.1直到满足终止条件。
步骤4 Gabor原子种群初始化。并按照步骤3进行最优Gabor原子搜索;
步骤5 Laplace原子种群初始化。并按照步骤3进行最优Laplace原子搜索;
步骤6 Damped sin原子种群初始化。并按照步骤3进行最优Damped sin原子搜索;
步骤7 对搜索到的4个原子进行比较,选择适应度值最大的为最优原子;
步骤8 将当前信号残差更新为原残差减去最优原子乘上最优原子与原残差的内积;
步骤9 重复步骤2直到满足分解的终止条件。

表1 DNA密码表Tab.1 DNA Code
4 仿真实验及结果
为了验证基于级联原子库的时频原子分解方法的有效性,文中使用该方法分解2个多分量雷达辐射源信号。常用的雷达辐射源信号有常规信号、线性调频、非线性调频、频率编码和相位编码等。本文中多分量雷达辐射源信号模型参考文献[11]所提出的模型,将上述5种不同类型或者同类型不同参数的单分量雷达辐射源信号进行叠加得到多分量雷达辐射源信号。其中,信号1为线性调频信号和常规信号的混合;信号2为频率编码信号和线性调频信号的混合,将这2个多分量信号使用本文方法进行分解,并与单一原子库时频原子分解进行对比。原始信号时域图如图1所示。实验所用的计算机为P4 3.0 GHz,512 MByte,仿真环境为 MATLAB7.4。本文中时频原子库的构建按照前面所描述,离散化分别按照参考文献[1]和[4]所描述。在使用DNA进化算法进行寻优时,DNA进化算法的种群大小和最大迭代次数分别为60和200,其交叉和变异概率分别为0.8和0.05。以上参数在本文方法和单一原子库时频原子分解中采用相同的设置,且都使用30个原子进行重构。为了比较2种方法,本文从重构精度、衰减率和重构信号时频能量图(time-frequency energy distribution,TFED)3个方面进行对比。重构相似度Cr定义为[3]

衰减率 Dr定义为[3]


图1 原始信号时域图Fig.1 Signal time-domain graph
表2给出了30个原子重构时的重构精度和衰减率对比。图2-3分别为重构相似度曲线和残差衰减率曲线的比较。图4-5分别给出了原始信号的时频能量图,以及基于级联原子库的时频原子分解后重构时频能量图和4个原子库分别单独分解后重构时频能量图。

表2 不同方法计算性能的比较Tab.2 Comparison of computing performances
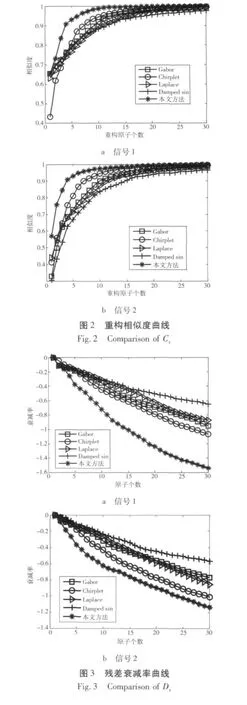
从表2可以看出,基于级联原子库的时频原子分解方法分解信号后,重构信号的相似度和残差衰减率均优于用单一原子库分解。图2-3也同样印证了这个结果,该方法分解信号后重构信号相似度和衰减率曲线一直处在优于单一原子库的位置;同样也可以看出该方法用更少的原子就能达到较高的重构相似度,能用很少的原子表示原信号。
从时频图4和图5同样可以看出本文方法的优势,图4a为信号1的原始信号时频能量图,其存在交叉项的干扰;图4b为本文方法分解后重构信号1时频能量图,其消除了交叉项的干扰,而且与后面图4c-4f相比,其时频聚集性明显好于单个原子库,且完整地刻画了信号的结构,准确地描述了信号的时频能量分布。图5a为信号2的原始信号时频能量图,其存在交叉项的干扰,而且只能大致看到该信号包含线性调频信号,无法知道另一分量信号的类型。图5b为本文方法分解后重构的时频图,从图5b中能看出该信号包含线性调频信号和频率编码信号,并能获得该频率编码信号的各个频率分量以及其大致的频率跳变点位置。图5c-5f为单一原子库分解后重构的时频图,其时频聚集性和对信号特点的描述显然不如图5b。

图4 不同方法重构信号1时频图比较Fig.4 Comparison of TFED of signal1

图5 不同方法重构信号2时频图比较Fig.5 Comparison of TFED of signal 2
由此可以知道,基于级联原子库的时频原子分解方法分解与单一原子库分解相比,分解后的原子能更好对原信号进行表示,能捕捉到能多的信息和信号的本征特征,为后面雷达辐射源信号识别提供更多的特征准备。
5 结束语
本文提出一种基于级联原子库的时频原子分解方法,该方法先构造级联原子库,然后在级联原子库中进行时频原子分解。由于级联原子库包含不同特点的原子,能适合分解不同特点的信号;且雷达辐射源信号类型未知,不同信号间交叠严重。因此本文方法比单一原子库时频原子分解方法更适合分解雷达辐射源信号。实验结果也印证了这点。使用基于级联原子库的时频原子分解方法分解多分量信号能很好的提取到信号的本征特征,为雷达辐射源信号识别提供坚实的特征准备。本文方法的计算复杂度较大,提高本文方法的效率和探索使用其它级联原子库将是进一步工作的重点。
[1]陈发宇,尚永生,杨长春.Matching Pursuits方法综述[J].地球物理学进展,2007,22(5):1466-1473.
CHEN Fa-yu,SHANG Yong-sheng,YANG Chang-chun.A general description ofmatching pursuits decomposition method[J].Progress in geophysics,2007,22(5):1466-1473.
[2] MALLAT SG,ZHANG Z F.Matching pursuits with timefrequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.
[3]朱行涛,刘郁林,徐舜,等.OFDM系统中基于匹配追踪的稀疏信道估计算法研究[J].重庆邮电大学学报:自然科学版,2008,20(1):11-14.
ZHU Xing-tao,LIU Yu-lin,XU Shun,et al.Study on sparse channelestimation algorithm base onmatching pursuit for OFDM systems[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science E-dition,2008,20(1):11-14.
[4]李映,张艳宁,许星.基于信号稀疏表示的形态成分分析:进展和展望[J].电子学报,2009,01(37):146-152.
LIYing,ZHANG Yan-ning,XU Xing.Advances and Perspective on Morphological Component Analysis Based on Sparse Representation [J].Acta Electronica Sinica,2009,01(37):146-152.
[5]JIANG Hong,WANG De-fa,LIU Chang.Joint parameter estimation of DOD/DOA/polarization for bistatic MIMO radar[J].The Journal of China universities of posts and telecommunications,2010,17(5):32-37.
[6]ZHANGG X.Time-frequency atom decomposition with quantum-inspired evolutionary algorithms[J].Circuits,Systems and Signal Processing,2010,29(2):209-233.
[7] 方纯,张葛祥,刘红文,等.快速TFAD在雷达辐射源信号中的应用[J].现代雷达,2009,31(10):64-69.
FANG Chun,ZHANG Ge-xiang,LIU Hong-wen,et al.Application of Fast Time Frequency Atom Decomposition Algorithm to Radar Emitter Signals[J].Modern Rada,2009,31(10):64-69.
[8]朱明.复杂体制雷达辐射源信号时频原子特征研究[D].成都:西南交通大学,2008.
ZHU Ming.Study on time-frequency atoms features for advanced radar emitter signals[D].Chengdu:Southwest Jiaotong University,2008.
[9] 张葛祥.雷达辐射源信号智能识别方法研究[D].成都:西南交通大学,2005.
ZHANG Ge-xiang.Intelligent recognition methoms for radar emitter signals[D].Chengdu:Southwest Jiaotong U-niversity,2005.
[10]王明春,唐万生,刘鑫,等.基于DNA遗传算法的随机整数规划期望值模型求解[J].数学的实践与认识,2009,39(4):121-126.
WANG Ming-chun,TANG Wan-sheng,LIU Xin,et al.The DNA Genetic Algorithm Applied for Solving Stochastic Integer Programming Expected Value Models[J].Mathematics in practice and theory,2009,39(4):121-126.
[11]荣海娜.多分量雷达辐射源信号模型和检测估计算法研究[D].成都:西南交通大学,2010.
RONG Hai-na.Models and detection-estimation algorithms for multi-component radar emitter signals[D].Chengdu:Southwest Jiaotong University,2010.

