适用于高阶QAM 信号的水声信道修正盲均衡算法
宁小玲,刘 忠,罗亚松,付学志,杨泗杰
(海军工程大学电子工程学院,湖北武汉 430033)
0 引言
海洋声信道在声传播过程中,由于海洋内波、湍流、温度梯度、密度分层以及其他一些引起声速局部扰动的相关现象造成了严重振幅和相位波动,以致在相干水声通信数据解调过程中造成均衡器输出信号存在相位旋转[1]。如何解决时变多途信道引起的相位旋转、提高收敛性能是提高水下通信质量亟待解决的问题[2]。不需训练序列的盲均衡算法是一种克服多途效应的有效方法,适用于带宽资源受限的水声信道,近年来一直是研究的热点[3]。传统的CMA(constantmodulus algorithm)算法性能稳定且容易实现,但CMA旨在使幅度代价函数最小化,当有相位错误时,CMA算法也会收敛,却无法完成载波恢复,需经过额外的相位恢复过程来纠正相位误差[4]。文献[5]中提出的修正的常数模算法(modified constantmodulus algorithm,MCMA)可在一定程度上进行载波相位补偿,但是MCMA算法还是存在稳态误差大、收敛速度慢等问题。文献[6]通过修正MCMA算法的误差控制函数来改善其稳态误差,同时保持了较高的收敛速度。文献[7]对CMA的代价函数进行修改,提出了适用于16QAM信号的新的载波恢复算法(new phase recovery algorithm,NCRA),纠正相位旋转,而且可以获得较低的剩余均方误差。文献[8]在MCMA代价函数的基础上,得到一种误差控制函数在CMA和DD算法间切换的、变步长的盲均衡算法,改善了常算法收敛速度慢和收敛后剩余码间干扰大的不足,能够补偿由信道引起的相位误差。
本文提出了一种适用于高阶QAM信号的水声信道改进的修正盲均衡算法(Improved MCMA,IMCMA),该算法通过对均衡器权值迭代函数进行修改,从而修正误差控制信号,有效减小对高阶信号的剩余均方误差,提高收敛速度,从而提高水声通信质量。
1 新的修正盲均衡算法
1.1 常模算法
Godard最早在文献[9]中提出CMA算法,迭代算法为


(2)式中:W(k)=[w(k),w(k-1),…,w(k-N+1)]T表示N×1维的均衡器权值向量;X(k)=[x(k),x(k-1),…,x(k-N+1)]T表示均衡器输入向量;“* ”为取共轭运算。
误差可表示为

(1)式中代价函数对相位是盲的,只能得到幅度信息,所以,尽管CMA能收敛于恒定模值,但存在相位误差。由(3)式的大量研究表明,该算法计算简单,仅比自适应最小均方误差算法(least square error,LMS)稍复杂,且该算法性能稳定,已广泛应用于水声通信中。
1.2 修正的CMA(MCMA)
针对CMA算法存在的问题,文献[5]讨论了一种修正的CMA算法(MCMA)。该算法将CM(constantmodulus)代价函数分为实部和虚部2个部分,对接收信号实、虚部分别处理,提出了一种多模准则,产生了下面的随机梯度算法

(4)式中,下标R,I分别表示相应的实部、虚部分量。算法最常用的p=2。当p≥4时,MCMA算法展现出很差的收敛性能,这是因为对于一个很小的y,(5)式的误差函数变得很小,接近于零,这时算法不能收敛[10]。p=2时得到误差函数为

(6)式中:

由(6),(7)式可知,MCMA相当与将接收信号分为实、虚部二维变量联合确定相位,适用于恒模信号(M-phase shift keying,M-PSK),也能用于QAM信号(MQAM),可在一定程度上进行载波相位补偿,但当信号相位旋转超过,误差依然难以解决[11-12]。
1.3 改进的MCMA算法(IMCMA)
观察(5)式可以看出,对于很小的y值,其误差函数变得非常小的原因是(5)式中乘积因子所致。为了解决此问题,本文对上述算法进行修改,定义一个新的权值迭代函数为

(8)式相对于(5)式没有改变其相位补偿特性,从而不影响MCMA算法克服相位旋转的能力,反而在其基础上减小了迭代过程的计算量。
相应地,误差函数变为

2 仿真试验与分析
本节采用2种M-QAM调制信号(QPSK和16QAM)通过计算机仿真研究了所提出的IMCMA算法的性能。同时与CMA算法、MCMA算法以及LMS等算法进行比较。
2.1 新算法和CMA算法以及MCMA算法比较
仿真采用如下一条具有多普勒相位旋转的典型两径水声信道[13]为

(11)式中:e-0.7j表示直达路径,其幅度为1,相移为0.7 rad;0.3e-1.8j表示幅度为0.3,相移为1.8 rad 的多径。仿真中均衡器权值向量长度21,采用中心抽头初始化,SNR=20 dB,各算法步长μ=0.000 5。
图1给出了CMA,MCMA和IMCMA 3种算法在步长μ=0.000 5时2种调制方式下的MSE(meansquare error)性能比较。由图1a和图1b可以看出,IMCMA相比MCMA和CMA算法其收敛性能均改进了很多。收敛稳定时的IMCMA和MCMA算法均方误差相当,但和CMA算法相差明显:在QPSK调制方式下,IMCMA和MCMA算法的MSE为-16 dB,而CMA约为0 dB;在16QAM调制方式下,IMCMA和MCMA算法的MSE约为-18 dB,而CMA约为-3 dB。同时可看出,IMCMA收敛速度最快,MCMA次之,CMA最慢。在QPSK调制方式下,收敛达到稳定时IMCMA(p=6)的迭代次数为2 500点,比MCMA算法约快2 500点;在16QAM调制方式下,收敛达到稳定时IMCMA(p=6)的迭代次数约为7 500点,比MCMA算法约快1×104点。可见,对于高阶QAM信号和具有多普勒相位旋转的水声信道,IMCMA相比MCMA算法和CMA算法具有优越的收敛性能,且IMCMA随参数p的增大,收敛性能逐渐增强。

图1 CMA,MCMA和Improved MMA的MSE性能比较(μ=0.000 5)Fig.1 Comparison ofmean-square error for LMS,MCMA and Improved MCMA(μ =0.000 5)
2.2 新算法在不同步长时的性能比较
仿真条件为均衡器权值向量长度21,采用中心抽头初始化;SNR=20 dB,采用16QAM调制信号。
图2给出了不同步长情况下Improved MCMA(P=6)算法MSE性能。由图2a和图2b可以看出,随着步长从μ=0.000 1逐渐增大至μ=0.001,IMCMA算法的收敛速度逐渐增快,且收敛后的稳态误差相同,在2种调制方式下分别约为 -16 dB和-18 dB。可见,在收敛稳定时,IMCMA算法具有很小的稳态误差。

图2 不同步长情况下Improved MCMA(p=6)算法的MSE性能Fig.2 Comparison ofmean-square error under different step-size for Improved MCMA(p=6)
2.3 新算法和LMS算法性能比较
由以上分析,Improved MCMA是一种具有很好相位补偿能力的盲均衡算法。目前,常用的相干水声通信中,普遍采用自适应均衡技术来克服码间干扰[2]。LMS因其结构简单,性能稳定,计算复杂度低,易于硬件实现,在水声信道均衡应用中处于绝对的统治地位[14]。为此,本文将Improved MCMA和LMS算法进行对比分析。仿真条件为均衡器权值向量长度均为21,采用中心抽头初始化;SNR=20 dB,LMS算法和Improved MCMA算法的步长均为μ=0.001。
LMS算法和Improved MCMA算法的MSE比较如图3所示。由图3a和图3b均可以看出,Improved MCMA算法相比LMS算法在达到收敛稳定时速度相对快一些,收敛后 IMCMA算法的稳态误差比LMS算法大约1 dB。LMS算法和Improved MCMA算法的输出星座图比较(16QAM)如图4所示。由图4可以看出,对于16QAM调制信号,IMCMA算法和LMS算法对相位旋转和多普勒频移都能进行很好地补偿,均衡后的星座图紧密集中,眼图张开清晰。可见,2种算法均具有良好的收敛性能。
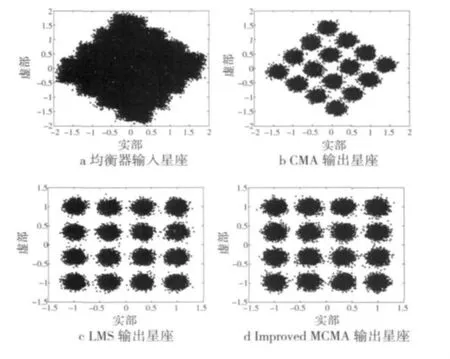
图4 LMS算法和Improved MCMA算法的输出星座图比较(16QAM)Fig.4 Comparison of output constellation for LMS and Improved MCMA(16QAM)

图3 LMS算法和Improved MCMA算法的MSE比较Fig.3 Comparison ofmean-square error for LMS and Improved MCMA
根据2种算法的特点:LMS算法具有很强的“自我调节”和“追踪”能力,但在训练过程中占用一定信道带宽;而Improved MCMA作为盲均衡算法,不需占用带宽资源,计算量小,且具有和LMS算法相当的收敛性能,所以,在高速水声通信发展的今天,Improved MCMA算法是一种非常实用的、具有发展前景的均衡算法。
3 结束语
本文提出了一种适用于高阶QAM信号的新盲均衡算法,通过具有多普勒相位旋转的典型两径水声信道进行了仿真,验证了算法对相位旋转的补偿能力以及收敛性能。新算法基于对MCMA算法权值迭代函数的分析,不削弱相位补偿能力和不增大计算量的前提下,得到一种新的权值迭代函数和误差函数。仿真结果表明,在小步长情况下,新算法相比MCMA算法在收敛速度和稳态误差上均改善了很多;在大步长情况下,相比MCMA算法收敛速度快,稳态误差相当;和LMS算法相比,两者的收敛速度和收敛后的稳态误差相差不多,且收敛后的输出星座图都紧密集中,眼图张开清晰。可见,新算法适用于高速水声通信,是一种可实用的均衡算法。
[1]STOJANOVIC M.Recent advance in high speed underwater acoustic communication[J].IEEE Journal of Oce-anic Engineering,1996,21(2):125-136.
[2] 郭业才.自适应盲均衡技术[M].合肥:合肥工业大学出版社,2007:8-9.
GUO Ye-cai.Adaptive blind equalization technique[M].Hefei:University of Hefei Industry Press,2007:8-9.
[3] KILFOYLE D B,BAGGEROER A B.The state of the art in underwater acoustic telemeiry[J].IEEE Journal of O-ceanic Engineering,2000,25(1):4-27.
[4]MATHISH.Nonlinear functions for blind separation and equalization[D].Switzerland:Swiss Federal Institute of Technology,2001.
[5] YANG J,WERNER J-J,DUMONTG A.Themultimodulus blind equalization algorithm[C]//Proc IEEE International.Conference DSP,Greece:IEEE Press,1997,1:127-130.
[6] 潘立军,刘泽民.一种适用于QAM通信系统的盲均衡算法[J].电子与信息学报,2005,27(4):663-665.
PAN Li-jun,LIU Ze-min.A blind equalization algorithm adapt to the QAM communication system[J].Journal of Electronics& Information Technology,2005,27(4):663-665.
[7] 张艳萍,郭业才,刘金铸.适用于16QAM信号的水声信道载波恢复盲均衡算法[J].系统仿真学报,2008,20(1):156-157.
ZHANG Yan-ping,GUO Ye-cai,LIU Jinzhu.Blind equalization algorithm suitable for16QAM signals for carrier recovery of underwater acoustic channel[J].Journal of System Simulation,2008,20(1):156-157.
[8] 朱行涛,刘郁林,敖卫东.一种基于MCMA的双模切换变步长的盲均衡算法[J].重庆邮电学院学报:自然科学版,2006,18(6):689-692.
ZHU Xing-tao,LIU Yu-lin,AO Wei-dong.A variable step size blind equalization algorithm for dualmode switching based on modified constantmodulus algorithm[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2006,18(6):689-692.
[9]DOMINIQUE N G.Self-recovering equalization and carrier tracking in two-dimensional data communication systems[J].IEEE Transaction Communication,1980,28(11):1867-1875.
[10] YUAN J-T,TSAI K-D.Analysis of the multimodulus blind equalization algorithm in QAM communication systems[J].IEEE Transaction Communication,2005,53(9):1427-1431.
[11]王欣,酆广增,孔媛媛.常模盲均衡算法:消除常相位偏移和多普勒频移引起的相位模糊[J].电子与信息学报,2008,30(4):848-852.
WANG Xin,FENG Guang-zeng,KONG Yuan-yuan.Blind constantmodulus algorithm:removing signal phase ambiguity generated by channel phase offset and doppler frequency shift[J].Journal of Electronics& Information Technology,2008,(30)4:848-852.
[12] ZHANG Yu-liang,WU Wei-ling,TIAN Bao-yu,et al.The Algorithm and Its Application of a Multi-Channel A-daptive Decision-Feedback Equalizer[J].The Journal of China Universities of Posts and Telecommunications,2003,10(4):59-64.
[13]王峰.基于高阶统计量的水声信道盲均衡理论与算法[D].西安:西北工业大学2003.
WANG Feng.Blind Equalization Algorithms Using Higher-order Statistics for Underwater Acoustic Channel[D].Xi'an:Northwestern Polytechnical University 2003.
[14]ISTEPANION R S H,STOJANOVIC M.Underwater acoustic digital signal processing and communication systems[M].London:Kluwer Academic publishers,2002:4-16.

